前缀和与树状数组

前缀和错题记录

Minimize the Thickness

Description

You are given a sequence a=[a_1,a_2,\dots,a_n]a=[a1,a2,…,an] consisting of nn positive integers.

Let's call a group of consecutive elements a segment. Each segment is characterized by two indices: the index of its left end and the index of its right end. Denote by a[l,r]a[l,r] a segment of the sequence aa with the left end in ll and the right end in rr, i.e. a[l,r]=[a_l, a_{l+1}, \dots, a_r]a[l,r]=[al,al+1,…,ar].

For example, if a=[31,4,15,92,6,5]a=[31,4,15,92,6,5], then a[2,5]=[4,15,92,6]a[2,5]=[4,15,92,6], a[5,5]=[6]a[5,5]=[6], a[1,6]=[31,4,15,92,6,5]a[1,6]=[31,4,15,92,6,5] are segments.

We split the given sequence aa into segments so that:

• each element is in exactly one segment;

• the sums of elements for all segments are equal.

For example, if aa = [55,45,30,30,40,10055,45,30,30,40,100], then such a sequence can be split into three segments: a[1,2]=[55,45]a[1,2]=[55,45], a[3,5]=[30, 30, 40]a[3,5]=[30,30,40], a[6,6]=[100]a[6,6]=[100]. Each element belongs to exactly segment, the sum of the elements of each segment is 100100.

Let's define thickness of split as the length of the longest segment. For example, the thickness of the split from the example above is 33.

Find the minimum thickness among all possible splits of the given sequence of aa into segments in the required way.

Input

The first line contains a single integer tt (1 \le t \le 1001≤t≤100) — the number of test cases.

Each test case is described by two lines.

The first line of each test case contains a single integer nn (1 \le n \le 20001≤n≤2000) — the length of the sequence aa.

The second line of each test case contains exactly nn integers: a_1, a_2, \dots, a_na1,a2,…,an (1 \le a_i \le 10^61≤ai≤106) — elements of the sequence aa.

It is guaranteed that the sum of nn for all test cases does not exceed 20002000.

Output

For each test case, output one integer — the minimum possible thickness of a split of the sequence aa into segments.

Note that there always exist a split, you can always consider whole sequence as one segment.

Sample 1

Input	Output
4 6 55 45 30 30 40 100 4 10 23 7 13 5 10 55 35 30 65 6 4 1 1 1 1 4	3 4 2 3

Note

The split in the first test case is explained in the statement, it can be shown that it is optimal.

In the second test case, it is possible to split into segments only by leaving a single segment. Then the thickness of this split is equal to the length of the entire sequence, that is, 44.

In the third test case, the optimal split will be [10, 55], [35, 30], [65][10,55],[35,30],[65]. The thickness of the split equals to 22.

In the fourth test case possible splits are:

• [4] + [1, 1, 1, 1] + [4][4]+[1,1,1,1]+[4];

• [4, 1, 1] + [1, 1, 4][4,1,1]+[1,1,4].

题解

#include <bits/stdc++.h> 
using namespace std;
typedef long long ll;
const ll maxn=2e3+7;
ll a[maxn],sum[maxn];

void solve()
{
    int n;
    cin>>n;
    bool is1=true;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        if(i>=2&&a[i]!=a[i-1])is1=false;//如果每个数都相等，thickness就是1了。 
    }
    if(is1)cout<<1;
    else
    {
        int minn=2023,ans;
        sum[1]=a[1];
        for(int i=2;i<=n;i++)sum[i]=sum[i-1]+a[i];
        for(int i=1;i<=n-1;i++)
        {
            if(sum[n]%sum[i]!=0)continue;
            int start=i;//start记录后续区间开始位置。 
            ans=i;//第一个区间长度是i
            int j=i+1;
            while(j<=n) 
            {
                if(sum[j]-sum[start]==sum[i])//r-(l-1)代表[l,r]区间。 
                {
                    if(j-start>ans)ans=j-start;
                    start=j;//这个区间和一样时检查下一个区间。 
                }
                else if(sum[j]-sum[start]>sum[i])break;
                j++;
            }
            if(ans<minn&&j==n+1&&start==n)minn=ans; 
        }
        if(minn==2023)cout<<n;
        else cout<<minn;
    }
}

int main()
{
    int t=1;
    cin>>t;
    while(t--)
    {
        solve();
        cout<<'\n';
    }
}

错因

忘记区间和公式是sum[r]-sum[l-1]而非sum[r]-sum[l]。

树状数组

基本结构

t[i]=sum[i-lowbit(i)+1,i]

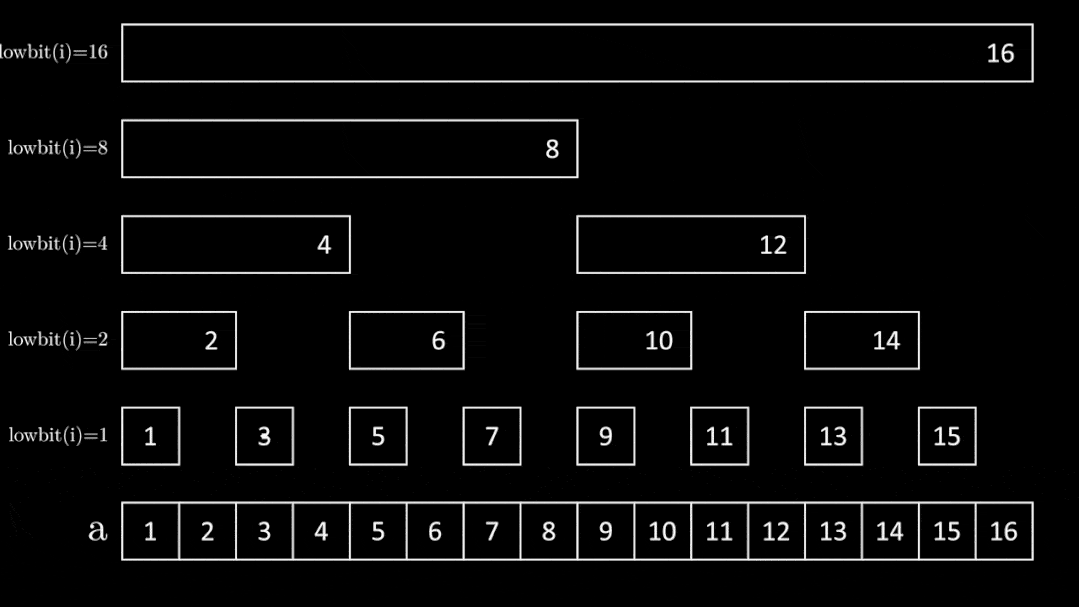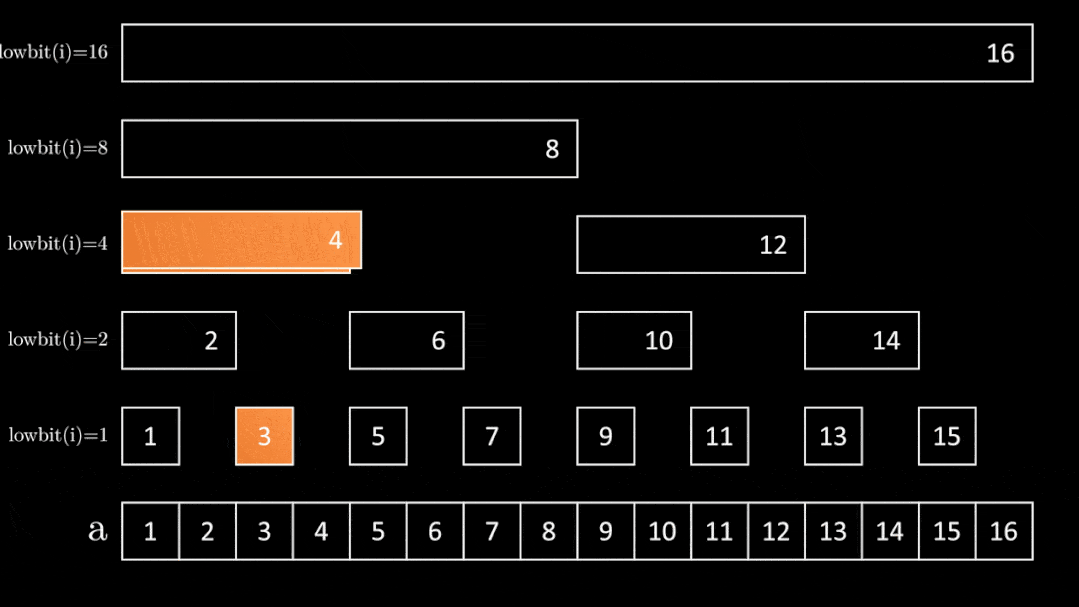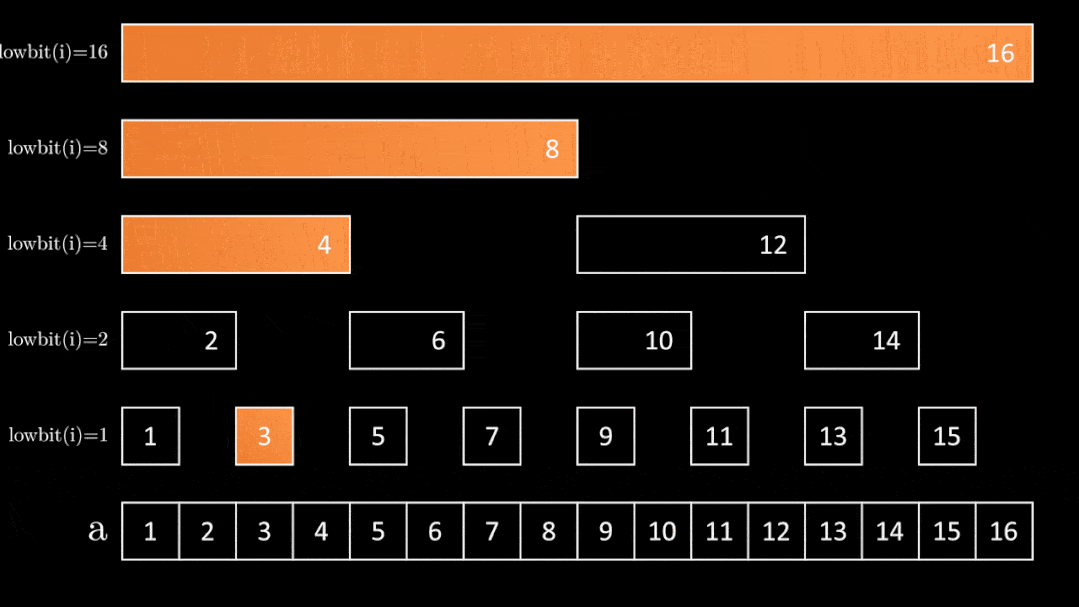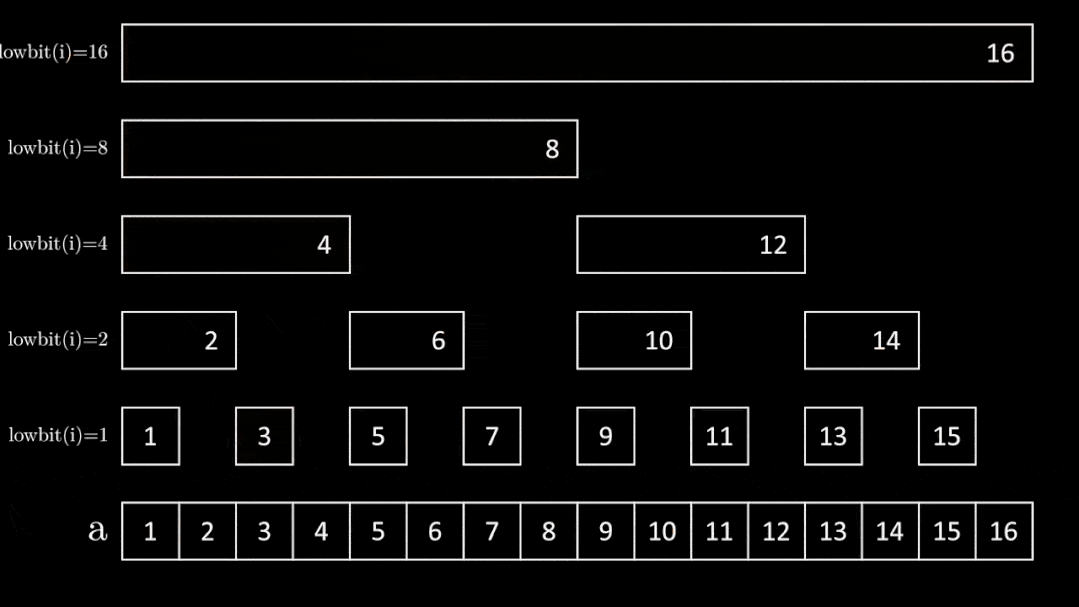
前缀和数组的获取方式

将x进行二进制拆分就可以得到表示前x项数和的前缀和数组。

int getSum(int x) {
    int sum=0;    
    while(x) {
        sum+=t[x];
        x-=lowbit(x);
    }
}

动态修改操作

每次修改a[x]必然要修改a[fa[x]]。显然fa[x]=x+lowbit(x)。

void add(int x,int val){//target[x]+=val;
    while(x<=n) {
        t[x]+=val;
        x+=lowbit(x);
    }
}