（数论十三）二项式反演

一.引出反演

​ 对于公式f(n) = g(1) + g(2) + … + g(n)，我们只要已知g(x)的函数方程，就可以得到任意的f(n)。但是已知f(x)的函数方程，我们能得到任意的g(n)吗？

​ 这时候，我们就需要用到反演定理了。利用反演定理，我们就可以通过f(x)求任意的g(n)了

二.反演定理:

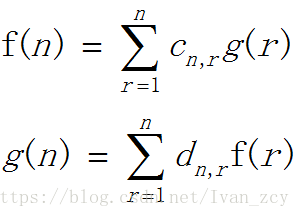
​ 对于不同的的用法，c，d是不同的，至于推导。。。我是不会，Orz～ 关于常用的反演，数学家们已经推倒出来c函数和d函数，我们直接记住用就可以了。

​ 我们常见的反演有二项式反演，斯特林反演，莫比乌斯反演和最值反演，接下来说一下二项式反演。

三.二项式反演：

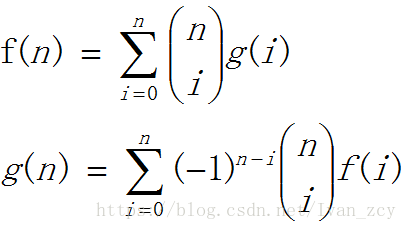
​ 其中（上:n 下:i）代表C(n, i)

​

四.例题：

​ 比如，n封信全部装错的方案数？

​ 当然啦，有个错排公式能O(n)的的推出来，我们还是先看一下二项式反演的做法：

​ 我们设g(i)代表i封信全部装错的方案数

​ 那么∑ C(n, i)✖️g(i)正好是全部的装信情况，也就是n!

​ 因此,f(n) = n! = ∑ C(n, i)✖️g(i)

​ 我们根据二项式反演公式得g(n) = ∑ (-1)^(n - i)✖️C(n, i)✖️f(i)

​ 因此我们只需要累加i从0～n的 (-1)^(n - i)✖️C(n, i)✖️(i)!的和，即为正确答案～

转载请注明出处！！！

如果有写的不对或者不全面的地方 可通过主页的联系方式进行指正，谢谢