卡尔曼滤波推导_射影定理与卡尔曼滤波-优快云博客

本文链接：https://blog.youkuaiyun.com/Int_Jarvis/article/details/83932541

本文深入探讨了卡尔曼滤波的原理与应用，通过小车模型解析了预测和测量过程，详细介绍了状态转移矩阵、控制矩阵、观测矩阵的含义及作用，同时分析了过程噪声和测量噪声对系统的影响。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

2018.11.10第一次写（像一坨屎）
2019.10.14修改
阅读了一篇论文：Comparison of Two Measurement Fusion Methods for Kalman-Filter-Based Multisensor Data Fusion，大概内容是讲基于卡尔曼滤波的多传感器融合的两种测量融合方法的比较，这篇论文里面大量的公式推导没有搞清楚，倒是把卡尔曼滤波的基础内容看了很多。以下主要记录一下查阅很多资料学到的关于卡尔曼滤波的知识（主要是讲卡尔曼滤波的思路，意义及部分推导），以后再整理一下Comparison of Two Measurement Fusion Methods for Kalman-Filter-Based Multisensor Data Fusion这篇论文的相关知识。

I.Prediction：

考虑一个在水平面向右运动的小车：

我们想要表示小车在某一时刻的状态 $x_t$ ,可以引入 $s_t$ 来表示小车在此时刻的位移， $v_t$ 表示小车此刻的速度，则我们可以用
$x_t=\begin{pmatrix} s_t \\ v_t \\ \end{pmatrix} \tag{1}$
来表示小车在t时刻的运动状态，由运动方程：
$\left. \begin{array}{l} s_t = s_{t-1}+v_{t-1}\times\Delta_t+u_t\times\frac{\Delta_t^2}{2}\\ v_t = v_{t-1}+u_t\times\Delta_t\tag{2} \end{array} \right.$
写成矩阵形式：
$\begin{pmatrix} s_t \\ v_t \\ \end{pmatrix} =\begin{bmatrix} 1 & \Delta_t \\ 0 & 1\end{bmatrix}\times \begin{pmatrix} s_{t-1} \\ v_{t-1} \\ \end{pmatrix} + \begin{pmatrix} \frac{\Delta_t^2}{2} \\ \\\Delta_t \\ \end{pmatrix}\times u_t\tag{3}$
即
$x_t=A x_{t-1}+B u_t\tag{4}$
我们把A叫做状态转移矩阵，把B叫做控制矩阵，这个矩阵表达式十分优美，只要我们建立起了小车的运动模型，表示出来A和B，我们就可以无限用上一时刻的小车状态计算下一时刻的小车状态（这是句废话，高中物理就是在把这种理想情况拿来算算算了）。然鹅，实际上，
由于风速等因素影响， $u_t$ 在每一时刻的值不可能完全切合我们想要的控制输入，这种模型不够精确造成的系统误差我们把它叫过程噪声，它是高斯白噪声（服从正态分布，纯随机过程，期望为0，方差为常数）记作 $q_t$ ，在此例中为二维列向量，对应了 $x_t$ 中两个维度的噪声，所以更为精确一点的模型应该表示为：
$x_t=Ax_{t-1}+Bu_t+q_t\tag{5}$

II.Measurement：

第III部分的校正是建立在此部分的测量的基础上的，所以我们先对测量进行阐述。还是用这个小车的例子加以说明：
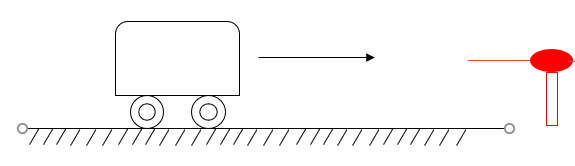
在这里插入图片描述
我们添加了一个激光测距仪，用以测量小车的位移，从而对预测模型中得到的每一时刻的预测值进行校正。
我们用 $y_t$ 表示对小车的观测状态向量，并引入一个观测矩阵来联系观测向量和小车的预测状态向量：
$y_t=C_t\,x_t+j_t\tag{6}$
$j_t$ 为观测噪声，是高斯白噪声，对应协方差矩阵 $R_t$ 。在此例中， $x_t$ 是二维列向量， $y_t$ 是一维列向量（只测距，不测速），则 $C_t$ 的形式为 $[c0]\begin{bmatrix} c & 0\\ \end{bmatrix}$ ,即：
$y_t=\begin{bmatrix} c & 0\\ \end{bmatrix}\begin{pmatrix} s_t \\ v_t \\ \end{pmatrix} \tag{7}$
所以，在 $x_t$ 形式已定的前提下，观测矩阵 $C_t$ 的形式是根据选取的观测向量的维数确定的。那么那个小c的意义又是什么呢？一般 $c$ 都取1，只是起一个映射的作用（map），即把预测的状态向量的维度映射成测量向量的维度。（注意：只是映射维度， $(7)$ 式实际上只是一个关系式，而不是说测量值是由预测值确定的！ $y_t$ 是实际中测量的值，比如传感器等数据获取设备得到的值，是真实测量到的，是多少就是多少）

上述小车模型只是为了理解卡尔曼滤波的A,B,H矩阵以及其他一些量在实际情况中具体是怎么用的。(5),(6)两个公式虽然指明了卡尔曼滤波的基本思想，即迭代求解，但还没有引入噪声协方差矩阵等量，并不是可以直接编程实现的迭代模式，下面推导卡尔曼滤波的可执行的迭代形式。为了统一起见，下文采用《An Introduction to the Kalman Filter》这篇经典论文中的公式符号进行完全体卡尔曼滤波的推导。

，，，，，，，，，，，，，，，，，，手动分割线，，，，，，，，，，，，，，，，

首先将（5），（6）公式用本文拟采用的符号进行表达：
${{x}_{k+1}}={{A}_{k}}{{x}_{k}}+B{{u}_{k}}+{{w}_{k}}\tag{8}$
${{z}_{k}}={{H}_{k}}{{x}_{k}}+{{v}_{k}}\tag{9}$
如表达式所示，A,B,H矩阵与之前的表达没有差别，用k表示离散系统时间序列更好一些，过程噪声和测量噪声数学符号改变一下。这是一个线型系统， ${w}_{k}$ 是过程噪声， ${v}_{k}$ 是测量噪声，二者是相互独立的，二者均为高斯白噪声（实际生活中大多数情况都是这样），即二者服从于均值为0的正态分布：
$p(w)\tilde{\ }N(0,Q)\tag{10}$
$p(v)\tilde{\ }N(0,R)\tag{11}$
当状态量 $x$ 是一维变量时， $w$ 和 $v$ 也是一维变量，对应的Q和R则为噪声方差，是一个数；若状态量 $x$ 是多维变量时， $w$ 和 $v$ 也是多维变量Q和R为噪声协方差矩阵，即向量的协方差为协方差矩阵，下面以噪声向量 $w$ 为例介绍一下其对应的协方差矩阵，以此引出协方差的概念：
协方差矩阵 Q（向量与向量的协方差，是一个矩阵）中的第 i 行第 j 列个元素是向量 $w$ 中的第i个元素和第j个元素（变量 $w_i$ 和变量 $w_j$ ）之间的协方差（是一个值）。对于此例来说： $x$ 有位移和速度两个分量，则向量 $w$ 也有两个对应分量 $w_1$ 和 $w_2$ ，噪声协方差矩阵 Q 为：
$Q=\begin{bmatrix} cov(w_1,w_1) & cov(w_1,w_2) \\ cov(w_2,w_1) & cov(w_2,w_2) \\ \end{bmatrix} \tag{12}$
有了以上的概念，看一下卡尔曼滤波的最终形式：
在这里插入图片描述

Table1-1 叫时间更新公式（预测），Table1-2 叫测量更新公式（校正）
各数学符号的意义如下（哈哈哈哈后面偷懒下不想码字了）：
在这里插入图片描述说一下实际中是怎么迭代求解的，根据实际系统建模， $A_k，B，Q_k，R_k, H_k$ 可以确定，（下标带k的在每个时刻都是可以变化的，但是在很多简单系统中，或者为了简化复杂系统，将这几个系统参数中的一个或几个都设置为定值。）这些系统参数确定后，要开始迭代了哈：一开始给一个 $x^k−\hat{x}_{k}^{-}$ 初始值（一般就给个0或0向量就完事了），给一个 $P_k^{-}$ （不能为0或0矩阵，若为0， $P_k$ 永远为0，永远表示估计值与真实值无误差…），一般情况下 $P_k^{-}$ 给个单位阵就可以了，会自己迭代收敛的哦。然后就开始迭代了，具体怎么迭代都不用赘述了，从这两个初始值出发看上面五个公式就能看懂了。这里顺便提一句，一般系统模型固定，其他参数可能变化不大，测量方面的 $R_k$ 的选取会较大的影响收敛速度。
参数的意义和设定都明确了，那公式图中各式的意义是什么呢，为什么就能保证这样迭代后估计值是收敛的？
下面一步一步来，首先，我们期望后验估计能够用式（1.12）那样表示成先验估计和 $(zk−Hkx^k−)({{z}_{k}}-{{H}_{k}}\hat{x}_{k}^{-})$ 的线性组合，怎么理解呢，我个人认为可以从两个方面去看待：
1.将先验估计 $x^k−\hat x_k^{-}$ 通过观测矩阵 $H_k$ 映射到观测维度上，再通过与实际的观测值 $z_k$ 作差，得到实际观测量 $z_k$ 与先验估计映射的虚拟观测量的差，这个部分其实已经是完全在观测维度上了（刚才说的映射），这也是卡尔曼滤波里面最妙的地方，把后验估计用先验估计和‘先验估计映射的测量值参与的测量差’进行线性组合，K的大小将直接决定迭代系统相信预测值 $x^k−\hat x_k^{-}$ 多一点还是相信测量值 $(zk−Hkx^k−)({{z}_{k}}-{{H}_{k}}\hat{x}_{k}^{-})$ 多一点。
2.第二层面的理解见下图右半部分，K的选取原则见下图左半部分：
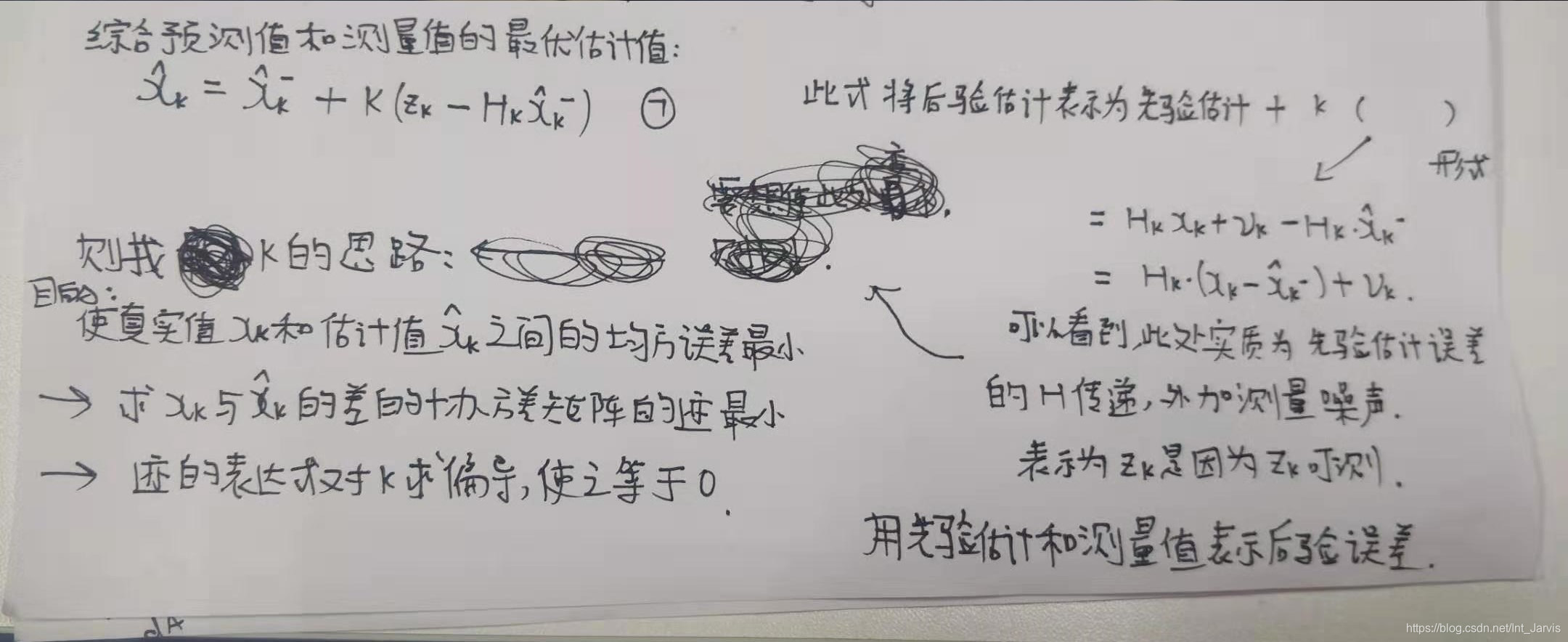在这里插入图片描述接下来推导一下 $K$ (乱码了直接放mathtype的截图吧)：
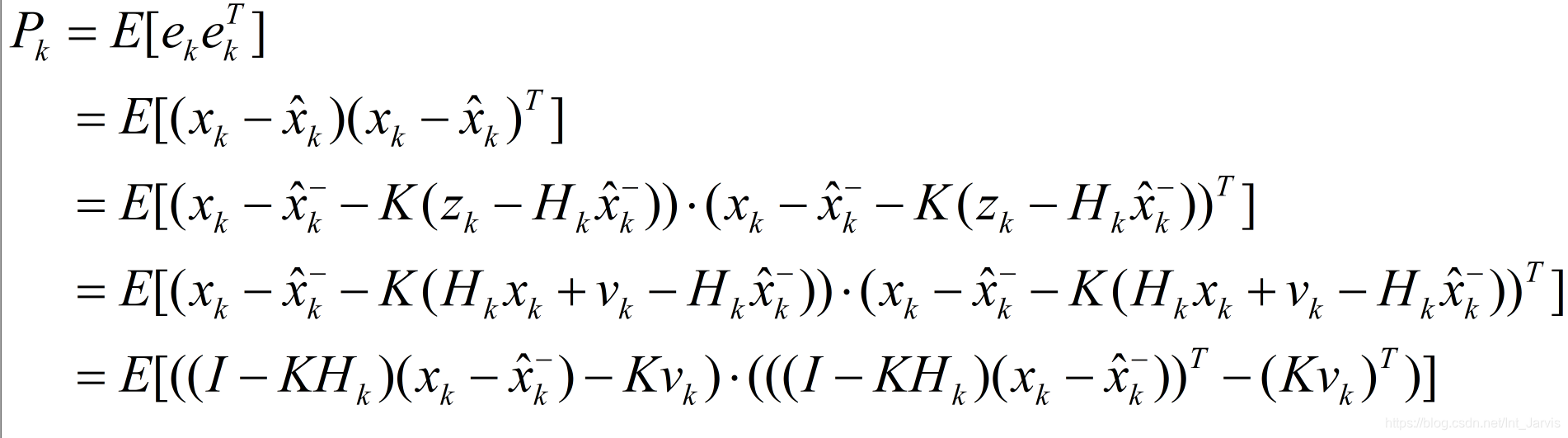在卡尔曼滤波中，我们不光希望得到状态量后验估计与先验估计的的迭代关系，还需要得到后验估计协方差矩阵与先验估计协方差矩阵之间的迭代关系。
先验估计协方差矩阵：
$Pk−=E[(xk−x^k−)(xk−x^k−)T](13) {{P}_{k}^{-}}=E[({{x}_{k}}-\hat{x}_{k}^{-}){{({{x}_{k}}-\hat{x}_{k}^{-})}^{T}}] \tag{13}$
将13代入上图中的最后一行，则有：
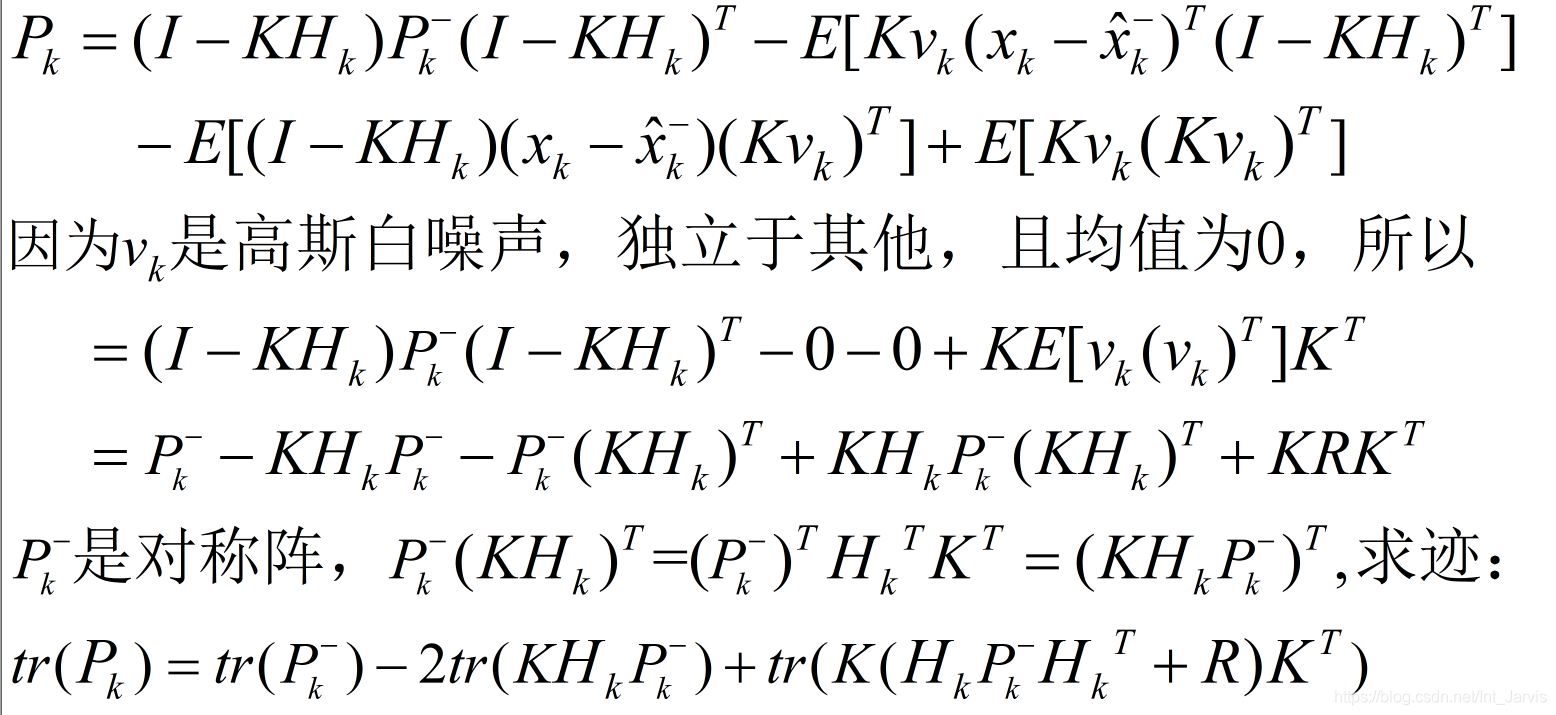
在这里插入图片描述
如之前手写分析图中所述，接下来 $tr(P_k)$ 对 $k$ 求偏导并使其等于0:
（上面几个图中的推导公式中 $K$ 就是 $K_k$ , $R$ 就是 $R_k$ ）
将这个最优的K代入 $P_k$ 得：
${{P}_{k}}=(I-{{K}_{k}}{{H}_{k}})P_{k}^{-}\tag{14}$
将式（13）展开得：
$P_{k}^{-}={{A}_{k-1}}{{P}_{k-1}}A_{k-1}^{T}+{{Q}_{k-1}}\tag{15}$
至此，所有的公式就推导完了，总结一下推导过程：
1.式（1.9）不多bb
2.式（1.12）的形式是人为构造出来的，其中K目前是未知的，此式是卡尔曼滤波得以迭代求解的关键，上面也有详细分析
3.根据上面分析的均方误差最小原则，求K，得式（1.11）
4.将这个最鸡儿棒的K代入 $P_k$ ，得到（1.13）
5.将式（13）展开即可得（1.10）