动态规划问题

选择不相邻的数（个数不限）组成最大的和，问最大是多少？

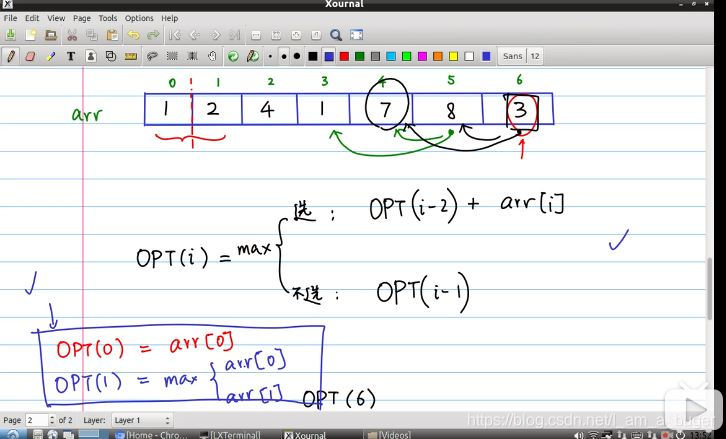
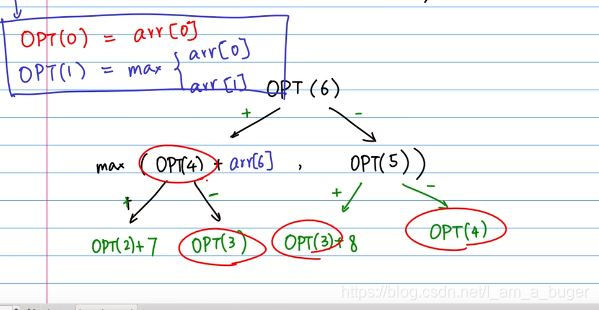
动态规划：遇到了重叠子问题，

def getMax(lis):
    import numpy as np
    s_l=len(lis);
    opt=np.zeros((s_l));
    opt[0],opt[1]=lis[0],max(lis[0],lis[1]);
    for i in range(2,s_l):
    选i：
        A=opt[i-2]+lis[i];
    不选i：
        B=opt[i-1];
    最大值赋给 opt[i]:
        opt[i]=max(A,B);
    最大值存在最后一个元素：
    return opt[s_l-1];

lis=[1,2,4,1,7,8,3]
print(getMax(lis));

15.0

问题描述为：给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最高。问题的名称来源于如何选择最合适的物品放置于给定背包中。

解决思路：动态规划，对每一件物品遍历背包容量，当背包可容纳值大于等于当前物品，与之前已放进去的物品所得价值进行对比，考虑是否需要置换。

 """
    测试数据：
    n = 6  物品的数量，
    c = 10 书包能承受的重量，
    w = [2, 2, 3, 1, 5, 2] 每个物品的重量，
    v = [2, 3, 1, 5, 4, 3] 每个物品的价值
    """
    
import numpy as np
def  knapSack(W , wt , val , n):
	初始化为0；
	opt的下标是从1(i)开始的，故wt,val小标为i-1
	opt[i][j]:表示放i之前（包括i的情况，是否放入val[i]看max）,
	容量为j的最大的价值
    opt=np.zeros((n+1,W+1),dtype=int)
    for i in range(1,n+1):
    从小到大遍历最大容量
        for j in range(1,W+1):
            if wt[i-1]<=j:
            比较当前物品放与不放;
            opt[i-1][j]:不放；
            opt[i-1][j-wt[i-1]]+val[i-1]：放
                opt[i][j]=max(opt[i-1][j],opt[i-1][j-wt[i-1]]+val[i-1]);
            else:opt[i][j]=opt[i-1][j]  ;
    print(opt);
    c=W;
    goods=np.zeros((n+1),dtype=bool)
    for i in range(n,0,-1):
    如果放入i个物品不比放i-1个物品的价值大，
    就说明 背包里没有放入第i个物品，为False;
    放入的为True
        if opt[i][c]>opt[i-1][c]:
            goods[i]=True;
            c-=wt[i-1];
    for i in range(n+1):
        if goods[i]:
            print('选择的是：',i);
    return opt[n][W];

n = 6  
c = 10 
w = [2, 2, 3, 1, 5, 2]
v = [2, 3, 1, 5, 4, 3] 
print(knapSack(c,w,v,n));


[[ 0  0  0  0  0  0  0  0  0  0  0]
 [ 0  0  2  2  2  2  2  2  2  2  2]
 [ 0  0  3  3  5  5  5  5  5  5  5]
 [ 0  0  3  3  5  5  5  6  6  6  6]
 [ 0  5  5  8  8 10 10 10 11 11 11]
 [ 0  5  5  8  8 10 10 10 12 12 14]
 [ 0  5  5  8  8 11 11 13 13 13 15]]
选择的是： 2
选择的是： 4
选择的是： 5
选择的是： 6
15