【漫话机器学习系列】098.核技巧（Kernel Trick）

最新推荐文章于 2025-04-11 09:00:00 发布

原创最新推荐文章于 2025-04-11 09:00:00 发布 · 1.1k 阅读

13 ·

CC 4.0 BY-SA版权

文章标签：

#机器学习 #人工智能

漫话机器学习系列专辑专栏收录该内容

277 篇文章

订阅专栏

核技巧（Kernel Trick）详解

在机器学习和模式识别领域，核技巧（Kernel Trick）是一种强大的数学工具，能够帮助我们在高维空间中处理数据，而不需要显式地计算高维映射。这在支持向量机（SVM）、核主成分分析（Kernel PCA）等算法中起着至关重要的作用。本文将详细介绍核技巧的数学原理、工作机制、应用场景以及其在支持向量机中的应用。

1. 核技巧的背景

在许多机器学习问题中，我们通常需要找到一个合适的函数来对数据进行分类或回归。许多算法（如支持向量机、PCA）依赖于数据点之间的内积（dot product）来进行计算。然而，如果数据具有非线性分布，则在原始空间中可能无法找到合适的线性决策边界。

问题：

线性分类器（如线性 SVM）在低维空间中难以处理非线性可分的数据。
我们可以将数据映射到更高维度，使其在高维空间中变得线性可分（如图中的映射公式）。
但直接在高维空间计算数据点之间的内积计算成本极高，尤其是当数据的维度非常高时。

解决方案：

核技巧（Kernel Trick）允许我们在不显式计算高维映射的情况下，仍然能够计算高维空间的内积。
这样，我们可以在低维空间的计算量下，利用高维空间的强大表达能力来提升分类效果。

2. 核技巧的数学原理

2.1 支持向量机的决策函数

在支持向量机（SVM）中，我们的目标是找到一个最佳的超平面来分类数据。假设数据集为：

$X = \{x_1, x_2, ..., x_n\}, \quad y_i \in \{+1, -1\}$

其中 xix_ixi 是输入数据，yiy_iyi 是对应的类别标签。

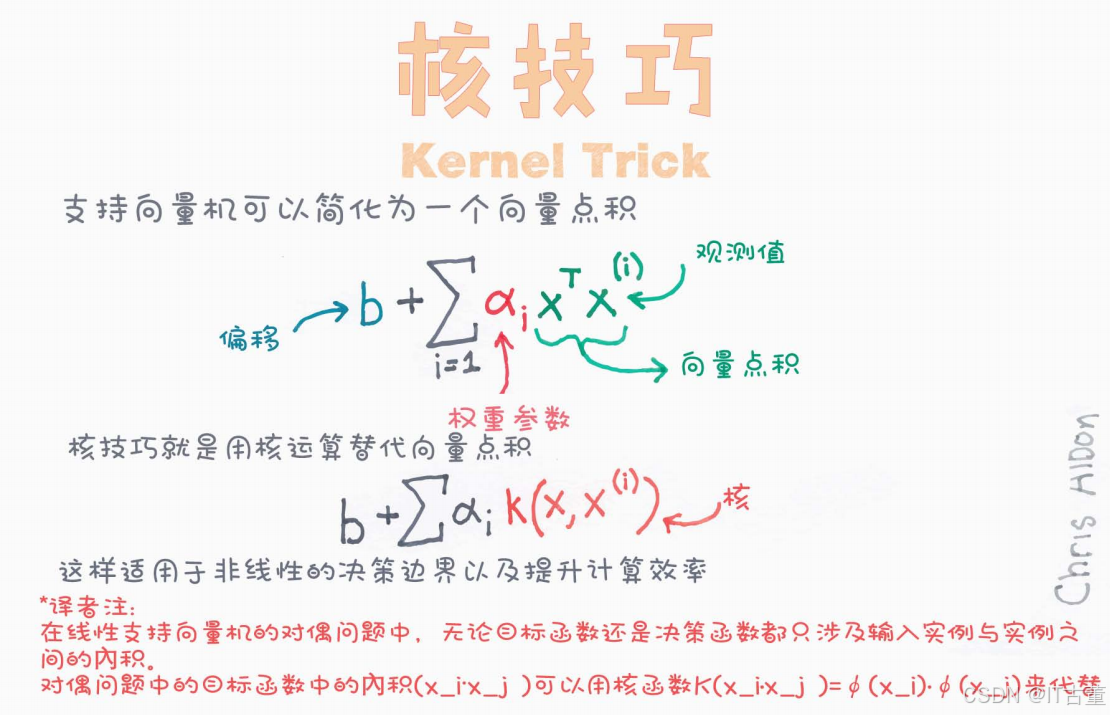
线性 SVM 的决策函数可以表示为：

$f(x) = b + \sum_{i=1}^{n} \alpha_i y_i (x_i \cdot x)$

其中：

$\alpha_i$ 是拉格朗日乘子（权重参数）。
b 是偏置项。
$x_i \cdot x$ 表示输入向量的点积（内积）。

但是，在非线性分类的情况下，数据点在低维空间中可能无法通过线性超平面分割。

2.2 核技巧的引入

如果我们希望在高维空间中执行分类，我们可以定义一个非线性映射函数 $\phi(x)$ ，将数据从原始空间映射到更高维的特征空间：

$\phi: x \rightarrow \phi(x)$

然后，在高维空间中计算点积：

$f(x) = b + \sum_{i=1}^{n} \alpha_i y_i (\phi(x_i) \cdot \phi(x))$

但直接计算 $\phi(x)$ 的维度可能非常高，甚至是无穷维，计算成本极高。因此，我们引入 核函数（Kernel Function） 来替代点积计算：

$K(x_i, x_j) = \phi(x_i) \cdot \phi(x_j)$

这样，我们不需要显式计算 $\phi(x)$ ，只需要计算核函数 $K(x_i, x_j)$ 即可。

最终，决策函数变为：

$f(x) = b + \sum_{i=1}^{n} \alpha_i y_i K(x_i, x)$

3. 常见的核函数

不同的核函数 $K(x_i, x_j)$ 对应着不同的高维映射方式。以下是几种常见的核函数：

3.1 线性核（Linear Kernel）

$K(x_i, x_j) = x_i \cdot x_j$

适用于数据是线性可分的情况，等效于不使用核技巧的情况。

3.2 高斯径向基核（RBF Kernel）

$K(x_i, x_j) = \exp\left(-\frac{\|x_i - x_j\|^2}{2\sigma^2}\right)$

该核函数将数据映射到无穷维空间，适用于大多数非线性分类问题。
σ 控制映射的尺度，较小的 σ 可能导致过拟合。

3.3 多项式核（Polynomial Kernel）

$K(x_i, x_j) = (x_i \cdot x_j + c)^d$

适用于数据具有多项式关系的情况。
c 控制偏移量，d 控制多项式的次数。

3.4 Sigmoid 核（Sigmoid Kernel）

$K(x_i, x_j) = \tanh(\alpha x_i \cdot x_j + c)$

在神经网络中常见，也被用于 SVM。
α 和 c 是超参数。

不同的核函数适用于不同的数据分布，需要根据实际问题进行选择。

4. 核技巧的应用

核技巧在多个机器学习任务中有广泛的应用，主要包括：

4.1 支持向量机（SVM）

核 SVM（Kernel SVM）可以通过核技巧处理非线性分类问题。
例如，在手写数字识别中，数据往往是非线性可分的，使用高斯核 SVM 可以显著提升分类准确率。

4.2 核主成分分析（Kernel PCA）

传统 PCA 只能处理线性降维，而 KPCA 通过核技巧，可以对非线性数据进行降维。
例如，在人脸识别中，KPCA 可以提取比传统 PCA 更有效的特征。

4.3 监督学习和聚类

核 K-means（Kernel K-means）：对非线性分布的数据进行聚类。
核岭回归（Kernel Ridge Regression）：在高维空间进行回归建模。

5. 核技巧的优缺点

优势

处理非线性问题：核技巧允许机器学习模型在高维空间中找到更好的决策边界。
无需显式映射：通过核函数计算点积，避免了高维计算成本。
适用于小样本问题：SVM + 核技巧在小样本情况下依然能取得较好的效果。

局限

计算复杂度较高：核方法需要存储和计算 n×n 的核矩阵，对于大规模数据来说成本较高。
核函数的选择：不同数据分布需要不同的核函数，选择不当可能会影响模型性能。
容易过拟合：如果核函数参数选择不当，可能会导致模型过拟合。

6. 结论

核技巧（Kernel Trick）是一种强大的数学工具，它允许我们在不显式计算高维映射的情况下，利用高维空间的特性进行分类、降维和回归。它被广泛应用于支持向量机（SVM）、核主成分分析（KPCA）、核 K-means 等算法中，使得这些方法能够有效处理非线性数据。

如果你的数据是非线性分布的，但仍然希望使用线性方法进行分类或降维，核技巧是一个值得尝试的选择！