B+树分裂与合并详解

我们来详细讲解一下 B+ 树的核心操作：分裂（Split） 和 合并（Merge）。

理解这两个操作是理解 B+ 树如何保持平衡、高效的关键。我们先快速回顾一下 B+ 树的特点，这有助于理解为什么需要分裂和合并。

B+ 树核心特点回顾

1. 多路平衡：一个节点可以有多个子节点（通常是上百个），这大大降低了树的高度。
2. 数据仅存于叶子节点：内部节点（非叶子节点）只存储键（Key） 作为导航，所有真正的数据（Data） 或指向数据的指针都存放在叶子节点中。
3. 叶子节点链表：所有叶子节点通过指针连接成一个有序链表，非常适合范围查询。
4. 严格的平衡：从根节点到每个叶子节点的路径长度相同。

为了维持这些特性，尤其是平衡性，在插入和删除操作时，节点可能会因为过满或过空而需要分裂或合并。

---

1. 分裂（Split）

分裂发生在插入（Insert） 操作过程中。当一个节点的键的数量超过了允许的最大值（通常称为 阶数 M，即一个节点最多有 M 个子节点/键），它就需要被分裂成两个节点。

分裂过程（以内部节点和叶子节点为例）

我们假设一个节点的最大容量为 M 个键（对于叶子节点，通常是 M-1 个键和 M 个指针，但为了简化，我们说 M 个元素）。当它拥有 M 个键时，就已经满了。再插入一个元素，导致它有了 M+1 个元素，此时就需要分裂。

步骤 1：定位与插入
首先，找到要插入的叶子节点，并将新的键值对按顺序插入。此时该节点有 M+1 个元素，溢出了。

步骤 2：创建新节点
创建一个新的兄弟节点（在右边）。

步骤 3：均匀分配
将原节点中 M+1 个元素平均分配到两个节点中。

• 通常，原（左）节点保留前 ceil((M+1)/2) 个元素。
• 新（右）节点接收后 floor((M+1)/2) 个元素。

步骤 4：处理叶子节点链表
如果分裂的是叶子节点，需要调整链表指针：

• 新节点的下一个指针指向原节点的下一个指针。
• 原节点的下一个指针指向新节点。

步骤 5：向上分裂（关键）
将新节点的第一个键（最小键） 提升到父节点中。

• 在父节点中，这个新键和指向新节点的指针会被插入到合适的位置。
• 注意：提升的是新节点的第一个键，而不是原节点的最后一个键。这是因为 B+ 树的内部节点键值是子节点中键值的副本，用于划分区间。

步骤 6：递归检查
将新键插入父节点后，检查父节点是否也溢出了（键数超过 M）。如果是，则递归地对父节点进行分裂。这个过程可能会一直持续到根节点。

步骤 7：根节点分裂
如果根节点发生分裂，树的高度就会增加。

• 创建一个新的根节点。
• 新的根节点包含两个键（原根节点分裂后提升上来的两个键）和两个指针（分别指向分裂后的两个节点）。

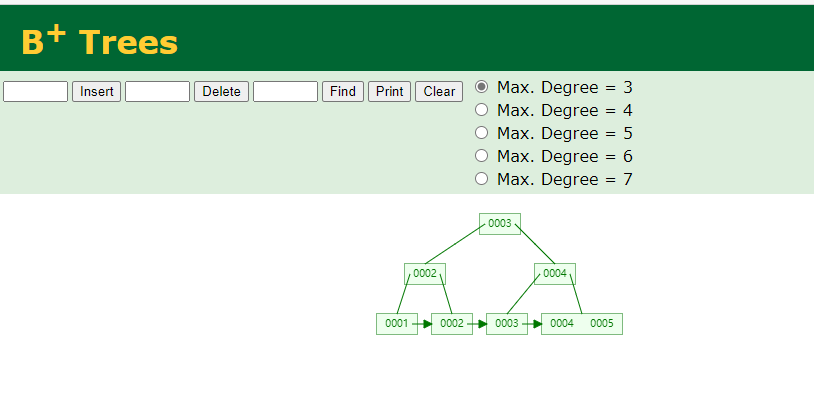
分裂示例（M=3）

假设一个叶子节点最多可存放 3 个键，现在它已经包含了 [5, 10, 15]。

• 插入 12：节点变为 [5, 10, 12, 15]（溢出）。
• 分裂：
  • 左节点：[5, 10]
  • 右节点：[12, 15]
• 调整链表：原节点（现左节点）的 next 指针指向新节点（右节点）。
• 提升键：将右节点的最小键 12 提升到父节点中。父节点现在多了一个键 12 和一个指向新节点的指针。

B+树动态演示链接