算法设计与分析: 5-25 双轨车皮编序问题

5-25 双轨车皮编序问题

---

问题描述

在一个列车调度站中，2 条轨道连接到 2 条侧轨处，形成 2 个铁路转轨栈。其中左边轨道为车皮入口，编号为 A;右边轨道为出口，编号为 D，2 个铁路转轨栈分别编号为 C 和 D， 如下图所示。编号为 a，b，…，的 n 个车皮依序停放在车皮入口处。调度室要安排各车皮 进出栈次序，使得在出口处各车皮按照预先指定的顺序依次出站。车皮移动时只能按照从左 到右的方向移动。

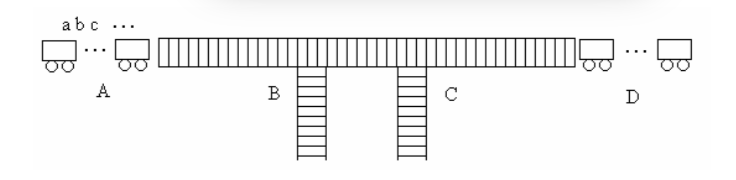
给定车皮数 n，以及各车皮的出站顺序，编程计算最优调度方案，使得移动车皮的总次 数最少。

数据输入：
第一行有 1 个正整数 n，表示车皮数。接下来的 1 行中， 是预先指定的车皮出站顺序。

---

Java

package Chapter5HuiSuFa;

import java.util.Arrays;
import java.util.Scanner;

public class ShuangGuiChePiBianXu {

    private static class Move{
        char code;
        char source;
        char target;
    }

    private static short MAXSTEPS = Short.MAX_VALUE;
    private static short MAXSHORT = Short.MAX_VALUE;
    private static short MAXLEN = Short.MAX_VALUE;

    private static Move[] solu,opt;
    private static char[] sta,stb,stc;

    private static short ks;
    private static short n,best;
    private static char[] stdd;
    private static short[] order;

    private static short count;

    public static void main(String[] args){
        Scanner input = new Scanner(System.in);

        while (true){
            ks = 0;
            best = MAXSHORT;

            n = input.nextShort();

            order = new short[n+1];
            solu = new Move[MAXSTEPS];
            opt = new Move[MAXSTEPS];
            sta = new char[MAXLEN];
            stb = new char[MAXLEN];
            stc = new char[MAXLEN];
            stdd = new char[MAXLEN];

            String str;
            str = input.next();
            char[] tmpstdd;
            tmpstdd = str.toCharArray();
            System.arraycopy(tmpstdd,0,stdd,1,tmpstdd.length);

            for(int i=1; i<=n; i++)
                for(char j='a'; j<='a'+n-1; j++)
                    if(j == stdd[i])
                        order[j-'a'+1] = (short) i;
            for(int i=1; i<MAXSTEPS; i++){
                solu[i] = new Move();
                solu[i].code = '0';
            }
            for(int i=1; i<=n; i++)
                sta[i] = (char)('a'+i-1);
            short topa,topb,topc,topd;
            topa=n; topb=0; topc=0; topd=1;
            sta[0]='0'; stb[0]='0'; stc[0]='1';
            move2(topa,topb,topc,topd,ks);
            if(best == MAXSHORT)
                System.out.println("No Solution!");
            else{
                System.out.println(best);
                output(opt,best);
            }
        }
    }

    private static void move1(short[] top){
        boolean t = true;
        while (t){
            t = false;
            if(top[4] > n){
                if(best > ks){
                    best = ks;
                    copyans(ks);
                }
                count++;
                return;
            }
            if(sta[top[1]] == stdd[top[4]]) {go('A',top,1,4,++ks); t=true;}
            if(stb[top[2]] == stdd[top[4]]) {go('B',top,2,4,++ks); t=true;}
            if(stc[top[3]] == stdd[top[4]]) {go('C',top,3,4,++ks); t=true;}
        }
    }

    private static void go(char from, short[] top,int i, int j, int ks){
            char c = ' ';
            if(from == 'A') c=sta[top[i]];
            if(from == 'B') c=stb[top[i]];
            if(from == 'C') c=stc[top[i]];

            solu[ks].code = c;
            solu[ks].source = from;
            solu[ks].target = 'D';
            top[i]--; top[j]++;
    }

    private static void copyans(int k){
        for(int i=1; i<=k; i++){
            opt[i] = new Move();
            opt[i].code = solu[i].code;
            opt[i].source = solu[i].source;
            opt[i].target = solu[i].target;
        }
    }

    private static void move2(short topa2, short topb2, short topc2, short topd2, short ks2){
        short tp,ks1;
        short topa,topb,topc,topd;
        short[] top = new short[5];
        char[] gb2,gc2;
        top[1]=topa2; top[2]=topb2; top[3]=topc2; top[4]=topd2; ks=ks2;
        move1(top);
        topa=top[1]; topb=top[2]; topc=top[3]; topd=top[4];
        gb2 = Arrays.copyOf(stb,stb.length);
        gc2 = Arrays.copyOf(stc,stc.length);
        ks1 = (short) (ks+1);
        for(tp=1; tp<=3; tp++)
            switch (tp){
                case 1://a-->b
                    if(topa > 0){
                        solu[ks1].code = sta[topa];
                        solu[ks1].source = 'A';
                        solu[ks1].target = 'B';
                        stb[++topb] = sta[topa--];
                        move2(topa,topb,topc,topd,ks1);
                        stb = Arrays.copyOf(gb2,gb2.length);
                        stc = Arrays.copyOf(gc2,gc2.length);
                        topa++; topb--;
//                        ks=(short) (ks1-1);
                    }
                    break;

                case 2://a-->c
                    if(topa>0 && ord(sta[topa])<ord(stc[topc])){
                        solu[ks1].code = sta[topa];
                        solu[ks1].source = 'A';
                        solu[ks1].target = 'C';
                        stc[++topc] = sta[topa--];
                        move2(topa,topb,topc,topd,ks1);
                        stb = Arrays.copyOf(gb2,gb2.length);
                        stc = Arrays.copyOf(gc2,gc2.length);
                        topa++; topc--;
//                        ks=(short) (ks1-1);
                    }
                    break;

                case 3://b-->c
                    if(topb>0 && ord(stb[topb])<ord(stc[topc])){
                        solu[ks1].code = stb[topb];
                        solu[ks1].source = 'B';
                        solu[ks1].target = 'C';
                        stc[++topc] = stb[topb--];
                        move2(topa,topb,topc,topd,ks1);
                        stb = Arrays.copyOf(gb2,gb2.length);
                        stc = Arrays.copyOf(gc2,gc2.length);
                        topb++; topc--;
//                        ks=(short) (ks1-1);
                    }
                    break;
            }
    }

    private static short ord(char c){
        if(c == '0') return 0;
        if(c == '1') return 100;

        return order[c-'a'+1];
    }

    private static void output(Move[] opt, int best){
        for(int i=1; i<=best; i++)
            System.out.println(opt[i].code+" "+opt[i].source+" "+opt[i].target);
    }
}

---

Input & Output

3
abc
5
c A B
b A B
a A D
b B D
c B D


10
adbcegfjhi
19
j A B
i A C
h A C
g A B
f A C
e A B
d A B
c A C
b A C
a A D
d B D
b C D
c C D
e B D
g B D
f C D
j B D
h C D
i C D

---

Reference

王晓东《计算机算法设计与分析》