文章总结:
问题:
- 交通数据的非欧几里得结构
- 复杂的空间相关性和动态的时间依赖性
- 没有捕捉到不同时间段内多个节点之间的依赖关系
- 现有的工作大多只基于流量节点之间的距离生成浅层图,降低了它们捕捉复杂相关性的能力
介绍:
定义:根据道路上的历史交通数据来预测未来的交通网络状况。
挑战性:
由于数据的非欧几里得结构、复杂的空间相关性和交通模式的动态时间依赖性
- 空间和时间相关性之间的干扰
- 交通模式通常是每天或每周周期性的
- 每日数值显示了高峰和非高峰时段的拥堵变化模式,每周数值显示了工作日和周末的流量波动模式
以往研究:
多变量时间序列(MTS) 包括多个与时间相关的变量,每个变量依赖于其早期的值以及来自其他相关变量的值(即,道路网络中任何节点的未来交通不仅依赖于其历史交通,还依赖于网络中的其他节点)
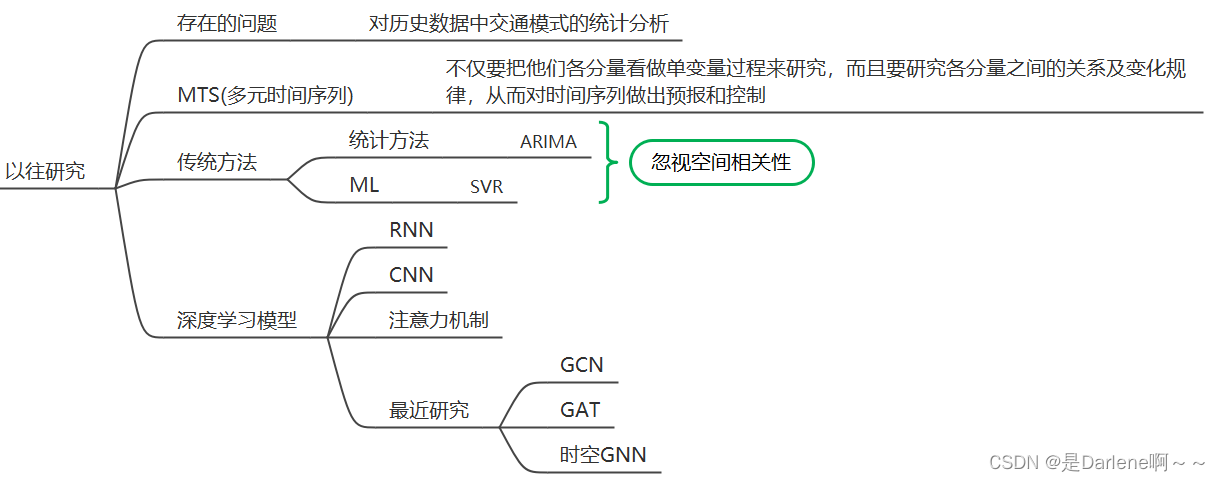
关于GAN:
- 大多采用具有限制表示的浅图,这往往限制了它们导出复杂关联的能力
- 相似地处理整个节点,从而忽略了路网拓扑结构的可变性质
- 忽略了不同时间间隔内不同节点之间的依赖关系
贡献:
- 提出了一种基于不同视角的多GCN模型来学习交通节点之间的空间相关性
- 利用GRU和自注意力来提取时间相关性
- 设计对抗训练策略,通过将无监督训练和有监督训练结合起来,以共同受益的方式提高模型的学习能力。
背景
生成对抗网络
无监督学习模型

方法

道路节点相似性:DTW方法
相关性:RobustSTL算法:节点流量数据分解为趋势性和季节性。 皮尔逊相关系数计算各分量之间的相关性。
通过计算节点间的距离来丰富空间信息。
补充:
- RobustSTL算法
一种用于时间序列分解的算法,它可以将时间序列分解为趋势、季节性和残差三个部分。使用局部加权回归(Loess)方法来估计趋势和季节性分量,然后通过减去趋势和季节性分量得到残差。其中,局部加权回归是一种非参数回归方法,它将每个数据点周围的邻近点作为训练数据来估计该点的回归值,从而得到平滑的估计结果。
- 局部加权回归:
对于趋势分量,可以使用LWR对时间进行回归,将时间作为自变量,将原始数据作为因变量,通过不同的带宽参数(bandwidth)进行拟合,得到趋势分量的估计值。
对于季节性分量,可以将季节指标(seasonal index)作为自变量,将原始数据作为因变量,同样通过LWR进行回归拟合,得到季节性分量的估计值。
- DTW
DTW(Dynamic Time Warping)是一种用于比较两个时间序列之间的相似性的方法。在将两个时间序列进行对齐的过程中,允许其中一个时间序列相对于另一个时间序列发生一定的延迟或压缩,以使它们之间的距离最小化。
- 皮尔逊相关系数
皮尔逊相关系数(Pearson Correlation Coefficient)是一种用于衡量两个变量之间线性关系强度的方法。它的取值范围在-1到1之间,其中取值为-1表示完全负相关,取值为0表示没有线性关系,取值为1表示完全正相关。
邻接矩阵构造
相似邻接矩阵ASIM

稀疏动态时间规整
相关邻接矩阵ACOR
在时间序列分解中: 第一种是趋势,它反映了数据的共同趋势,包括三种不同的类型:下降趋势、上升趋势和不变趋势。 第二个是季节性,这是一个反复出现的、可预测的特征。

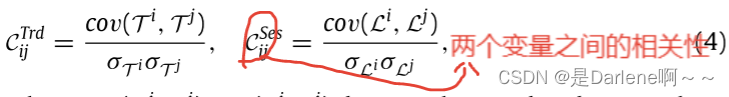
趋势相关性和季节相关性;相关邻接矩阵是趋势邻接矩阵和季节邻接矩阵的Hadamard product (⊙)
距离邻接矩阵ADST

生成对抗网络:
使用多个图来捕捉节点之间复杂的时空依赖关系:
利用GCN-SIM模型从相似度方面对图节点之间的关联进行建模和提取。
ACOR与节点在给定时间窗内的时间序列数据一起传递到相关图(GCN-COR)中
将前面的图集成为一个综合图(GCN-SYN)。 这种图的重要性来自于它能够捕获节点之间的全局依赖关系,并对任何单独的图都无法建模的隐式关联进行建模。
自注意力机制的优点在于,对序列中的每个元素计算出一个权重向量,用于表示该元素与序列中其他元素的相关性它能够学习到不同位置的信息之间的关系,而不是像传统的循环神经网络那样只能捕捉到相邻位置之间的关系
GRU是一种门控循环单元

TFGAN中的鉴别器以两组样本作为输入,其目的是确定哪一个样本是真的,哪一个样本是假的。
对抗性训练:许多流量预测模型的目标是最小化一个特定的损失函数,如MSE损失。 然而,在现实世界的流量不确定性中,一个执行步进精度的损失函数是不能胜任的,从而导致性能不佳。 为了克服这一问题,我们提出了一种将对抗性损失和MSE损失相结合的对抗性训练过程。 在对抗性训练中,我们的模型将能够学习真实数据的分布,因此它的预测将尽可能接近真实数据。 在有监督的训练过程中,我们的模型能够提取交通节点之间的时空关系,从而最大限度地减少预测与实际数据之间的MSE损失























 2084
2084

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








