统计基础（十一）逻辑回归与无参数回归

𝐋𝐨𝐠𝐢𝐬𝐭𝐢𝐜 𝐑𝐞𝐠𝐫𝐞𝐬𝐬𝐢𝐨𝐧 and Non-parametric Regression

1.知识点回顾

1.1 F测试

F测试有两种类型:

• 整体F检验——检验模型的有用性
• 部分F检验——检验线性约束
  

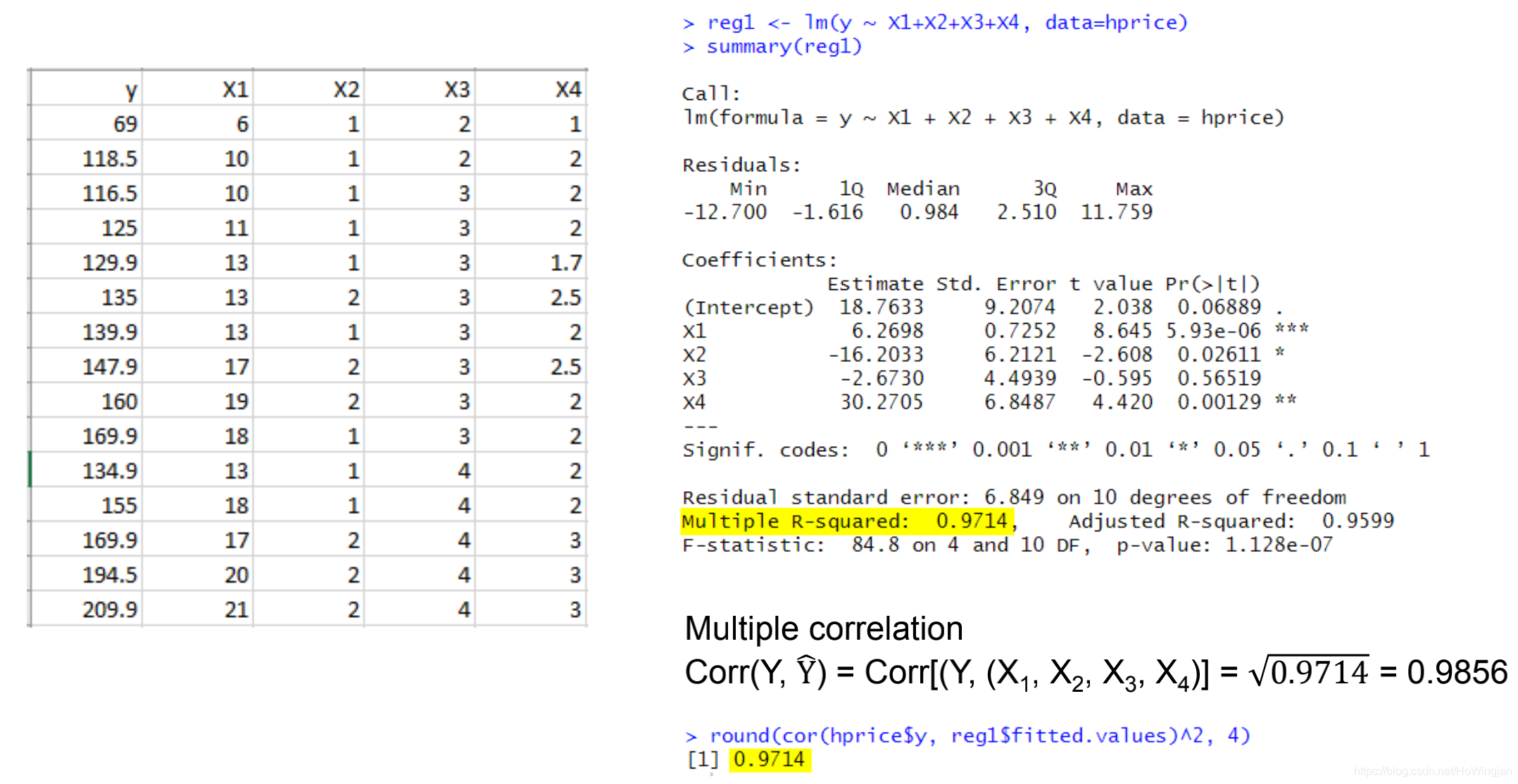
1.2多项R^2和多项R

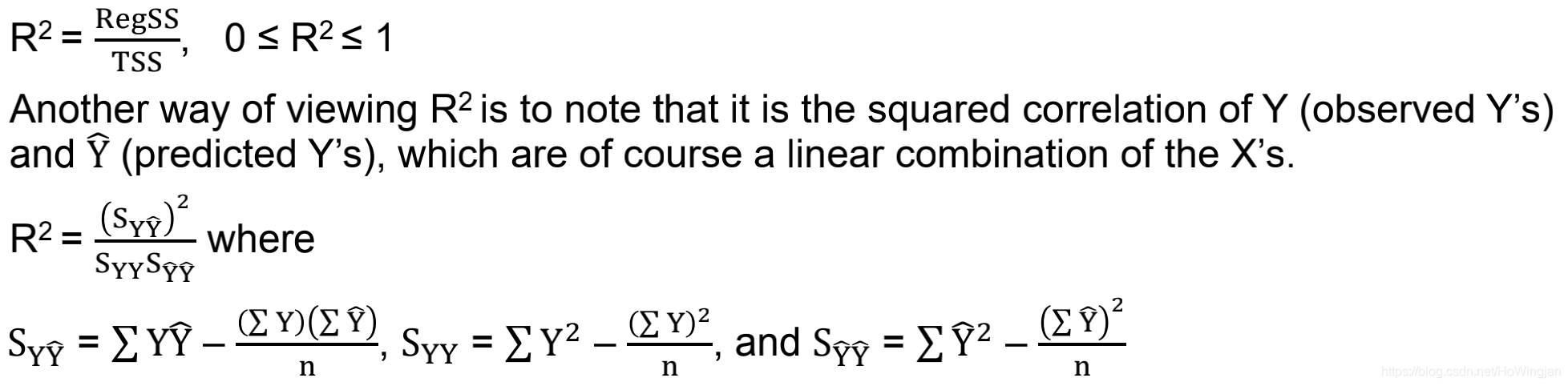
R^2的正平方根等于r。与r不同的是，r可以取正值也可以取负值，r可以从0变化到1。R的值越接近1，自变量与因变量之间的线性关系越大。
▪R = 1表明预测是完全正确的。
▪R = 0表明自变量的线性组合不优于因变量的固定均值。

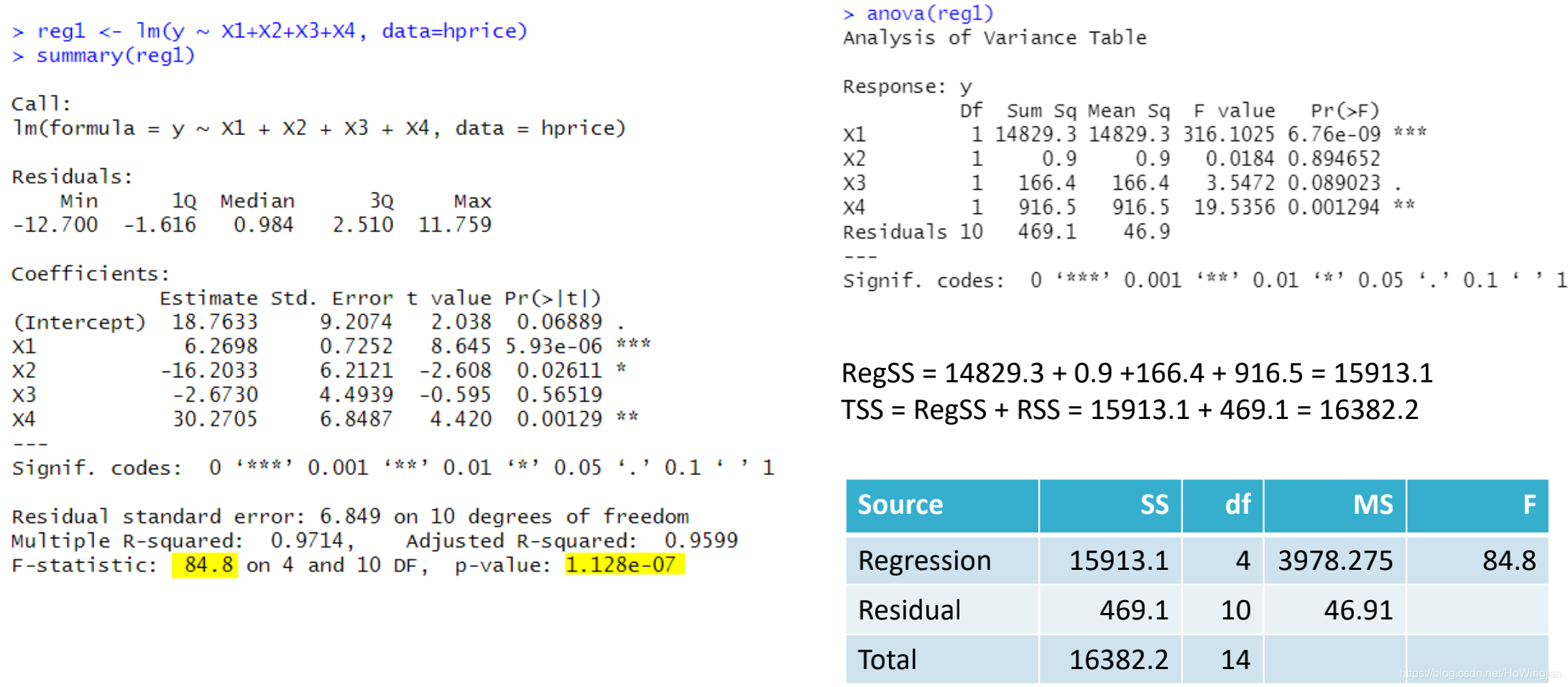
1.3 anova表

2.线性概率模型LPM

• 到目前为止，我们一直假设因变量是连续的(例如数量、价格等)。
• 然而，许多选择不能用连续变量来衡量。如:上不上大学;买房子或租房子;批准或不批准贷款申请;投不投工党等。
• 我们想要解释为什么做出这样的选择，哪些因素进入了决策过程，以及每个因素对结果的影响有多大。有时我们想预测这样的选择。
• 这样的选择导致模型中因变量Y在本质上是二元的(即等于0或1)。
• 在Y连续的模型中，我们的目标是在给定回归变量值的情况下估计其预期值或平均值;例如，我们想要E(Y | X1, X2，…，Xk)，其中X可以是定性的或定量的。
• 在Y为二进制的模型中，我们的目标是估计发生某事的概率;即P(Y = 1 | X1, X2，…，Xk)。因此，二元响应回归模型通常被称为概率模型。

▪我们首先考虑二元响应回归模型。有三种方法来开发一个二进制响应变量的概率模型:

• 线性概率模型(LPM)
• logit模型

2.2 线性概率模型(LPM)

▪考虑$Y_i={\beta }_0+{\beta }_1{X}_1+{\epsilon }_i$

• X =家庭收入
• 有房子的家庭Yi = 1，没有房子的家庭Yi = 0
• ε是一个随机误差，E(ε|X) = 0
  ▪由于因变量模型的二元性质(1)被称为线性概率模型(LPM)
  ▪令Pi 为 Yi = 1的概率，(1−Pi) 为 Yi = 0的概率。
  ▪因此，Yi遵循$E(Y_i)=P_i=P(Y_i=1)$的伯努利概率分布

Non-normality的随机误差ε𝐢

▪假设εi正态分布是对于LPMS是站不住脚的，像Yi的随机误差只有两个值
▪如果我们将模型改写为:εi = Yi -β0 - β1xi，则εi的概率分布为

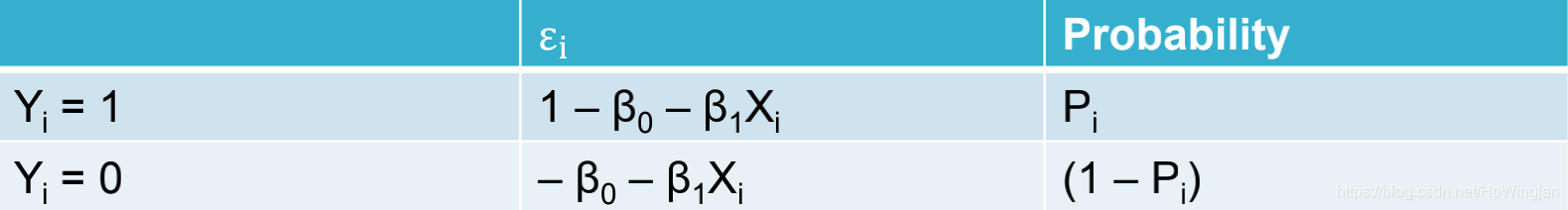
因此，不能假定εi是正态分布的。相反，它们遵循伯努利分布。
▪不履行正态性假设有那么重要吗?

• 我们知道OLS点估计仍然是无偏的。
• 当样本容量无限增加时，OLS估计量趋向于正态分布
• 因此，在大样本中，LPM的统计推断将在正态假设下遵循通常的OLS程序

扰动的异方差

▪在LPM中，随机误差是同方差的，这已经不能再维持下去了。
▪误差项(服从伯努利分布)的方差为:$Var({\epsilon }_i)=P_i(1-$