统计基础（二）概率

Probability

1.名词解释

Experiment 实验
获得观察、结果或简单事件的过程
Sample point 样本点
实验最基本的结果
Sample space 样本集合
所有样本的集合

Mutually Exclusive 互斥
两种结果不可能同时发生
eg.一个人不可能既是男性又是女性
Collectively Exhaustive集体
样本空间中的一个结果必须出现，事件集覆盖了整个示例空间
eg.男性和女性

Simple event 简单事件
一个特征的结果
Compound event 复合事件
两个或多个事件的组合
联合事件是一种特殊情况:两个事件同时发生

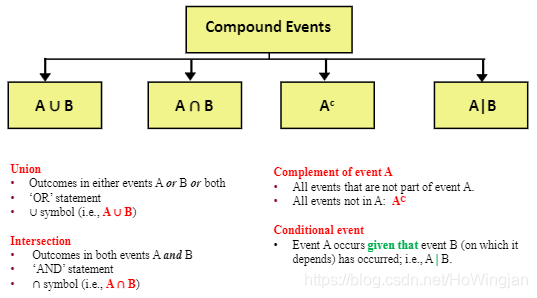
2.可视化

Contingency Tables 列联表

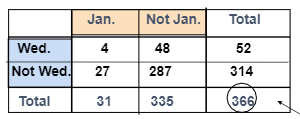
Decision Trees 决策树

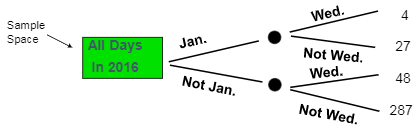
Venn Diagram 韦恩图

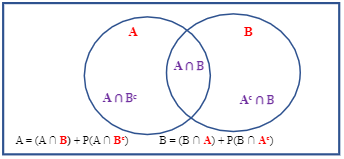
3.两种概率

Data-based (frequentist) probability

•这是对概率的经典解释。
•一个事件发生的概率是该事件在大量重复实验(模拟)中发生的次数的比例。
•在某些方面，主观概率是频率概率的非正式版本，使用个人的历史和经验(“个人数据”)作为基础
•例如，抛1万次硬币，计算正面出现的频率。

Model-based (theoretical) probability

•事件的概率是基于上下文的模型。这是一个数学结构，为每一个可能的事件分配一个数字。
•2种抛硬币模式:

• 确定性物理模型Deterministic physics model:硬币落地的方向是由许多复杂的因素决定的，比如它从哪条路开始向上程度旋转，它离开拇指时的速度和角度，以及它要下落的距离。
• 统计概率模型Statistical probability model:投掷一枚均匀硬币，有一半的概率是正面和反面，其顺序不可预测(随机)。
  举例：投掷一枚均匀的硬币:在抛硬币有两种结果的前提下，投掷一枚均匀的正面的概率为0.5

4. 概率的基本原则

补充规则：
P(A) = 1 – P(A^c)
加法规则-找出事件并集的概率
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
乘法法则-找出交集事件的概率
P(A ∩ B) = P(A|B)*P(B)
P(A ∩ B) = P(B|A)*P(A)

互斥事件
两个事件在同一次试验中不可能同时发生
P(A ∩ B) = 0
P(A ∪ B) = P(A) + P(B)
独立事件
一个事件的发生不影响另一个事件的发生
P(A ∩ B) = P(A)P(B)
P(A|B) = P(A) or P(B|A) = P(B)

贝叶斯公式

$$P(B_i|A)=\frac{P(A|B_i)P(B_i)}{P(A|B_1)P(B_1)+P(A|B_2)P(B_2)+...+P(A|B_k)P(B_k)}$$
例子1

5.随机变量

随机变量是指其数值由随机试验的结果决定的变量。

随机变量的类型:

离散型随机变量

随机变量的取值是有限的。
概率质量函数probability mass function

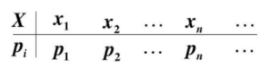
连续型随机变量

随机变量X的所有可能取值不可以逐个列举出来，而是取数轴上某一区间内的任一点的随机变量。
概率密度函数probability density function

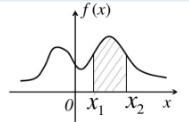
6.分布的种类

我们可以用两种方式描述分布:

背景

• 总体分布:就是一个概率分布。
• 样本分布:从总体中随机抽取的一个子集。其中，样本具有和总体相同的分布，样本之间两两独立。
• 抽样分布(统计ഥX):我们可能兴趣估计从这个样本均值。我们可以进行另一项研究取另一组样本计算样本均值。重复这样做就能得到样本均值的抽样分布。

基本性质:

• 离散分布Discrete distribution
• 连续分布Continuous distribution

7.计数技巧

乘法运算规则

如果做一件事有m种方法，做另一件事有n种方法，那么两件事都有m*n种方法。

排列Permutation

排列是一组对象的排列，其中有第一、第二和第三个顺序n;也就是说，顺序很重要。{a, b}与{b, a}不同。
排列有以下两种类型:
无重复：$${}_n{P}_r=\frac{n}{n-r!}$$

有重复：$${}_n{P}_r=n^r$$

组合Combination

一组对象的组合是不考虑其顺序的对象的子集;也就是说，顺序并不重要。{a, b}与{b, a}相同。
有以下两种组合:
无重复：$$\frac{n!}{r!(n-r)!}$$
有重复：$$\frac{(n+r-1)!}{r!(n-1)!}$$