【算法】树状数组

更好的观看 ：链接

树状数组和线段树的区别：

• 线段树可解决的题目多

• 树状数组代码短，常数很小

[]
[]

树状数组

1. 特点：可以动态、快速地求前缀和。

2. 时间复杂度：O(log n)。

3. 原理

树状数组是1维表示(为了清楚，才划分的层次)

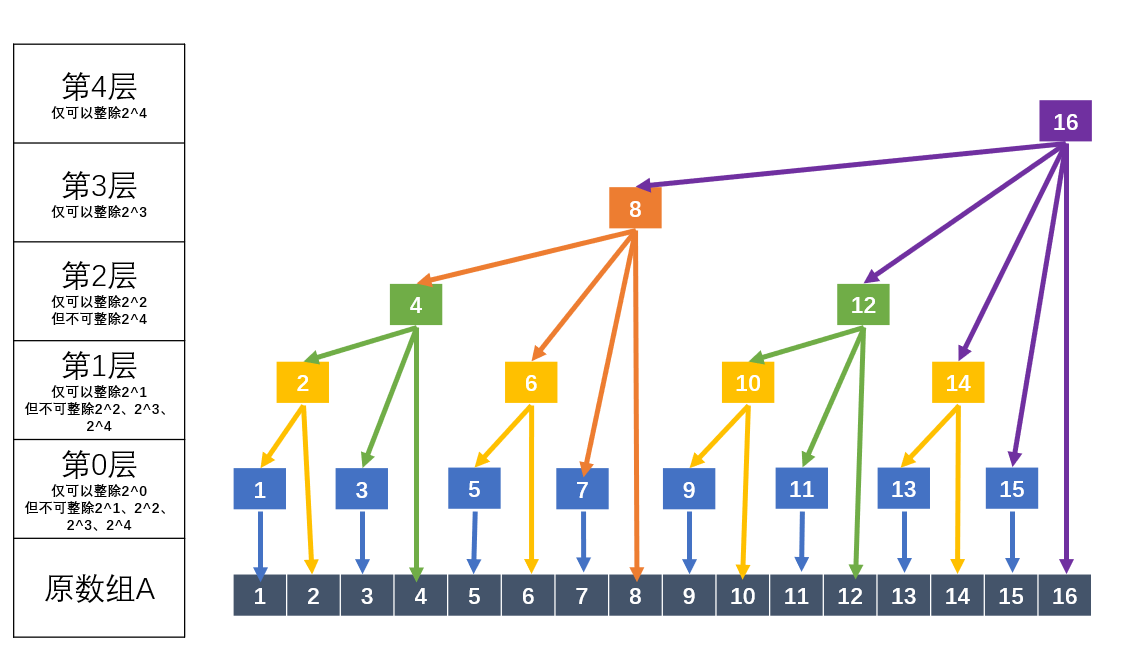
c[1] = a[1]
c[2] = c[1] + a[2] = a[1] + a[2]
c[3] = a[3]
c[4] = c[2] + c[3] + a[4] = a[1] + ... + a[4]
c[5] = a[5]
c[6] = c[5] + a[6] = a[5] + a[6]
c[7] = a[7]
c[8] = c[4] + c[6] + c[7] + a[8] = a[1] + ... + a[8]
c[9] = a[9]
c[10] = c[9] + a[10] = a[9] + a[10]
c[11] = a[11]
c[12] = c[10] + c[11] + a[12] = a[9] + ... + a[12]
c[13] = a[13]
c[14] = c[13] + a[14] = a[13] + a[14]
c[15] = a[15]
c[16] = c[8] + c[12] + c[14] + c[15] + a[16] = a[1] + ... + a[16]
......

4. 核心公式

c[x] = a[x-2^k] + ... + a[x] = a[x-lowbit(x)] + ... + a[x]
x的二进制表示最后k个0
lowbit(x) = x & -x , 表示一个数的二进制最低位的1在从右往左数的位置

5. 可解决的问题：

• ① 给某个位置上的数加上一个数**（单点修改）** O(log n)

  • 给某个位置上的数加一个数的代码：使a[x] + v

  for(int i = x;i <= n;i += lowbit(i))
  	c[i] += v;
  

• ② 求某一个前缀和**（区间查询）** O(log n)

  • c[x] + c[x-lowbit(x)] + ...
  • 求和代码(递归)

  int res = 0;
  for(int i = x;i > 0;i -= lowbit(i))
  	res += c[i];
  return res;
  

6.模板题

AcWing 1264. 动态求连续区间和

7.树状数组的三个核心函数

int lowbit(int x)
{
    return x & -x;
}

void add(int x,int v)
{
    for(int i = x;i <= n;i += lowbit(i))
        c[i] += v;
}

int query(int x)
{
    int res = 0;
    
    for(int i = x; i ;i -= lowbit(i))
        res += c[i];
    
    return res;
}

8.例题

AcWing 1265. 数星星
AcWing 1270. 数列区间最大值

---