一、对称矩阵
对n阶方阵,对任意a[i][j] == a[j][i] (1 <= i, j <= n),称其为对称矩阵
元素划分为三部分: 上三角区、主对角线、下三角区
元素a[i][j]在一维数组中存储对应下标K的关系如下(数组下标从0开始):
1.当 i >= j (下三角区、主对角线)
k = i(i - 1)/2 + j -1
2.当 i < j (上三角区)
k = j(j - 1)/2 + i - 1
二、三角矩阵
上三角区中元素为同一常量,元素下标对应关系:
1. 当i >= j (下三角区和主对角线)
k = i(i - 1)/2 + j - 1
2. 当i < j (上三角区)
k = n(n + 1) / 2 常量项
三、三对角矩阵
当|i - j| > 1时, 对任一元素a[i][j] == 0(1 < =i , j <= n),所有非零元素集中在主对角线为中心的三条对角线区域中,其他元素都为0
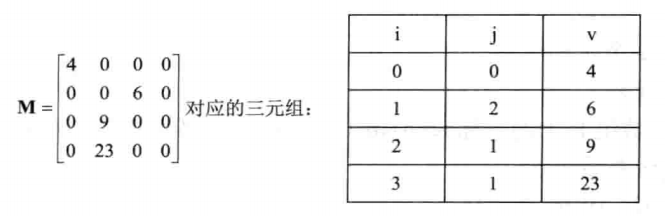
四、稀疏矩阵
矩阵中元素个数s相对于矩阵中非0元素个数t, s远远大于t时为稀疏矩阵
将其相应的行标、列标、值构成一个三元组,然后按照某种规律存储这些三元组,


























 2077
2077

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










