吴恩达深度学习笔记(37)-神经网络的权重初始化再解析

神经网络的权重初始化（Weight Initialization for Deep NetworksVanishing / Exploding gradients）

上节课，我们学习了深度神经网络如何产生梯度消失和梯度爆炸问题，最终针对该问题，我们想出了一个不完整的解决方案，虽然不能彻底解决问题，却很有用，有助于我们为神经网络更谨慎地选择随机初始化参数，为了更好地理解它，我们先举一个神经单元初始化地例子，然后再演变到整个深度网络。

我们来看看只有一个神经元的情况，然后才是深度网络。

单个神经元可能有4个输入特征，从x_1到x_4，经过a=g(z)处理，最终得到^{y，稍后讲深度网络时，这些输入表示为a}([l])，暂时我们用x表示。

z=w_1 x_1+w_2 x_2+⋯+w_n x_n，b=0，暂时忽略b，

为了预防z值过大或过小，你可以看到n越大，你希望w_i越小，因为z是w_i x_i的和，如果你把很多此类项相加，希望每项值更小，最合理的方法就是设置w_i=1/n，n表示神经元的输入特征数量，实际上，你要做的就是设置某层权重矩阵

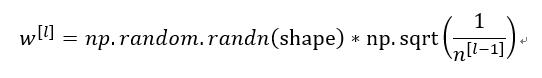
，n^([l-1])就是我喂给第l层神经单元的数量（即第l-1层神经元数量）。