深度学习入门

深度学习

深度学习一、基础1、基础概念什么是机器学习？2、机器学习算法分类（1）、有监督学习处理的问题：（2）、无监督学习处理的问题：（3）、强化学习3、数学知识二、神经网络1、全连接神经网络（MLP）（FC）感知器模型：2、神经元的原理3、sigmoid激活函数4、神经网络结构5、正向传播算法6、如何用于实际问题7、手写数字图像识别8、反向传播算法三、人工神经网络深入1、实验2、理论层面解释3、细节问题（1）、输入和输出值的设定：预测值一定要设置成one-hot编码形式（2）、网络的规模：根据你的规模和训练样本数进行选择，倘若样本数相对于网络的深度较少，会导致过拟合问题试！（3）、激活函数：（4）、损失函数的选择（5）、权重的初始化（6）、正则化（7）、学习率的设定（8）、动量项梯度下降法4、改进措施5、实际应用手写体识别，MNIST数据集的实现

非常好的老师！

整整150集！计算机博士竟然用视频的方式把《深度学习入门》讲解的如此通俗易懂！草履虫都学的会！（机器学习/计算机视觉/神经网络）_哔哩哔哩_bilibili

一、基础

1、基础概念

什么是机器学习？

从样本数据中学习，得到经验/模型，然后进行预测，是一种数据驱动的方法，与我们平常打比赛使用到的”算法“有所不同，机器学习中的算法是使用样本去预测数据

样本-机器学习算法处理的数据

特征向量-人工构造的用于描述一个样本的向量，如颜色、形状（n维），对于识别非常有用

预测函数-从样本的特征向量到预测值的映射

目标函数-训练时使用，目的是确定模型的参数

2、机器学习算法分类

（1）、有监督学习

监督信号-人工为样本打上的标签

事先用带有标签的样本进行训练，得到模型进行预测

什么样的东西是水果，什么样的东西是香蕉，人为打上标签

本质：根据样本学习得到一个映射函数

处理的问题：

分类问题（人脸识别、字符识别、语音识别，类别标签是整数编号

回归问题（确定一个实数值，如根据一个人的学历、行业、工作年限预测收入）

（2）、无监督学习

直接对数据进行预测，不带有人工标注的标签值

什么样的东西是水果，什么样的东西是香蕉，你自己看去

处理的问题：

聚类问题：将一批样本分成多个类，类别没有事先定义，而是由算法决定

数据降维问题：将一个向量变到低维空间

（3）、强化学习

根据当前的状态确定要执行的动作，以达到目标吗，下棋、自动驾驶，最大化回报，撞车扣一百，也可以quantify

3、数学知识

导数：在机器学习和深度学习中应用是求解目标函数的极值

目前想不到泰勒展开在这儿有什么用

向量：编程中体现为一维数组

向量的范数：将向量映射成一个非负的数

矩阵（学艺不精）：

特征值和特征向量：我们先来看它的定义，定义本身很简单，假设我们有一个n阶的矩阵A以及一个实数λ，使得我们可以找到一个非零向量x，满足：

Ax=λx

如果能够找到的话，我们就称λ是矩阵A的特征值，非零向量x是矩阵A的特征向量。

二次型：

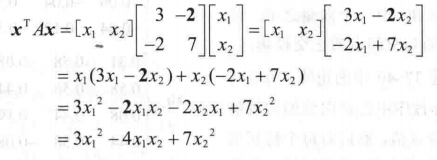
张量：向量是一阶张量，矩阵是二阶张量，RGB彩色图像是三阶张量（aijk），卷积神经网络一般输入的就是一个三阶张量

梯度：多元函数对各个自变量的一阶偏导数构成的向量

雅克比函数：

Hessian矩阵：

多元函数极值判别方法：类比一元函数，梯度相当于多元函数的一阶导，Hessian矩阵相当于多元函数的二阶导

多元函数泰勒展开

向量与矩阵求导：类比一元函数

条件概率与贝叶斯公式：

a发生的条件下b发生的概率

贝叶斯：推导出来的事件A\B若有因果关系则有先验概率和后验概率

随机变量：离散型（掷色子）连续型（无限不可列）概率密度函数（PDF）分布函数

二、神经网络

1、全连接神经网络（MLP）（FC）

受动物神经系统的启发

感知器模型：

2、神经元的原理

加权、激活

每一根传入神经对于该神经的影响程度不同，通过影响程度大小会有权重w

3、sigmoid激活函数

对输入数据进行变换（注：激活函数有很多，这里先介绍sigmoid函数）

4、神经网络结构

分层结构，先加权再激活形成输出信号

从l-1层到 l 层的映射就是神经网络的基本变换

5、正向传播算法

本质：多层复合函数

Tip：权重和偏置项通过训练得到，我理解的是刚开始权重和偏置项是不知道的，当输入大量样本和输出标签后，会自行得出每一个权重和偏置项的值，从而自己得出一个正确的多层复合函数

6、如何用于实际问题

输入层的神经元个数就是数据的维数

对于分类问题，分类结果为输出层神经元的最大值

对于回归问题，直接是输出层的值

7、手写数字图像识别

示例解析：现在有一个28*28像素的图片，初始有784个神经元，通过两次隐含层映射，输出层的神经元其他都是0.2，4号是0.8，既和四号相似度最高，则输入的图片就是4号

示例解析：我给定了一个m*n个像素的彩色的图片，现在需要捕捉人物面部信息（假设一共需要27个坐标），首先确定输入神经元，由于有m * n个像素，且是彩色像素，是由RGB形式（Red，Green，Blue三种颜色的比例），所以一共有3 * m * n个输入神经元，通过中间层，获得了27个坐标 ， 则一共有27 * 2 个输出神经元

8、反向传播算法

如何得到w 和 b？ 反向传播算法加梯度下降法让损失函数最小化，使得训练样本和输入样本得到的值差值尽可能 小得到 ，之前我猜的是人工输入数据，不知道对不对

（xi，yi）分别为输入值和标签值，h（xi）是通过输入值得到的输出值

L（W） 为损失函数

推导：听不懂

求导的整体思路：

正式推导：

η为学习率

三、人工神经网络深入

1、实验

网络层数与各层神经元数量

设置激活函数和参数

设置训练参数、包括最大迭代次数、迭代终止阈值、学习率、动量项系数

生成训练样本，设置样本标签值

调用训练函数

2、理论层面解释

神经网络的拟合能力：万能逼近定理指出，只要有隐含层，激活函数选取得当，神经元个数足够，拟合出来的就是真实的函数，想要多接近就有多接近，但是需要注意过拟合问题

3、细节问题

（1）、输入和输出值的设定：预测值一定要设置成one-hot编码形式

比如识别时我需要输出0-9的整数，不直接输入“9” 而是变为一个向量，（0，0，0，0，0，0，0，0，1）表示 9，类别类变量、多分类问题的类标签最好都设置成这种形式

归一化：将256变为256/257

（2）、网络的规模：根据你的规模和训练样本数进行选择，倘若样本数相对于网络的深度较少，会导致过拟合问题

各层神经元的数量而言，输入层和输出层是确定的，隐含层根据经验而定，设置为2^n个，以提高计算和存储效率，具体情况具体分析，需要去

试！

（3）、激活函数：

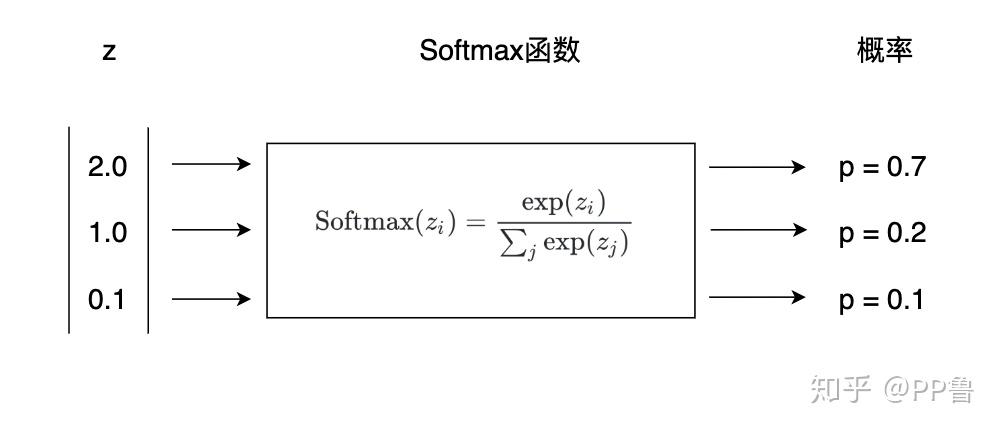
对于多分类问题，一种常用的方法是Softmax函数，它可以预测每个类别的概率。对于阿拉伯数字预测问题，选择预测值最高的类别作为结果即可。Softmax的公式如下，其中z是一个向量，zi和zj是其中的一个元素。

Softmax(zi)=exp⁡(zi)∑jexp⁡(zj)

下图中，我们看到，Softmax将一个[2.0,1.0,0.1]的向量转化为了[0.7,0.2,0.1]，而且各项之和为1。

为什么需要激活函数？

我们来check一个问题，以图中的多层函数h（x）为例，通过两个隐含层和一个输出层，里面每一层的输入值都是一个线性量，想象一下，如果将激活函数去掉会发生什么？这个函数不论经过多么深多么复杂的拟合，得到的都是一个线性函数！也就是说，我不加入激活函数得到的目标函数是一个点集，当我输入新的样本时，只有之前输入过的相同样本才会在函数中得到映射，但当我加入了激活函数，那么非样本量就可以得到预测，这也是人工神经网络的底层原理中最核心的一个词语，所以，可以说，这个激活函数就是全连接人工神经网络的核心

如何选择？单调递增，连续，几乎处处可到，导数不为零（会导致饱和性-梯度消失问题）

（4）、损失函数的选择

回归问题：欧式距离

分类问题：交叉熵

p（x）为真实概率（一个是1，其他是0），q（x）为拟合概率（加起来和为1）

（5）、权重的初始化

用随机数进行初始化，均匀分布，正态分布

（6）、正则化

（7）、学习率的设定

为什么要设置学习率？

（8）、动量项梯度下降法

加快收敛速度减小震荡

4、改进措施

梯度消失（爆炸）问题，ReLU一定程度上缓解该问题

激活函数的饱和性：激活函数的导数等于零

局部极小值：有陷入局部极小值的风险，会收敛到一个出乎意料的值

鞍点问题：Hessian矩阵不定，不是局部极值点

人工神经网络拟合出来的函数如下：

5、实际应用

人脸检测、人脸识别、光学字符识别、手写字符识别、自然语言处理

手写体识别，MNIST数据集的实现

import torch
from torch.utils.data import DataLoader
from torchvision import transforms
from torchvision.datasets import MNIST
import matplotlib.pyplot as plt
​
​
class Net(torch.nn.Module):
​
    def __init__(self):
        super().__init__()
        self.fc1 = torch.nn.Linear(28*28, 64)
        self.fc2 = torch.nn.Linear(64, 64)
        self.fc3 = torch.nn.Linear(64, 64)
        self.fc4 = torch.nn.Linear(64, 10)
    
    def forward(self, x):
        x = torch.nn.functional.relu(self.fc1(x))
        x = torch.nn.functional.relu(self.fc2(x))
        x = torch.nn.functional.relu(self.fc3(x))
        x = torch.nn.functional.log_softmax(self.fc4(x), dim=1)
        return x
​
​
def get_data_loader(is_train):
    to_tensor = transforms.Compose([transforms.ToTensor()])
    data_set = MNIST("", is_train, transform=to_tensor, download=True)
    return DataLoader(data_set, batch_size=15, shuffle=True)
​
​
def evaluate(test_data, net):
    n_correct = 0
    n_total = 0
    with torch.no_grad():
        for (x, y) in test_data:
            outputs = net.forward(x.view(-1, 28*28))
            for i, output in enumerate(outputs):
                if torch.argmax(output) == y[i]:
                    n_correct += 1
                n_total += 1
    return n_correct / n_total
​
​
def main():
​
    train_data = get_data_loader(is_train=True)
    test_data = get_data_loader(is_train=False)
    net = Net()
    
    print("initial accuracy:", evaluate(test_data, net))
    optimizer = torch.optim.Adam(net.parameters(), lr=0.001)
    for epoch in range(2):
        for (x, y) in train_data:
            net.zero_grad()
            output = net.forward(x.view(-1, 28*28))
            loss = torch.nn.functional.nll_loss(output, y)
            loss.backward()
            optimizer.step()
        print("epoch", epoch, "accuracy:", evaluate(test_data, net))
​
    for (n, (x, _)) in enumerate(test_data):
        if n > 3:
            break
        predict = torch.argmax(net.forward(x[0].view(-1, 28*28)))
        plt.figure(n)
        plt.imshow(x[0].view(28, 28))
        plt.title("prediction: " + str(int(predict)))
    plt.show()
​
​
if __name__ == "__main__":
    main()
​