文章介绍了PCA（主成分分析）的概念、基本原理，列举了其在数据压缩、特征提取、预处理和图像处理中的应用，以及如何通过Python（如Scikit-learn）进行数据降维的代码示例。强调了PCA作为数据处理关键技术的重要性和注意事项。
一、PCA的概念及应用领域
PCA（Principal Component Analysis，主成分分析）是一种常用的多变量数据分析方法，用于降低数据维度、提取关键特征以及数据可视化等领域。
PCA的基本概念是找到数据中最相关的方向，将原始高维数据转换为新的低维坐标系，使得数据在新的坐标系下具有最大的方差。通过线性变换，PCA可以将原始数据集投影到一组正交的主成分上，其中第一个主成分解释了数据中最大的方差，第二个主成分解释了第二大的方差，依此类推。
PCA在许多领域都有广泛的应用，包括但不限于：
-
数据压缩与降维：PCA可以将高维数据转化为低维表示，减少数据的存储空间和计算成本，同时保留数据中的主要信息。
-
特征提取与选择：通过PCA，可以从高维数据中提取出最具代表性的特征，帮助解决特征维度过高导致的维数灾难问题。
-
数据预处理：PCA可以用于去除数据中的冗余性和噪声，提高后续数据分析和建模的效果。
-
图像处理：PCA在图像处理中被广泛应用，如人脸识别、图像压缩、图像去噪等。
-
数据可视化：通过PCA将高维数据降至二维或三维空间，可以实现数据的可视化展示，帮助分析和理解数据。
总之，PCA是一种强大而灵活的数据分析工具，在多个领域中都发挥着重要作用，帮助提取数据的关键信息、简化数据分析过程并改善数据可视化效果。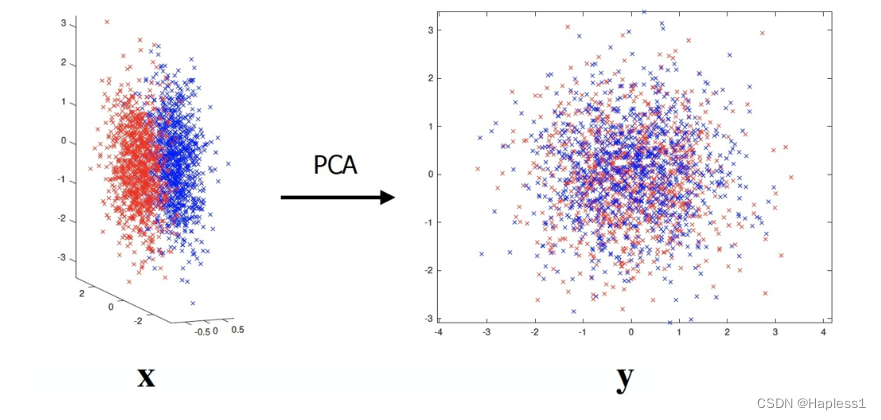
二、PCA的基本原理
假设有m个样本和n个特征的数据集X，可以先对数据进行预处理，去除均值，并将每个特征缩放为单位方差。然后，计算数据集X的协方差矩阵C，其中第(i,j)个元素表示第i个特征和第j个特征之间的协方差，即：
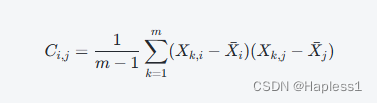
其中，
表示第i个特征的均值。
接下来，对协方差矩阵进行特征值分解，得到一组正交的特征向量和特征值。特征向量表示数据变换后的主成分方向，特征值表示在每个主成分方向上的方差。根据特征值大小，选择前k个主成分，将原始数据集投影到这些主成分上，得到新的低维数据表示。
具体地，如果对协方差矩阵进行特征值分解，得到特征向量V={v1,v2,...,vn}和特征值λ={λ1,λ2,...,λn}，则前k个主成分可以表示为矩阵Wk=[v1,v2,...,vk]，新的低维数据表示为Y=XWk。其中，每一行表示一个样本的新的低维表示，每列表示一个主成分。
通过PCA降维，可以减少数据的存储空间和计算成本，同时保留数据中的主要信息。同时，PCA也可以用于特征提取和选择，从而帮助解决高维数据的问题。
三、PCA算法步骤
-
数据预处理：对原始数据进行预处理操作，例如去除均值、缩放特征等，以确保数据符合PCA的要求。
（1）.标准化（Standardization）：通过减去特征的均值并除以标准差，将特征缩放为零均值和单位方差。这样做可以保持数据的形状不变，并且可以消除不同特征尺度的差异。
（1）.去除均值（Mean Removal）：对数据进行均值去除是为了消除数据中的偏置或平移，使得数据的中心位于原点。去除均值可以保持数据的形状不变，只是将数据的中心移到原点，这样可以避免主成分受到数据中心的影响。
（2）.缩放特征（Feature Scaling）：在PCA中，不同的特征可能具有不同的尺度和单位，这可能导致某些特征在计算协方差矩阵时具有更大的影响力。为了消除这种影响，常常需要对特征进行缩放，使得它们具有相似的尺度。常见的缩放方法包括标准化（Standardization）和归一化（Normalization）。
（2）.归一化（Normalization）：将特征缩放到一定范围内，常见的归一化方法包括将特征缩放到[0,1]或[-1,1]范围内。归一化可以保持数据的形状不变，并且可以将特征值限制在一定的范围内。
-
去除异常值（Outlier Removal）：异常值可能对PCA的结果产生较大的影响，因为PCA是一种基于方差的方法，异常值的存在可能导致方差过大，从而影响主成分的计算。因此，在进行PCA之前，建议去除异常值，以保证结果的准确性。
-
计算协方差矩阵：对预处理后的数据计算协方差矩阵。协方差矩阵是一个对称矩阵，其中第(i,j)个元素表示第i个特征和第j个特征之间的协方差。协方差矩阵的计算可以使用以下公式：
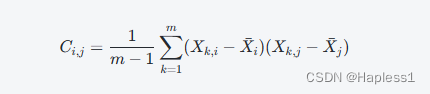
其中，m表示样本数量，Xk,i表示第k个样本的第i个特征，
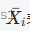表示第i个特征的均值。 -
特征值分解：对协方差矩阵进行特征值分解，得到一组正交的特征向量和特征值。特征向量表示数据变换后的主成分方向，特征值表示在每个主成分方向上的方差。特征值分解可使用常见的数值计算方法，例如奇异值分解（Singular Value Decomposition，SVD）或特征值分解（Eigenvalue Decomposition）。
-
选择主成分：根据特征值的大小，选择前k个主成分。通常情况下，可以根据特征值的累计贡献率来确定保留的主成分数量。累计贡献率表示前k个主成分所解释的总方差占总方差的比例。
-
降维过程：将原始数据集投影到选定的主成分上，得到新的低维数据表示。具体地，选择前k个特征向量组成矩阵Wk=[v1,v2,...,vk]，其中vi表示第i个特征向量。然后，将原始数据集X与矩阵Wk进行矩阵乘法运算，得到新的低维数据表示Y=XWk。每一行表示一个样本的新的低维表示，每列表示一个主成分。
通过PCA降维，可以减少数据的存储空间和计算成本，同时保留数据中的主要信息。降维后的数据可以用于可视化、分类、聚类等任务，同时也有助于减少数据中的噪声和冗余信息，提高后续数据分析和建模方法的效果。
四、代码示例
import numpy as np
import matplotlib.pyplot as plt
# 加载鸢尾花数据集
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data # 特征矩阵
y = iris.target # 标签
# 数据标准化
X_mean = np.mean(X, axis=0) # 每个特征的均值
X_std = np.std(X, axis=0) # 每个特征的标准差
X_normalized = (X - X_mean) / X_std
# 计算协方差矩阵
cov_matrix = np.cov(X_normalized.T)
# 计算特征值和特征向量
eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)
# 选择主成分数量
n_components = 2
eigenvectors_selected = eigenvectors[:, :n_components]
# 将数据投影到选定的主成分上
X_pca = X_normalized.dot(eigenvectors_selected)
# 绘制降维后的数据散点图
colors = ['navy', 'turquoise', 'darkorange']
target_names = iris.target_names
for color, i, target_name in zip(colors, [0, 1, 2], target_names):
plt.scatter(X_pca[y == i, 0], X_pca[y == i, 1], color=color, alpha=0.8, lw=2, label=target_name)
plt.legend(loc='best', shadow=False, scatterpoints=1)
plt.title('PCA of Iris dataset')
plt.show()
首先加载鸢尾花数据集并进行数据标准化，然后计算协方差矩阵。接下来，使用np.linalg.eig函数计算协方差矩阵的特征值和特征向量。然后，选择要保留的主成分数量，并将选定的特征向量用于将数据投影到选定的主成分上。最后，使用散点图将降维后的数据可视化展示。
接下来展示使用库函数简洁实现的方法：
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
# 加载鸢尾花数据集
iris = load_iris()
X = iris.data # 特征矩阵
y = iris.target # 标签
# 创建PCA对象并进行降维
n_components = 2 # 设置保留的主成分数量
pca = PCA(n_components=n_components)
X_pca = pca.fit_transform(X)
# 绘制降维后的数据散点图
colors = ['navy', 'turquoise', 'darkorange']
target_names = iris.target_names
for color, i, target_name in zip(colors, [0, 1, 2], target_names):
plt.scatter(X_pca[y == i, 0], X_pca[y == i, 1], color=color, alpha=0.8, lw=2, label=target_name)
plt.legend(loc='best', shadow=False, scatterpoints=1)
plt.title('PCA of Iris dataset')
plt.show()
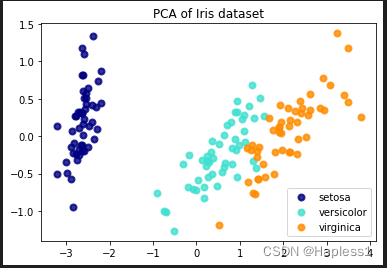
使用Scikit-learn库中的load_iris函数加载鸢尾花数据集，并将特征矩阵X和标签数组y分别赋值。然后，创建了一个PCA对象，并设置要保留的主成分数量为2，以便将数据降至二维。接下来，使用fit_transform方法对数据集进行降维操作，得到降维后的数据集X_pca。最后，使用散点图将降维后的数据可视化展示，并按照不同类别用不同颜色进行标记。
五、总结
PCA作为一种常用的降维和特征提取技术，在数据处理和模型构建中扮演着重要角色。通过降低数据维度和提取重要特征，PCA可以简化数据表示、提高计算效率和模型性能。然而，在应用PCA时需要注意其假设和局限性，并结合具体问题进行调优和扩展。
扫一扫
1058
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
