JZ6 旋转数组的最小数字

描述

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。
输入一个非递减排序的数组的一个旋转，输出旋转数组的最小元素。
NOTE：给出的所有元素都大于0，若数组大小为0，请返回0。

旋转数组是：

这道题也用二分查找法是我没注意的细节了，因为该数组旋转后可以发现由最小的那个元素把两个子数组分开了，左边的子数组的元素都大于或等于后面子数组的元素。

而我们要找的就是那个最小的元素。

两个子数组的元素都是递增数组。

讨论组题解：（没有重复数字的时候，如果有重复数字还是遍历数组）

①首先用两个指针left,right分别指向数组的第一个元素和最后一个元素。

 

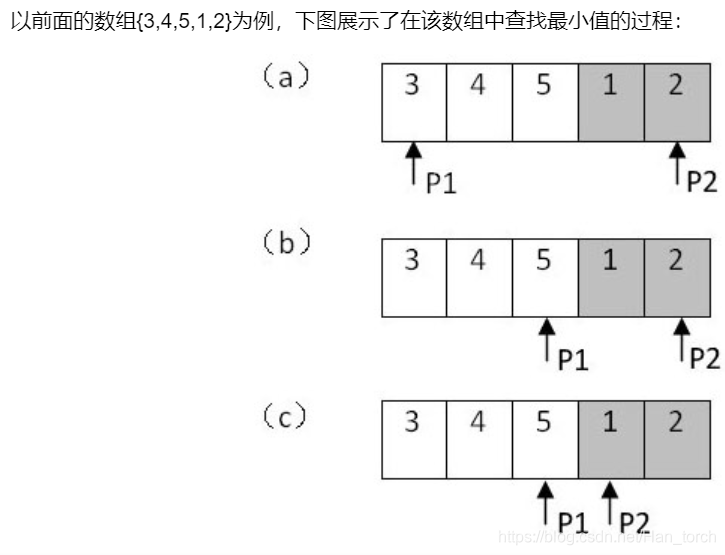
②然后找到目前数组的中间元素，第一种情况是中间元素比第一个元素大，则中间元素位于前面的子数组。

说明此时的最小的元素位于中间元素的后面，所以我们可以让第一个指针left指向中间元素。如上图(b)。第一个指针仍然位于前面的子数组中。

第二种情况是，中间元素小于第一个元素，则中间元素位于后面的子数组，此时最小元素位于中间元素的前面，可以让第二个指针right指向中间元素。第二个指针仍然位于后面的子数组中。

③

按照以上思路，第一个指针left总是指向前面递增数组的元素，第二个指针right总是指向后面递增的数组元素。

最终第一个指针将指向前面数组的最后一个元素，第二个指针指向后面数组中的第一个元素。

也就是说他们将指向两个相邻的元素，而第二个指针指向的刚好是最小的元素，这就是循环的结束条件。

因为是旋转数组，所以前面的子数组是比后面的子数组大的，所以第二个指针指向的后面子数组的第一个元素就是最小的元素。

#include <iostream>
#include <vector>
#include <string>
#include <stack>
#include <algorithm>
using namespace std;

class Solution {
public:
    int minNumberInRotateArray(vector<int> rotateArray) {
        int size = rotateArray.size();
        if(size == 0){
            return 0;
        }//if
        int left = 0,right = size - 1;
        int mid = 0;
        // rotateArray[left] >= rotateArray[right] 确保旋转
        while(rotateArray[left] >= rotateArray[right]){
            // 分界点
            if(right - left == 1){
                mid = right;
                break;
            }//if
            mid = left + (right - left) / 2;
            // rotateArray[left] rotateArray[right] rotateArray[mid]三者相等
            // 无法确定中间元素是属于前面还是后面的递增子数组
            // 只能顺序查找
            if(rotateArray[left] == rotateArray[right] && rotateArray[left] == rotateArray[mid]){
                return MinOrder(rotateArray,left,right);
            }//if
            // 中间元素位于前面的递增子数组
            // 此时最小元素位于中间元素的后面
            if(rotateArray[mid] >= rotateArray[left]){
                left = mid;
            }//if
            // 中间元素位于后面的递增子数组
            // 此时最小元素位于中间元素的前面
            else{
                right = mid;
            }//else
        }//while
        return rotateArray[mid];
    }
private:
    // 顺序寻找最小值
    int MinOrder(vector<int> &num,int left,int right){
        int result = num[left];
        for(int i = left + 1;i < right;++i){
            if(num[i] < result){
                result = num[i];
            }//if
        }//for
        return result;
    }
};

int main(){
    Solution s;
    //vector<int> num = {0,1,2,3,4,5};
    //vector<int> num = {4,5,6,7,1,2,3};
    vector<int> num = {2,2,2,2,1,2};
    int result = s.minNumberInRotateArray(num);
    // 输出
    cout<<result<<endl;
    return 0;
}