从自己挖的坑里爬出来

背景

公司的活儿需要做轨迹拟合，数据量不大，不想使用各种库啥的，毕业后似乎就没再用过高中数学，借此机会想着复习一下，过程中遇到小小问题却困扰了两周，在此记录一下。

过程

网上搜了线性拟合的文章看

这段儿似乎还好理解，虽然对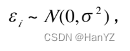 没的表示方式有点儿蒙，好在还不影响理解。紧接着，就被下段的 ∂ 当头一棒

搜索“偏导数符号”B站 www.bilibili.com/read/cv1068455 这篇文章讲解的不错，然后又断断续续的复习了导数、导函数、偏导数、偏导函数。还好现在不是写代码的主力，早已让年轻人开干，无需等自己彻底弄明白。
回过头再看原理，（式3）怎么都过不到（式4），郁闷之余寻友求助

看了又看，依旧困惑，直到今日，周六的办公楼，整层只有我一人，拿出纸笔

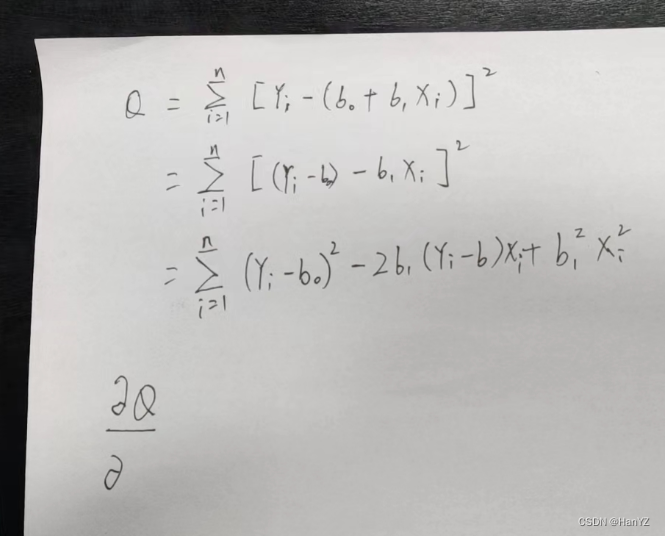
画到这儿，我终于意识到我困在自己挖的坑里了——原理里讲的是b0的偏导，我心里一直推导的是
Xi的偏导

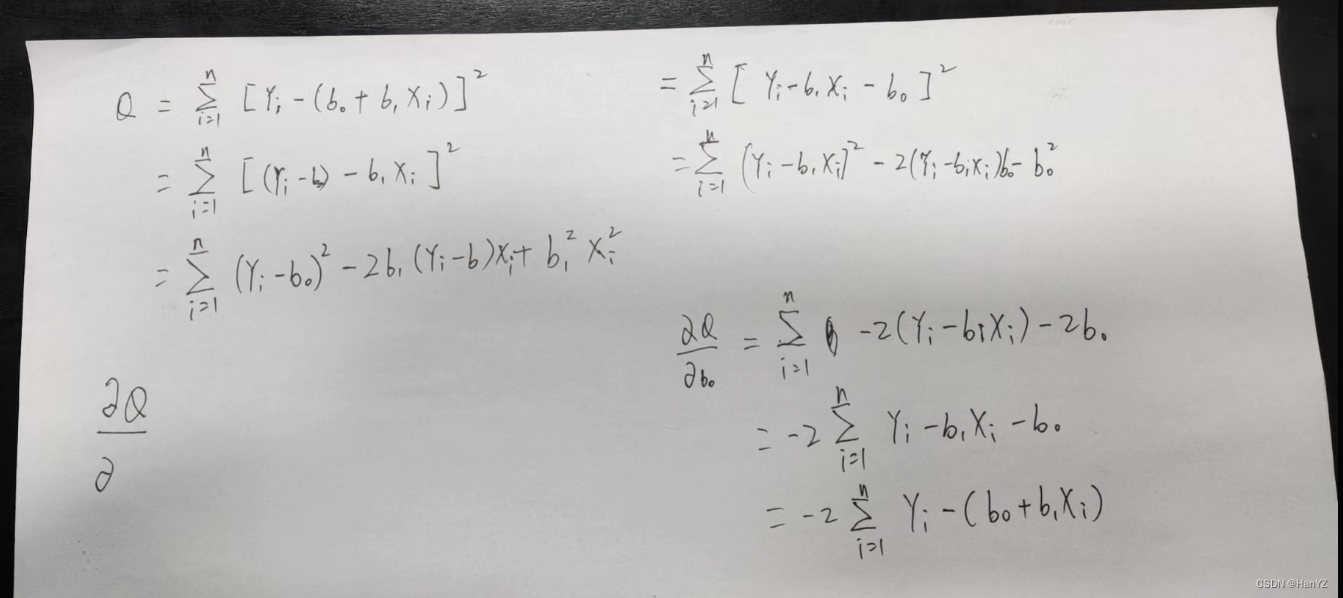
x——天生的自变量，几乎所有讲偏导的都首先对x求偏导，所以，第一次看到这儿，就跟着潜意识对X偏导，而后每次零碎的复习几眼再回来看，都一直在坑儿里。直到今天有了闲暇，静下心来动手去写。

总结

这种坑，不写出来，只去求助别人，别人可能也被问的很晕，只会觉得（式3）到（式4）不是显而易见么，要怎么指导你 😦
学习，还是要静下心来才好 😃