链式二叉堆

最新推荐文章于 2024-04-19 12:25:57 发布

原创最新推荐文章于 2024-04-19 12:25:57 发布 · 656 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#C #数据结构 #堆 #链表

数据结构专栏收录该内容

31 篇文章

订阅专栏

Notes

写堆一般用数组，数组的下标可方便地实现二叉树的逻辑，并且在写堆时保证其是棵完全二叉树，也就保证高度是 $O(log n)$ 的，维护的复杂度也是 $O(log n)$ 。
之前数组版的堆实现：heap。删除、插入的原理和实现参照此篇。
现尝试用链式结构实现二叉堆，保持跟数组实现一样的复杂度。
小顶堆为例（其实看你怎么重载小于号），数据类型就int吧。

Structure

原始想法
两个结构体：
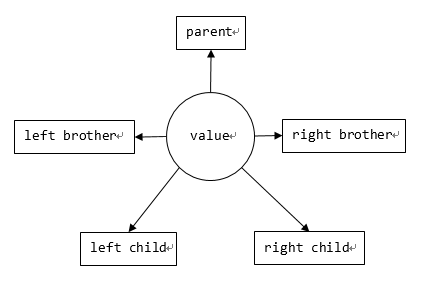
结点的结构，像写二叉树一样，两个指针指子结点。但添加元素时要自下而上调整，故加一个指向父结点的指针。

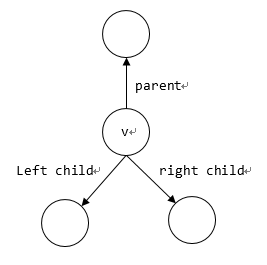
堆的结构，就维护一个树根指针root。
考虑树高
想有数组版的复杂度，想到让树的形态也能是完全二叉树，控制树高在 $O(log n)$ ，那么添加和删除物理结点都在于最后一个元素，于是堆结构多维护一个last指针指向最后一个元素。
考虑删除
数组版删除时，先将最后一个元素的值覆盖堆顶，再自顶向下调整元素，以维护堆的性质。
对链版，将last所指覆盖到堆顶后，要free掉原来的last，并让它指向前一个元素。
为了快速完成更新，考虑结点加一个指针lb（Left Brother）指向它的前一个结点。在插入新结点时，就可让新结点的 Left Brother 指向旧的last，然后再更新last。

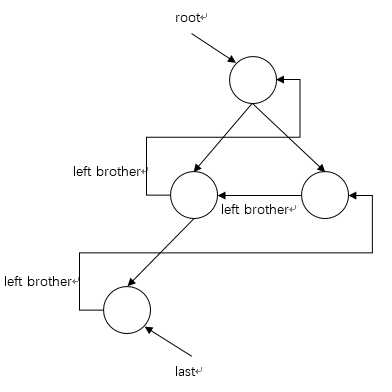
Left Brother 指针实际上就通过前驱关系把结点串成一维结构，实现类似数组的线性逻辑。
考虑插入
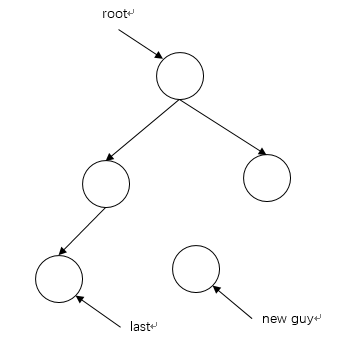
插入时，要将新建的结点放在last之后，先不考虑边界（树根附近），有两种情况：
当last所指是左儿子（即*last是左儿子），只要找到*last的父节点，将新结点作为它右儿子，然后更新last；

当last所指是右儿子，找到*last的父结点 F 后，还要找到 F 的后面一个结点 F’，然后将新结点插为 F’ 的左儿子，然后更新last；

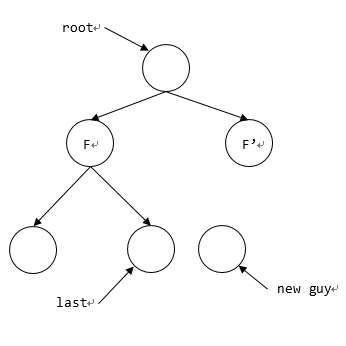
后一个结点也可能在下一层：

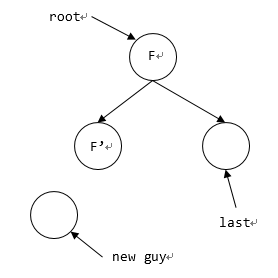
为快速找到 F’，考虑结点加个指针rb（Right Brother），指向结点的后一个结点。其维护类似于 Left Brother，也在插入新结点时完成。

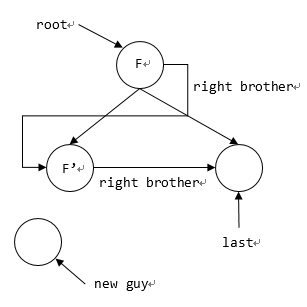
Right Brother 与 Left Brother 类似，实现的是后继。
最终…

~~这是个什么东西噢…老老实实用数组写好不啦~~

Code

~~“Talk is cheap. Show me the code.”~~
~~“来你的哇”~~

heap.h

/* heap.h */
#ifndef _HEAP_H
#define _HEAP_H

#ifndef DataType
#define DataType int

/* 堆结点 */

typedef struct h_node
{
    DataType v;       // value
    struct h_node *p, // parent
            *lc, *rc, // left child, right child
            *lb, *rb; // left brother, right brother
} Hnode;

/* 堆 */

typedef struct
{
    Hnode *root, // 根
          *last; // 最后一个元素
    // 重载小于号
    // if 左 < 右 : 返回真
    // else : 返回假
    int (*less)(const void *, const void *);
} Heap;

/* 判空 */
int empty (Heap);
/* 插入 */
Hnode* insert (Heap*, DataType value);
/* 新堆，传小于号进来 */
Heap heap (int (*less)(const void *, const void *));
/* 弹顶 */
void pop (Heap*);
/* 堆顶 */
int top (Heap);

#endif // DataType
#endif // _HEAP_H

heap.c

/* heap.c */
#include <stdlib.h>
#include "heap.h"

/* 初始化过的新结点 */
static Hnode* _heap_node()
{
    Hnode *n = (Hnode*)malloc(sizeof(Hnode));
    if (n)
        n->p = n->lc = n->rc = n->lb = n->rb = NULL;
    return n;
}

/* 交换 */
static void _swap(DataType *a, DataType *b)
{
    DataType c = *a;
    *a = *b;
    *b = c;
}

/* 新堆 */
Heap heap(int (*f)(const void *, const void *))
{
    Heap h;
    h.root = h.last = NULL;
    h.less = f;
    return h;
}

/* 判空 */
int empty(Heap h)
{
    return !h.root;
}

/* 堆顶 */
int top(Heap h)
{
    return h.root->v;
}

/* 弹堆顶 */
void pop(Heap *h)
{
    if (!h || empty(*h))
        return;

    Hnode *q;

    // 只有一个元素
    if (h->root == h->last)
    {
        free(h->root);
        h->root = h->last = NULL;
        return;
    }

    h->root->v = h->last->v; // cover the top

    // 父子关系
    q = h->last->p; // parent
    if (q->lc == h->last) // is left child
        q->lc = NULL;
    else // is right child
        q->rc = NULL;

    // 兄弟关系
    q = h->last->lb; // its left brother
    q->rb = NULL;

    free(h->last);

    // 更新 last 指针
    h->last = q;

    // 维护堆性质
    q = h->root;
    for (Hnode *ch; ; q = ch)
    {
        // find smaller child
        ch = q->lc;
        if (!ch) break;
        // right < left
        if (q->rc && h->less(&q->rc->v, &ch->v))
            ch = q->rc;

        // parent < child
        if (h->less(&q->v, &ch->v))
            break;

        _swap(&q->v, &ch->v);
    }
}


/* 插入 */
Hnode* insert(Heap *h, int v)
{
    if (!h) return NULL;

    Hnode *new_guy = _heap_node(), *your_father;

    if (!new_guy) return NULL;

    new_guy->v = v;

    // 空堆
    if (empty(*h))
    {
        h->root = h->last = new_guy;
        return new_guy;
    }

    // 单结点
    if (h->root == h->last)
    {
        h->root->lc = h->root->rb = new_guy;
        new_guy->p = new_guy->lb = h->root;
        h->last = new_guy;

        // adjustment
        if (h->less(&v, &h->root->v))
        {
            new_guy->v = h->root->v;
            h->root->v = v;
        }

        return new_guy;
    }

    // 多结点

    // 兄弟关系
    new_guy->lb = h->last;
    h->last->rb = new_guy;

    // 父子关系
    your_father = h->last->p;
    if (your_father->lc == h->last) // is left child
    {
        your_father->rc = new_guy;
        new_guy->p = your_father;
    }
    else // is right child
    {
        // your father changes to
        // your father's right brother
        your_father = your_father->rb;
        your_father->lc = new_guy;
        new_guy->p = your_father;
    }

    // 更新 last 指针
    h->last = new_guy;

    // 维护堆性质
    for (Hnode *now = new_guy, *fa; ; now = fa)
    {
        fa = now->p;
        // no father || father < child
        if (!fa || h->less(&fa->v, &now->v))
            break;

        _swap(&fa->v, &now->v);
    }

    return new_guy;
}

Testing

~~"I don't believe in you."~~

main.c

#include <stdio.h>
#include "heap.h"

int cmp(const void *a, const void *b)
{
    return *(int*)a < *(int*)b;
}

int main()
{
    Heap h = heap(cmp);
    insert(&h, 3);
    insert(&h, -1);
    insert(&h, 10);
    insert(&h, 5);
    insert(&h, 100);
    insert(&h, -345435);
    insert(&h, 0);
    while (!empty(h))
    {
        printf("%d\n", top(h));
        pop(&h);
    }
    return 0;
}