位运算之二进制中1的个数

位运算是把数字用二进制表示之后，对每一位上0或1的运算。

位运算有五种运算：与、或、异或、左移、右移。

• 与、或、异或的运算规律
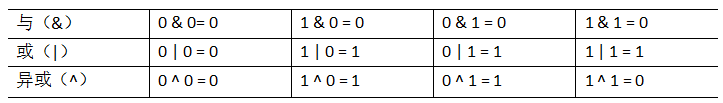
• 左移（<<）     m << n 表示把 m 左移 n 位。在左移 n 位的时候，最左边的 n 位将被丢弃，同时在最右边补上 n 个0。

例如：10001010 << 3 = 01010000

• 右移（>>）     m >> n 表示把 m 右移 n 位。在右移 n 位的时候，最右边的 n 位将被丢弃，但右移时处理最左边位的情形要复杂一些：

如果数字是一个无符号数值，则用0填补最左边的 n 位；

如果数字是一个有符号数值，则用数字的符号位填补最左边的 n 位。

例如：00001011 >> 2 = 00000010

           10001010 >>2 = 11100010

例题：二进制中1的个数

题目：请实现一个函数，输入一个整数，输出该数二进制表示中1的个数。例如把9表示成二进制是1001，有2位是1。因此如果输入9，该函数输出2。

常规解法：先判断该整数二进制表示中最右边位是不是1，接着把输入的整数右移一位，此时原来处于从右边数起的第二位被移到最右边了，再继续判断最右边位是不是1；这样每次移动一位，直到整个整数变成0为止。

int NumberOF1(int n)
{
    int count = 0;
    while( n )
    {
        if(n & 1)
        {
            count++;
        }       
        n = n >> 1; //原来处于从右边数起的第二位被移到最右边
    }
    return count;
}

但是这样的算法可能会引起死循环，当该整数为负数时，并不是简单的将最高位的1移到第二位，而是仍要保证移位后是一个负数，即移位后的数最高位还是1。

优秀解法：把一个整数减去1，再和原整数做与运算，会把该整数最右边的1变成0；那么一个整数的二进制中有多少个1，就可以进行多少次这样的操作。

int NumberOF1(int n)
{
    int count = 0;
    while( n )
    {
        count++;
        n = n & (n-1); //把n的二进制表示里最右边的1变为0
    }
    return count;
}