leetcode刷题记录：[764]最大加号标志-优快云博客

本文链接：https://blog.youkuaiyun.com/HSJSJH/article/details/134421654

文章描述了一种在给定的二维矩阵中找到最大阶数的轴对齐加号标志的问题，通过动态规划方法计算每个点及其周围4个方向的阶数，最后返回所有点中最小的阶数。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目：

在一个 n x n 的矩阵 grid 中，除了在数组 mines 中给出的元素为 0，其他每个元素都为 1。mines[i] = [xi, yi]表示 grid[xi][yi] == 0

返回 grid 中包含 1 的最大的 轴对齐 加号标志的阶数 。如果未找到加号标志，则返回 0 。

一个 k 阶由 1 组成的 “轴对称”加号标志 具有中心网格 grid[r][c] == 1 ，以及4个从中心向上、向下、向左、向右延伸，长度为 k-1，由 1 组成的臂。注意，只有加号标志的所有网格要求为 1 ，别的网格可能为 0 也可能为 1 。

示例 1：

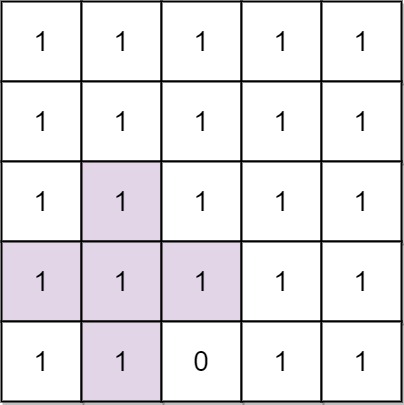
输入: n = 5, mines = [[4, 2]]
输出: 2
解释: 在上面的网格中，最大加号标志的阶只能是2。一个标志已在图中标出。

示例 2：

输入: n = 1, mines = [[0, 0]]
输出: 0
解释: 没有加号标志，返回 0 。

提示：

1 <= n <= 500
1 <= mines.length <= 5000
0 <= xi, yi < n
每一对 (xi, yi) 都 不重复

Related Topics

数组
动态规划

思路：

定义一个三维数组，前两个值分别代表其点的横纵坐标，第三个值代表其值。然后分别计算各点各方向的阶。采用动态规划的思想。

代码：

class Solution {
    public int orderOfLargestPlusSign(int n, int[][] mines) {
        // 初始化4个方向的阶
        int [][][] dp = new int[n][n][4];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                for (int k = 0; k < 4; k++) dp[i][j][k] = 1;
            }
        }
        for (int[] z : mines) {
            for (int k = 0; k < 4; k++) {
                dp[z[0]][z[1]][k] = 0;
            }
        }
        // 算左和上方向的阶
        for (int i = 1; i < n; i++) {
            for (int j = 1; j < n; j++) {
                if (dp[i][j][0] == 0){
                    continue;
                }
                dp[i][j][0] = 1 + dp[i][j-1][0];
                dp[i][j][1] = 1 + dp[i-1][j][1];
            }
        }

         // 算右和下方向的阶
        for (int i = n-2; i >= 0; i--) {
            for (int j = n-2; j >= 0 ; j--) {
                if (dp[i][j][2] == 0){
                    continue;
                }
                dp[i][j][2] = 1 + dp[i][j+1][2];
                dp[i][j][3] = 1 + dp[i+1][j][3];
            }
        }

        // 遍历各点各方向的值
        int res = 0;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                int k = Math.min(Math.min(dp[i][j][0], dp[i][j][1]), Math.min(dp[i][j][2],  dp[i][j][3]));
                res = Math.max(res,k);
            }
        }
        return res;
    }
}