【论文笔记】Top-K Possible Shortest Path Query

本文的主要贡献在于给出了不确定图中一条路径是最短路径的概率的上下限，并在此基础上提出了一个过滤-细化框架来回答kSP查询。我们通过大量的实验证明了我们方法的优越性。

1. Introduction
   
   
   
   
   
   
   
   
   
   存在。注意，在不确定图G中，E(Pi)和E(Pn)都不是原子事件，因为路径Pi(Pn)是由几条边组成的。因此，路径Pi 1和Pi2(1 ≤ i1，i2≤n-1)可能有公共边。在这种情况下，我们必须使用包含-排除原理来评估等式1。这就是kSP查询和top-k查询在不确定关系表上的关键区别[8]。众所周知，包含-排除原理具有指数时间复杂度，因此，用包含-排除原理来回答kSP查询是相当昂贵的。更多细节将在第2节讨论。
   为了提高查询性能，我们采用了过滤和细化框架。本文的主要贡献是定义了具有线性计算复杂度的适当界。然后，基于该界限，我们可以为kSP查询找到候选路径，而无需任何排除。在细化过程中，对于每个候选路径，我们利用蒙特卡罗模拟来估计路径。最后，向用户报告前k条可能的最短路径。
   1 .在经典的确定性图上的top-k最短路径算法的基础上，我们提出了一个过滤-细化框架来回答大型不确定图中的top-k最短路径查询。
   2.我们设计了两个不同的下界来估计一条路径P是不确定图G上的最短路径的概率，其中，第一个基于路径独立性假设，第二个基于近似的基于“集合覆盖”的方法(它具有线性时间复杂度)。
   3.提出了一个路径长度递减的上限。我们的kSP查询算法的停止策略依赖于上界的单调递减性质。
   4.在真实数据集和合成数据集上的大量实验证实了该方法的优越性

2. Problem Definition
   Definition 3
   
   Definition 4
   

3. Computational Model
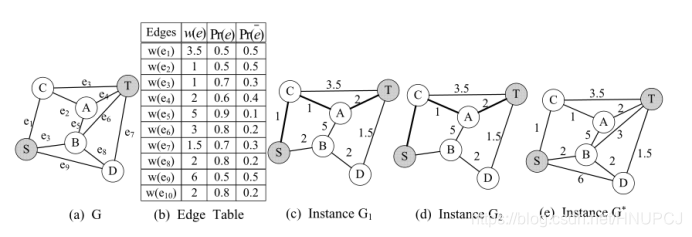
   给定一条路径P，P也指路径中的所有边。我们用E§来表示路径P存在的事件，即P中所有边都存在的事件。我们用Pr(E§)来表示事件E§发生的概率。因此，我们有以下关于Pr(E§)的等式
   
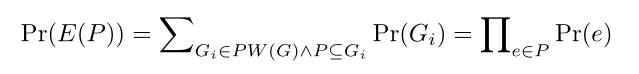
   进一步，我们还用E§来表示P不存在的事件，即P中并非所有边都存在的事件。形式上，我们有以下等式:
   
   1)给定不确定图G中的两个顶点S和T，P1表示G中从S到T的最短路径，即G的某个版本，P1是G中最短路径的事件等价于P1存在于G中的事件，因此，我们有如下等式
   
   所有情况之前最短的路径出现的概率即为该条路径为最短路径的概率
   2)让Pn表示G中S到T的第n条最短路径。Pn是G中最短路径的事件等价于Pn存在但路径Pn’都不存在的事件(n’= 1，…,n-1)因此，我们有以下方程
   
   为了计算等式，我们有以下过程:
   
   
   
   
   
   
   

4. Framework
   为了有效地回答一个kSP查询，我们采用了过滤-细化框架。具体来说，给定一个不确定图G中的两个顶点S和T以及一个参数k，我们首先找到kSP查询的所有候选路径。然后，对于每个候选路径Pn，我们通过等式6和7计算概率Pr(Pn= SP(G))，以找到答案。根据框架，有两个重要的问题需要解决:第一，我们需要高效地找到所有候选人，而不需要枚举从S到T的所有可能路径；第二，由于方程7的指数复杂性，直接对其求值非常昂贵。我们需要一种廉价的方法来评估Pr(Pn= SP(G))而不是包含-排除原理
   我们首先说明关于我们方法的直觉。给定从S到T的路径P，w§表示路径P的长度。当且仅当路径P存在且没有满足w(P’) < w§的P’存。虽然Pr(P = SP(G))的一般趋势是相对于w§递减，但Pr(P = SP(G))相对于w§不是单调递减的，如图2所示。
   
   为了高效地回答kSP查询，我们有以下步骤:
   1）给定路径P，求Pr(P = SP(G))的下界和上界，分别表示为LB(Pr(P = SP(G))和UB(Pr(P = SP(G))，其中UB(Pr(P = SP(G))相对于w§单调递减。图2展示了界限。
   
   以图2为例。为了找到前3条可能的最短路径，我们可以找到δ = UB(Pr(P4= SP(G))，因为有三条路径的下界大于δ。在这种情况下，对于任何路径Pi(i > 4)，UB(Pr(Pi= SP(G))) < δ。因此，可以安全地修剪所有路径Pi(i > 4)。
   3)为了提高查询性能，对于每个候选项，我们通过蒙特卡罗模拟计算Pr(Pi= SP(G))。

5. Probability Bounds
   给定一条路径Pn，即从S到T的第n条最短路径，我们讨论如何定义概率Pr(Pn= SP(G))的适当界限。
   5.1 The Lower Bound
   在这一小节中，我们讨论如何找到Pr(Pn= SP(G))的下界。当我们假设(P1-Pn)时，导出第一个下界，…，(Pn-1- Pn)没有公共边，其中(Pi-Pn)(i = 1，…n1)表示Pi中的所有边，但不表示Pn中的所有边。为了演示的目的，我们在下面的演示中将(Pi-Pn)称为路径，它指的是(Pi-Pn)中的所有边。如果这些路径(Pi-Pn)有许多公共边，则第一个下界不紧。为了解决这个问题，我们提出了一种近似的基于“集合覆盖”的方法(它具有线性时间复杂度)来评估下界。该下限有利于在(Pi-Pn)(I = 1，…，n-1)。
   
   
   
   
   
   The Second Lower Bound
   虽然LB1(Pr(Pn= SP(G)))为Pr(Pn= SP(G))提供了一个下界，但是当某些路径有很多公共边时，这个下界就不紧了。为了解决这个问题，我们引入了另一个基于集合覆盖问题的下界[12]。
   
   
   
   
   
   
   显然不可能枚举M上的所有集合覆盖，因为它的时间复杂度是指数的。我们建议寻找一些成对独立的集合覆盖。两个集合覆盖是成对独立的当且仅当它们没有公共边。
   
   首先，我们通过贪婪最小集覆盖算法[12]找到M上的集覆盖S。然后从M中去掉S中的所有边，在M上迭代以上步骤，直到M = φ或者找不到集合覆盖。这样就可以找到成对独立集覆盖S’1, …, S’m
   
   
   虽然我们可以用包含排除原理来计算Pr在等式10中，计算具有指数时间复杂度O(2m’)。除此之外，事件成对独立。我们提出了一种迭代算法来计算Pr具有线性时间复杂度。具体来说，我们有以下流程:
   
   
   ![在这里插入图片描述](https://img-blog.csdnimg.cn/20201129142225523.png
   
   
   5.2 The Upper Bound
   在这一小节中，我们讨论如何找到Pr(P = SP(G))的上界。根据第4节讨论的框架，上界必须随w§单调递减
   Pr(Pn= SP(G))的上限，定义如下: