2021-03-11

世界坐标系和相机坐标系的转换

在研究3D人体姿态估计的过程中，碰到了坐标系的转换问题，所以深入的研究和分析了一下这个部分的转换过程

世界坐标系主要是现实世界相机的位置，一般坐标原点在左相机或者右相机或者两个相机x轴方向的中心位置上面。

相机坐标系的坐标原点在光心的位置，Z轴垂直与光心所在平面。

所谓坐标系的转换其实也坐标系进行一个平移和旋转，坐标点在另外一个坐标系下的位置问题，本质上面坐标点的位置没有变换，只是点的坐标发生了变化。

世界坐标系和相机坐标系的转换问题：

首先介绍旋转过程。下图为世界坐标系绕z轴旋转模型：

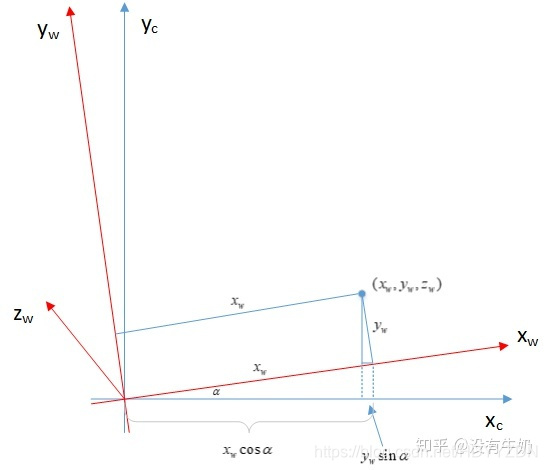
世界坐标系为Xw-Yw-Zw 相机坐标系为Xc-Yc-Zc ,当前一个世界坐标系中一个坐标点位置为 (Xw,Yw,Zw),在相机坐标系下Xc= ,Yc=,由于围绕z轴旋转，故 

,

写成矩阵的形式如下

其中，  3*3的变换矩阵称为 r1 。

同样的，可以得到关于x轴，y轴旋转的变换矩阵 r2， r3 。而总的旋转矩阵为R=r1*r2*r3 。

平移则相对简单，只需在旋转后的基础上加上一个平移量 ti即可。

综上，即可得世界坐标系到相机坐标系的变换为

 

R为旋转矩阵  即 为一个正交矩阵，正交矩阵的逆=正交矩阵的转置

那么利用 就可以得到Xw和Xc的关系了，也就是相机坐标系转化为世界坐标系

解析了我会利用空闲时间，将相应的python 代码附上，

如果有什么错误请踊跃指正。