算法导论学习笔记——32 字符串匹配

研究问题：

问目标串中能找出多少个模式串
解决方法与时间复杂度

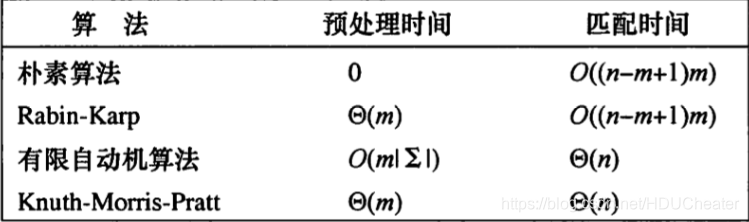
32.1朴素字符串匹配

就是以目标串中的每个元素为起点进行匹配，当匹配到模式串尾部，匹配成功，不然从下个元素重新匹配

32.2Rabin-Karp 算法

主要思想，通过预处理模式串与目标串第1到i个数之和对某个数的模，然后快速筛掉无效匹配

32.3 ac自动机

还没学，以后再补

32.4 Knuth-Morris-Pratt

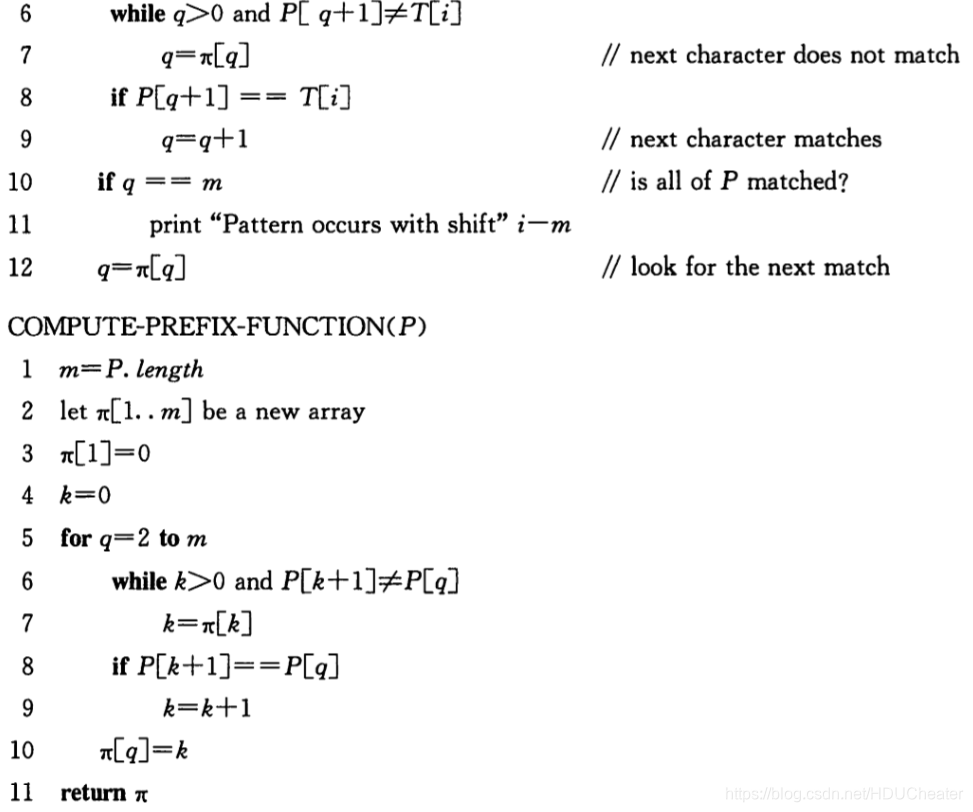
主要思想：
优化朴素的暴力匹配

为什么能优化暴力匹配？
举个例子:
目标串aaaaaaaaaaaaaaa，模式串aaaaaa
很容易观察到，模式串有大量相同的前后缀，
那么在用暴力匹配的方法去匹配的同时，
如果成功匹配了相同的后缀，那么下一次匹配就无需再从下一个字符开始重新匹配，而是可以从相同的前后缀的后一个字符开始匹配，从而节省时间

那么究竟要跳过多少个字符呢？
定义一个数组nex[i]，存储前i-1个元素里前缀与后缀匹配的最大值，即跳过的字符数
通过动态规划的方式，预处理出nex[i]

例子

vector<int>nex,ans;//nex[i]是前i-1个元素里前缀与后缀匹配的最大值
//ans存匹配成功的下标
string text,pattern;//pattern模式串，text目标串，在text中找pattern
void build(string pattern)
{
    int n=pattern.size();
    nex.resize(n+1);
    for(int i=0,j=nex[0]=-1;i<n;nex[++i]=++j)
        while(j!=-1&&pattern[j]!=pattern[i])
            j=nex[j];
}

然后就是匹配了

void match(string text,string pattern)
{
    ans.clear();
    int n=pattern.size(),m=text.size();
    build(pattern);
    for(int i=0,j=0;i<m;i++)
    {
        while(j>0&&text[i]!=pattern[j]) j=nex[j];
        if(text[i]==pattern[j]) j++;
        if(j==n) ans.push_back(i-n+1),j=nex[j];
    }
}

其他应用：
计算最长回文子串
题目链接：
设目标字符串长度为n
将目标字符串复制一份并反转，
合成新字符串s+#+s反，
利用上面的预处理，
计算出前后缀相同的nex[i]数组
nex[n]即为答案。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<long long,long long> pll;
template<class T>inline void rd(T &x){x=0;char o,f=1;while(o=getchar(),o<48)if(o==45)f=-f;do x=(x<<3)+(x<<1)+(o^48);while(o=getchar(),o>47);x*=f;}
const int inf=~0u>>2; 
const ll INF=~0ull>>2;
const int maxn=200000+10;
vector<int>nex;
int build(string pattern)
{
    int n=pattern.size();
    nex.resize(n+1);
    for(int i=0,j=nex[0]=-1;i<n;nex[++i]=++j)
        while(~j&&pattern[j]!=pattern[i])
            j=nex[j];
    return nex[n];
}
void solve()
{
	string s,t; cin>>s; int l=0,r=s.size()-1;
    while(s[l]==s[r]&&l<r) l++,r--;
    string t1=s.substr(0,l),t2=s.substr(r+1);
    s=s.substr(l,r-l+1); t=s; reverse(t.begin(),t.end());
    string a=s+'*'+t,b=t+'*'+s;
    string p=a.substr(0,build(a));
    string q=b.substr(0,build(b));
    cout<<t1<<(p.size()>q.size()?p:q)<<t2<<endl;
}
int main()
{
	#ifndef ONLINE_JUDGE
	freopen("hzh.in","r",stdin);
	//freopen("hzh.out","w",stdout);
	#endif
	ll T;
    rd(T);
    while(T--)
		solve();
    return 0;
}

补充：其它字符串匹配解法
1.马拉车（manacher）
2.哈希
3.PAM聚类算法