hdu2196——Computer

Computer

Time Limit: 1000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 3455    Accepted Submission(s): 1750

Problem Description

A school bought the first computer some time ago(so this computer's id is 1). During the recent years the school bought N-1 new computers. Each new computer was connected to one of settled earlier. Managers of school are anxious about slow functioning of the net and want to know the maximum distance Si for which i-th computer needs to send signal (i.e. length of cable to the most distant computer). You need to provide this information.


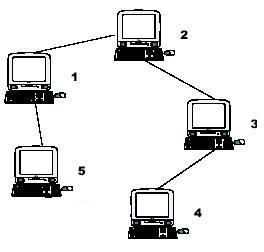
Hint: the example input is corresponding to this graph. And from the graph, you can see that the computer 4 is farthest one from 1, so S1 = 3. Computer 4 and 5 are the farthest ones from 2, so S2 = 2. Computer 5 is the farthest one from 3, so S3 = 3. we also get S4 = 4, S5 = 4.

 

Input

Input file contains multiple test cases.In each case there is natural number N (N<=10000) in the first line, followed by (N-1) lines with descriptions of computers. i-th line contains two natural numbers - number of computer, to which i-th computer is connected and length of cable used for connection. Total length of cable does not exceed 10^9. Numbers in lines of input are separated by a space.

 

Output

For each case output N lines. i-th line must contain number Si for i-th computer (1<=i<=N).

 

Sample Input

  

   5
1 1
2 1
3 1
1 1
  

 

Sample Output

  

   3
2
3
4
4
  

 

Author

scnu

 

Recommend

lcy   |   We have carefully selected several similar problems for you:   1561  1011  3456  2242  1059


显然连起来的图是一棵树，所以每个点离本身最远的一定是树直径的某一端

#include <set>
#include <map>
#include <list>
#include <stack>
#include <queue>
#include <vector>
#include <cmath>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 10010;

int dist1[N], dist2[N];
int head[N];
bool vis[N];
int ans, end_p, tot, n;
int a1, a2;

struct node
{
    int weight;
    int next;
    int to;
}edge[N << 2];

void addedge(int from, int to, int weight)
{
    edge[tot].to = to;
    edge[tot].weight = weight;
    edge[tot].next = head[from];
    head[from] = tot++;
}

void build()
{
    memset ( head, -1, sizeof(head) );
    tot = 0;
    int u, v, w;
    for (int i = 2; i <= n; ++i)
    {
        scanf("%d%d", &u, &w);
        addedge(i, u, w);
        addedge(u, i, w);
    }
}

void bfs(int v0, int dist[])
{
    queue <int> qu;
    memset (vis, 0, sizeof(vis) );
    while ( !qu.empty() )
    {
        qu.pop();
    }
    qu.push(v0);
    dist[v0] = 0;
    ans = 0;
    vis[v0] = 1;
    while ( !qu.empty() )
    {
        int u = qu.front();
        qu.pop();
        for (int i = head[u]; i != -1; i = edge[i].next)
        {
            int v = edge[i].to;
            if (!vis[v])
            {
                vis[v] = 1;
                dist[v] = dist[u] + edge[i].weight;
                qu.push(v);
                if(dist[v] > ans)
                {
                    ans = dist[v];
                    end_p = v;
                }
            }
        }
    }
}

int main()
{
    while (~scanf("%d", &n))
    {
        build();
        bfs(1, dist1);
        a1 = end_p;
        bfs(a1, dist1);
        a2 = end_p;
        bfs(a2, dist2);
        for (int i = 1; i <= n; ++i)
        {
            printf("%d\n", max(dist1[i], dist2[i]));
        }
    }
    return 0;
}