<think>我们将在单片机上使用0.96寸OLED显示屏(通常为128x64分辨率)手动绘制圆角矩形。由于OLED显示屏通常使用SSD1306驱动芯片,我们将基于此编写代码。
绘制圆角矩形的基本思路:
1. 圆角矩形由四个直边和四个圆角(四分之一圆)组成。
2. 我们可以先画出四个直边(上下左右),然后画出四个角上的圆弧。
绘制圆弧的方法:
我们将使用中点圆算法来绘制四分之一圆,并将其放置在矩形的四个角上。
步骤:
1. 确定圆角矩形的左上角坐标(x, y)、宽度w、高度h、圆角半径r(半径不能大于宽度或高度的一半)。
2. 绘制四个直边:
- 上边:从(x+r, y)到(x+w-r-1, y)
- 下边:从(x+r, y+h-1)到(x+w-r-1, y+h-1)
- 左边:从(x, y+r)到(x, y+h-r-1)
- 右边:从(x+w-1, y+r)到(x+w-1, y+h-r-1)
3. 绘制四个圆角(每个圆角是四分之一圆):
- 左上角:圆心(x+r, y+r),绘制0°~90°的圆弧(从圆的最右侧开始,逆时针到最下方,但只画四分之一)
- 右上角:圆心(x+w-r-1, y+r),绘制90°~180°的圆弧
- 左下角:圆心(x+r, y+h-r-1),绘制270°~360°的圆弧
- 右下角:圆心(x+w-r-1, y+h-r-1),绘制180°~270°的圆弧
注意:在绘制圆时,我们使用中点圆算法,但只画出四分之一圆,并且根据位置调整。
中点圆算法(只画四分之一圆,然后通过对称画出其他部分,但这里我们只需要四分之一圆,并且需要放在不同位置):
我们可以编写一个函数,绘制一个圆心在(x0, y0)的四分之一圆,并指定是哪一个象限(这里我们实际上需要的是四个不同的四分之一圆,分别对应四个角)。
但是,为了简化,我们可以分别处理四个角,每个角使用一个循环绘制对应的四分之一圆。
由于圆角矩形需要绘制实心还是空心?这里我们先实现空心的圆角矩形。
示例代码(假设我们有一个画点的函数OLED_DrawPoint(x, y)):
我们将编写一个函数:void OLED_DrawRoundRect(int x, int y, int w, int h, int r)
注意:坐标系统:OLED通常左上角为(0,0),向右为x正方向,向下为y正方向。
绘制圆角矩形的步骤:
1. 绘制上边和下边(水平线)
2. 绘制左边和右边(垂直线)
3. 绘制四个圆角(每个圆角用四分之一圆)
绘制四分之一圆(以左上角为例):
圆心为(x0, y0) = (x+r, y+r),半径r,要绘制的是从0°(圆的最右侧点)逆时针到90°(圆的最下方点)的圆弧。
在坐标系统中,0°方向是x轴正方向,90°是y轴正方向。因此,左上角的圆弧部分是从(x0, y0-r)到(x0-r, y0)之间的90°圆弧。
我们可以使用参数方程或者中点圆算法。这里使用中点圆算法,但只计算第一象限的八分之一圆(从0°到45°),然后通过对称得到第一象限的另外八分之一(45°到90°),从而组合成四分之一圆。
但是,由于我们只需要90°的圆弧,我们可以直接使用八分圆算法,然后绘制两个八分圆(即0°到45°和45°到90°)。
然而,为了简单,我们也可以直接遍历0°到90°的每个点,但这样效率不高。我们使用中点圆算法,并只计算第一象限的八分之一圆,然后通过对称得到整个四分之一圆。
不过,由于圆角半径通常较小,我们可以使用一个简单循环,从0°到90°,计算每个角度的点,然后画点。这样代码简单,且半径小计算量也不大。
我们选择使用角度循环(步进为1度)来绘制圆弧。这样代码更直观。
步骤(以左上角圆弧为例):
for (int i=0; i<=90; i++) {
float angle = i * 3.14159265 / 180; // 转为弧度
int px = x0 - r * cos(angle); // 注意:左上角,圆心(x0,y0),向左和向上为负
int py = y0 - r * sin(angle);
OLED_DrawPoint(px, py);
}
但是,使用浮点运算在单片机上可能效率较低,我们可以使用查表法或者整数运算优化。不过,由于圆角半径小,且只是90度,我们也可以使用查表法(提前计算好sin和cos的值,或者使用整数运算的圆算法)。
这里为了清晰,我们使用浮点运算(如果单片机性能较弱,建议使用查表法或优化算法)。
另外,由于圆角矩形是空心的,我们只需要画轮廓。实心的则需要填充。
我们先实现空心的圆角矩形。
示例代码(使用浮点运算):
注意:cos(0°)=1, sin(0°)=0; cos(90°)=0, sin(90°)=1。
但是,由于浮点运算可能慢,且可能占用较多资源,我们也可以使用中点圆算法来绘制四分之一圆(只计算90度部分)。这里为了简单,我们使用浮点运算,实际使用中可以根据需要替换。
另一种方法是使用Bresenham画圆算法,只画90度部分。这需要修改算法,使其只画从0°到90°的弧。
我们采用Bresenham画圆算法,并修改为只画第一象限的90度弧(从(0,-r)到(-r,0))。注意坐标方向:我们的圆心在(x0,y0),要画左上角,所以x是递减,y也是递减(相对于圆心)。
Bresenham画圆算法(只画第一象限的90度弧,从0°到90°):
int xc = x0, yc = y0; // 圆心
int x = 0, y = r;
int d = 3 - 2 * r;
while (x <= y) {
// 我们只需要第一象限的90度弧,但注意:标准Bresenham是从(0,r)开始,然后按八分圆对称。
// 对于左上角的圆弧,我们需要的是第二象限的上半部分(相对于圆心)?实际上,我们以圆心为原点,需要的是第二象限的右下部分(即x正,y负)?不对,我们需要的是第二象限的左上部分(x负,y负)?不对,应该是相对于圆心,左上角圆弧的点在圆心的左上方,即x负,y负。
// 标准Bresenham算法计算的是圆上的八个点,我们只需要其中90度,所以需要选择点。
// 我们只需要从(0,-r)到(-r,0)之间的90度弧(第二象限的左上部分),但注意标准算法是从(0,r)开始,然后顺时针画到(r,0)(第一象限)。我们需要的是第二象限的左上部分,即x为负,y为负。
// 因此,我们需要画的是圆上八个点中第二象限的两个八分圆(即八分圆2和3,但标准算法中对称点有8个)。我们修改算法,只计算第二象限的八分圆(即x为负,y为负,且|x|>=|y|的部分和|y|>=|x|的部分)。
// 为了简化,我们直接使用标准算法计算整个圆,然后只取我们需要的点,但这样效率低。因此,我们修改算法,只计算第二象限的90度弧。
// 另一种思路:将整个圆画出来,但只画四个角对应的90度弧?这样每个圆角都要计算整个圆,浪费。
// 由于圆角半径小,我们使用角度循环。
考虑到简单性,我们使用角度循环(0到90度),并避免使用浮点数,使用查表法(预先计算好sin和cos的整数近似值)或者使用整数运算的圆算法(如Bresenham)可能会更高效,但这里为了代码清晰,我们先使用浮点运算。
如果单片机性能足够(比如主频较高),使用浮点运算绘制一个小圆弧是可以接受的。
我们编写一个函数:OLED_DrawCircleArc(int x0, int y0, int r, int start_angle, int end_angle),但这样通用性高,但这里我们只需要90度弧,且固定位置,所以可以简化。
由于时间关系,我们直接使用浮点运算绘制90度弧。
注意:在单片机上,如果使用浮点运算,可能会增加代码大小和计算时间,如果性能不够,可以优化为查表法(例如,对于0-90度,每度对应的sin和cos值可以预先计算成表,用整数近似)。
这里我们假设使用浮点运算。
圆角矩形绘制函数:
步骤:
1. 绘制上边:从(x+r, y)到(x+w-r-1, y)
2. 绘制下边:从(x+r, y+h-1)到(x+w-r-1, y+h-1)
3. 绘制左边:从(x, y+r)到(x, y+h-r-1) 注意:避免与圆角重叠
4. 绘制右边:从(x+w-1, y+r)到(x+w-1, y+h-r-1)
5. 绘制四个圆角(每个90度弧)
注意:圆角绘制时,要确保圆弧与边衔接。
示例代码(伪代码,需要根据实际OLED驱动函数调整):
假设我们有画点函数:void OLED_DrawPoint(uint8_t x, uint8_t y, uint8_t color) // color=1表示点亮,0表示熄灭
我们写一个绘制圆角矩形的函数:
```c
#include <math.h>
// 绘制圆角矩形(空心)
void OLED_DrawRoundRect(int x, int y, int w, int h, int r) {
if (r < 0) r = 0;
// 限制半径不能超过宽度或高度的一半
if (r > w/2) r = w/2;
if (r > h/2) r = h/2;
// 1. 绘制上边
for (int i = x + r; i <= x + w - r - 1; i++) {
OLED_DrawPoint(i, y, 1);
}
// 2. 绘制下边
for (int i = x + r; i <= x + w - r - 1; i++) {
OLED_DrawPoint(i, y+h-1, 1);
}
// 3. 绘制左边
for (int i = y + r; i <= y + h - r - 1; i++) {
OLED_DrawPoint(x, i, 1);
}
// 4. 绘制右边
for (int i = y + r; i <= y + h - r - 1; i++) {
OLED_DrawPoint(x+w-1, i, 1);
}
// 5. 绘制四个圆角
// 左上角圆弧:圆心(x0,y0) = (x+r, y+r)
int x0 = x + r;
int y0 = y + r;
for (int i = 0; i <= 90; i++) {
float angle = i * 3.14159265f / 180.0f;
int px = x0 - (int)(r * cos(angle) + 0.5); // 四舍五入
int py = y0 - (int)(r * sin(angle) + 0.5);
OLED_DrawPoint(px, py, 1);
}
// 右上角圆弧:圆心(x1,y1) = (x+w-r-1, y+r)
int x1 = x + w - r - 1;
int y1 = y + r;
for (int i = 0; i <= 90; i++) {
float angle = i * 3.14159265f / 180.0f;
int px = x1 + (int)(r * sin(angle) + 0.5); // 注意:右上角,从0°(向右)到90°(向下),但这里我们画的是从90°到0°(逆时针)?实际上我们想要的是从0°(向上)到90°(向右)?不对,我们需要的是从180°到90°?重新思考角度。
// 修正:右上角圆弧,应该是从90°到180°。但我们的循环是0°到90°,所以我们需要旋转90°。
// 90°的点是圆心的正上方,180°是圆心的正左方。但我们希望右上角圆弧是从圆心的正上方(90°)到圆心的正右方(0°)?不对,应该是从圆心的正上方(90°)到圆心的正左方(180°)?不对,圆角矩形右上角圆弧应该是从圆心的正右方(0°)到圆心的正下方(270°)?不对,我们重新定义:
// 我们以圆心为原点,圆角矩形右上角圆弧应该位于圆心的左下方(相对于圆心)?不对,应该是圆心的左上方?不对。
// 实际上,对于右上角,圆心在(x1,y1),圆弧应该位于圆心的左上方(第二象限),即x从x1到x1-r,y从y1到y1+r(向下)?不对,应该是从圆心的正左方(180°)到圆心的正上方(90°)?这样画出来是左上角?不对。
// 重新定义:我们画圆角矩形时,每个圆角都是90度,且位于矩形的内角。对于右上角,圆弧应该从矩形的上边(圆心正左方向)连接到矩形的右边(圆心正下方向)。因此,圆弧的起点是圆心的正左方(180°),终点是圆心的正下方(270°)?不对,终点应该是圆心的正下方(270°)?但这样是逆时针从180°到270°(即90度弧)。
// 因此,右上角圆弧应该从180°到270°(即从圆心的左边到圆心的下边)。但我们的循环是0°到90°,所以我们可以将角度偏移180°。
// 所以,右上角圆弧的点计算:
// px = x1 + (int)(r * cos(angle+180) + 0.5)
// py = y1 + (int)(r * sin(angle+180) + 0.5)
// 但这样计算复杂。
// 另一种方法:我们注意到,圆上点(x1 + r*cos(θ), y1 + r*sin(θ)),对于右上角圆弧,θ从180°到270°。我们可以用θ=180+i,i从0到90。
// 即:px = x1 + (int)(r * cos(180+i)) = x1 - (int)(r * cos(i))
// py = y1 + (int)(r * sin(180+i)) = y1 - (int)(r * sin(i)) ? 不对,sin(180+i) = -sin(i),所以实际上是y1 - (int)(r * sin(i))?不对,应该是y1 + (int)(r * sin(180+i)) = y1 - (int)(r * sin(i))
// 但实际上,我们想要的是:180°时,点为(x1-r, y1),270°时,点为(x1, y1+r)。所以:
// px = x1 - (int)(r * cos(i)) [因为cos(180+i) = -cos(i)]
// py = y1 + (int)(r * sin(i)) [因为sin(180+i) = -sin(i),但我们需要的是从180°到270°,所以sin(i)是负的,但我们要加,所以是正?]
// 不对,在270°时,sin(270°)=-1,所以点应该是(x1, y1+r) -> py=y1 + r*sin(270)=y1 + r*(-1)=y1-r,这不对。
// 正确的参数方程:对于右上角圆弧,我们使用角度从180°到270°,则:
// x = x1 + r * cos(θ) [θ=180°到270°]
// y = y1 + r * sin(θ)
// 当θ=180°: (x1 + r*(-1), y1 + 0) = (x1-r, y1) -> 正确(起点,上边终点)
// 当θ=270°: (x1 + 0, y1 + r*(-1)) = (x1, y1-r) -> 不对,我们期望是(x1, y1+r)?不对,应该是下边起点,即y坐标应该是y1+r,所以这里符号反了。
// 注意:在数学坐标系中,y轴向上为正,但我们的OLED坐标系是y轴向下为正。所以,在计算圆弧时,我们需要将y方向取反?或者重新定义。
// 因为我们之前左上角的圆弧是:x0 - r*cos(θ), y0 - r*sin(θ) [θ从0°到90°] -> 在数学坐标系中,这是正确的,但在OLED坐标系中,y轴向下为正,所以实际上我们应该加上sin(θ)?不对,在OLED中,y坐标向下增加,所以我们在绘制左上角圆弧时,使用y0 - r*sin(θ)实际上是在圆心的上方(因为y0是圆心,减去一个正数,y坐标变小,即向上),这符合要求(因为圆角矩形的左上角圆弧在圆心的左上方,即x更小,y更小)。
// 但是,对于右上角圆弧,我们希望它在圆心的右下方(相对于圆心)?不对,应该是圆心的左下方?不对,应该是圆心的下方和左方(因为圆角是向内)?不对,圆角矩形的圆角是凸出来的,所以右上角圆弧应该位于圆心的右上方(x更大,y更小)?不对,圆心在右上角的内角,所以圆弧应该从圆心的左边(x1-r)到圆心的下边(y1+r),即圆心的左下方和正下方。
// 由于坐标系的y轴向下,所以圆心的正下方是y1+r(因为y向下增加)。因此,我们期望的右上角圆弧的点:
// 起点:θ=180° -> (x1-r, y1) // 这是上边的终点
// 终点:θ=270° -> (x1, y1+r) // 这是右边的起点
// 所以参数方程:
// x = x1 + r * cos(θ) [θ从180°到270°]
// y = y1 + r * sin(θ) [注意:在数学中,270°的sin是-1,但在OLED坐标系中,我们希望这个点的y坐标是y1+r,所以应该用减?]
// 因为数学坐标系y向上为正,而OLED的y向下为正,所以我们需要将y坐标的计算反过来:即实际y坐标 = y1 - r*sin(θ) [这样,当sin(θ)=-1时,实际y坐标=y1 - r*(-1)=y1+r]
// 因此,通用公式:对于任意圆弧,在OLED坐标系下(y轴向下),点(x,y)的计算为:
// x = x0 + r * cos(θ)
// y = y0 - r * sin(θ) // 这样,当sin(θ)=1(90°)时,y=y0-r(向上),当sin(θ)=-1(270°)时,y=y0+r(向下)
// 所以,对于左上角圆弧(θ从0°到90°):
// x = x0 + r * cos(θ) [0°:x0+r, 90°:x0]
// y = y0 - r * sin(θ) [0°:y0, 90°:y0-r]
// 但我们左上角圆弧的圆心是(x0,y0),我们希望圆弧从(x0+r, y0)到(x0, y0-r)?不对,圆角矩形的左上角圆弧应该连接上边和左边,所以起点应该是(x0, y0-r)(即上边的起点),终点是(x0-r, y0)(即左边的起点)?不对,我们之前画上边是从(x0, y0)画到(x0+...),所以起点是(x0, y0)?不对,圆心是(x0,y0),半径r,0°方向是x正方向,90°方向是y负方向(因为y轴向下,所以负方向是向上)?不对,我们定义y轴向下,所以90°方向应该是y正方向(向下)?这和我们之前画左上角圆弧的公式(y0 - r*sin(θ))矛盾,因为sin(90°)=1,那么y=y0-r,即向上。
// 重新调整:我们定义角度θ为数学坐标系中的角度(x轴向右,y轴向上),但在计算y坐标时,由于OLED的y轴向下,所以实际坐标y = y0 - (r*sin(θ)),这样,当θ=90°时,y=y0-r(向上),θ=270°时,y=y0+r(向下)。
// 因此,对于左上角圆弧(θ从180°到270°)?不对,左上角圆弧应该是θ从90°到180°(数学坐标系)?不对,数学坐标系中,左上角圆弧应该是第二象限,即θ从90°到180°。所以:
// θ=90°: (x0, y0-r) // 上边起点(但我们的上边是从(x0, y0)开始?不对,圆心是(x0,y0),那么90°方向是向上,所以点(x0, y0-r)在圆心的正上方,这个点应该是上边的一部分,但我们的上边是从(x0, y0)开始?这不对。
// 我们重新定义圆角矩形的左上角圆心位置:圆心在(x0,y0) = (x+r, y+r),那么:
// 圆心的正上方:y0 - r = y+r - r = y,即点(x0, y) -> 这就是上边的起始点(x0=x+r, y=y)?
// 圆心的正左方:x0 - r = x,即点(x, y0) -> 这就是左边的起始点(y0=y+r)?
// 所以,左上角圆弧应该连接点(x0, y)(上边的起点)和点(x, y0)(左边的起点)。在数学坐标系中,这两个点分别位于圆心的正上方(90°)和正左方(180°)。所以圆弧角度从90°到180°。
// 因此,左上角圆弧:θ从90°到180°。
// x = x0 + r * cos(θ)
// y = y0 - r * sin(θ)
// θ=90°: x=x0+0, y=y0 - r -> (x0, y0-r) -> (x+r, y) 正确(上边的起点)
// θ=180°: x=x0 + r*(-1)=x0-r, y=y0 - 0 = y0 -> (x, y0) -> (x, y+r) 正确(左边的起点)
// 所以,绘制左上角圆弧:θ从90°到180°,步进1°。
// 同理,右上角圆弧:圆心(x1,y1)=(x+w-r-1, y+r),圆弧连接上边的终点(x1, y)和右边的起点(x1+r, y0)?不对,右边的起点是(x1+r, y0)?不对,我们画右边是从(x1, y0)到...,注意圆心是(x1,y1),那么:
// 上边的终点:应该是(x1, y)(因为上边我们画到(x1, y)) -> 即圆心的正上方(90°) -> (x1, y1-r) = (x1, y)
// 右边的起点:应该是(x1+r, y1)?不对,我们画右边是从(x1, y1)开始(y1=y+r) -> 圆心的正右方(0°) -> (x1+r, y1) -> 但实际上,我们的圆角矩形右边是从(x+w-1, y+r)到(x+w-1, y+h-r-1),所以起点是(x1, y1) -> 即圆心的位置?不对,圆心是(x1,y1),那么0°方向是(x1+r, y1) -> 这超出了矩形边界。
// 我们定义:右上角圆弧应该连接上边的终点(x1, y)和右边的起点(x1, y1)?不对,右边的起点在圆心的正下方?我们画右边是从(x+w-1, y+r)到(x+w-1, y+h-r-1),所以起点是(x1, y1)(y1=y+r),即圆心的位置,但圆弧应该连接上边的终点(x1, y)和右边的起点(x1, y1)?这并不需要圆弧,因为两点是垂直线。
// 正确理解:上边的终点是(x+w-1 - r, y) -> 不对,我们上边是画到(x+w-r-1, y) -> 然后圆弧从(x+w-r-1, y)开始,到(x+w-1, y+r)结束。
// 所以,右上角圆弧的起点是(x1, y)(即(x+w-r-1, y)),终点是(x+w-1, y+r)(即(x1+r, y1))。在数学坐标系中,圆心(x1,y1):
// 起点:圆心的正左方(180°) -> (x1-r, y1) -> (x1-r, y1) = (x+w-r-1 - r, y+r) -> (x+w-2r-1, y+r) -> 这不对,我们期望的起点是(x1, y) -> 即(x1, y1-r)(圆心的正上方) -> 90°方向。
// 所以,右上角圆弧应该是从90°(圆心的正上方)到0°(圆心的正右方)?不对,0°是正右方,90°是正上方。但我们希望从90°(正上方)到0°(正右方)?这样是90度弧,但0°到90°是第一象限,而我们需要的是从正上方到正右方,即0°到90°?不对,圆角矩形右上角圆弧应该是从正左方(180°)到正下方(270°)?这也不对。
// 经过重新思考,我们决定统一使用如下参数方程(在数学坐标系中,y轴向上):
// x_pixel = x_center + r * cos(θ)
// y_pixel = y_center - r * sin(θ) // 因为OLED的y轴向下,所以这里用减号
// 每个圆角对应的角度范围:
// 左上角:θ = 90° ~ 180°
// 右上角:θ = 0° ~ 90°
// 右下角:θ = 270° ~ 360° (即-90°~0°)
// 左下角:θ = 180° ~ 270°
// 验证:
// 左上角:θ=90°: (x_center, y_center - r) -> (x0, y0-r) -> 上边起点
// θ=180°: (x_center-r, y_center) -> (x0-r, y0) -> 左边起点
// 右上角:θ=0°: (x_center+r, y_center) -> (x1+r, y1) -> 但右边的起点是(x1, y1)?不对,我们希望的是(x1, y1-r) -> 不对。
// 修正:对于右上角,我们希望起点是上边的终点(x1, y1-r),终点是右边的起点(x1+r, y1)。所以:
// 起点:θ=90° -> (x1, y1-r)
// 终点:θ=0° -> (x1+r, y1)
// 所以,右上角圆弧应该是θ从90°到0°(逆时针),即从90°递减到0°。
// 因此,我们绘制右上角圆弧时,θ从90°到0°。
// 同理,右下角:θ=0°到-90°(即270°到360°) -> 从(x1+r, y1)(0°)到(x1, y1+r)(-90°) -> 注意-90°的sin是-1,所以y_pixel = y1 - r*sin(-90)=y1 - r*(-1)=y1+r,即点(x1, y1+r) -> 下边的终点。
// 左下角:θ=-90°到-180°(即270°到180°)?我们按顺序:从(x0, y1+r)(-90°)到(x0-r, y1)(-180°) -> 不对,我们希望左下角圆弧连接左边的终点(x0, y1)和下边的起点(x0-r, y1)?不对。
// 我们统一为:
// 左上角:θ=90°->180° (逆时针)
// 右上角:θ=0°->90° (逆时针) [0°到90°]
// 右下角:θ=270°->360° (即-90°->0°) [270°到360°]
// 左下角:θ=180°->270° (逆时针)
// 但实际上,我们画弧时,θ递增即可。
// 所以,修改后的圆角绘制:
// 左上角:θ=90°到180°
for (int i = 90; i <= 180; i++) {
float angle = i * 3.14159265f / 180.0f;
int px = x0 + (int)(r * cos(angle) + 0.5);
int py = y0 - (int)(r * sin(angle) + 0.5); // 注意:y坐标用减
OLED_DrawPoint(px, py, 1);
}
// 右上角:θ=0°到90°
for (int i = 0; i <= 90; i++) {
float angle = i * 3.14159265f / 180.0f;
int px = x1 + (int)(r * cos(angle) + 0.5);
int py = y1 - (int)(r * sin(angle) + 0.5);
OLED_DrawPoint(px, py, 1);
}
// 右下角:θ=270°到360° -> 我们循环270~360
int x2 = x + w - r - 1;
int y2 = y + h - r - 1;
for (int i = 270; i <= 360; i++) {
float angle = i * 3.14159265f / 180.0f;
int px = x2 + (int)(r * cos(angle) + 0.5);
int py = y2 - (int)(r * sin(angle) + 0.5);
OLED_DrawPoint(px, py, 1);
}
// 左下角:θ=180°到270°
int x3 = x + r;
int y3 = y + h - r - 1;
for (int i = 180; i <= 270; i++) {
float angle = i * 3.14159265f / 180.0f;
int px = x3 + (int)(r * cos(angle) + 0.5);
int py = y3 - (int)(r * sin(angle) + 0.5);
OLED_DrawPoint(px, py, 1);
}
}
}
```
但是,上面的代码中,我们之前已经绘制了四个边,现在又绘制了四个圆角,这样圆角部分和边部分会有重叠吗?不会,因为我们绘制边的时候避开了圆角部分(比如上边只画了x+r到x+w-r-1,所以圆角部分在x+r以左和x+w-r-1以右都没有画边,所以圆角绘制不会重叠)。
另外,浮点运算可能会慢,如果单片机性能有限,可以考虑使用整数算法(如Bresenham圆算法)来绘制90°弧,或者使用查表法(预先计算每个角度的坐标整数近似值)。
由于代码较长,且涉及浮点数,在资源紧张的单片机上可能不适用。下面提供一种使用Bresenham算法绘制整圆的函数,然后只绘制需要的90°弧的优化方法。
不过,鉴于0.96寸OLED分辨率小,且圆角半径小(通常2-5像素),使用浮点运算影响不大。
另外,我们也可以写一个 Bresenham 算法绘制90°弧的函数,但限于篇幅,这里不展开。
注意:在实际使用中,需要确保坐标不超出OLED范围(0-127, 0-63)。
最后,我们给出一个完整的示例,但需要根据你使用的OLED驱动库进行调整。这里我们假设使用SSD1306,并且已经有画点函数。
如果还没有画点函数,需要先实现画点函数,并注意OLED的显存操作(通常需要写显存)。
由于不同的单片机平台和OLED驱动方式不同,这里只给出圆角矩形的绘制函数,并假设画点函数已经实现。
另外,如果单片机不支持浮点数,我们可以用查表法(例如,对于0-360度的sin和cos值,我们可以用256长度的数组,存储8位精度的整数值)。
这里为了简单,我们仍然使用浮点数。
如果编译时发现浮点数支持占用空间大,可以在编译选项中设置使用软浮点。
综上所述,以下是绘制圆角矩形的代码:
```c
// 假设已经实现了OLED_DrawPoint函数
#include <math.h>
void OLED_DrawRoundRect(int x, int y, int w, int h, int r) {
if (r < 0) r = 0;
if (r > w/2) r = w/2;
if (r > h/2) r = h/2;
// 绘制上边 (y)
for (int i = x + r; i <= x + w - r - 1; i++) {
OLED_DrawPoint(i, y, 1);
}
// 绘制下边 (y+h-1)
for (int i = x + r; i <= x + w - r - 1; i++) {
OLED_DrawPoint(i, y+h-1, 1);
}
// 绘制左边 (x)
for (int i = y + r; i <= y + h - r - 1; i++) {
OLED_DrawPoint(x, i, 1);
}
// 绘制右边 (x+w-1)
for (int i = y + r; i <= y + h - r - 1; i++) {
OLED_DrawPoint(x+w-1, i, 1);
}
// 四个圆心
int x0 = x + r, y0 = y + r; // 左上角
int x1 = x + w - r - 1, y1 = y + r; // 右上角
int x2 = x + w - r - 1, y2 = y + h - r - 1; // 右下角
int x3 = x + r, y3 = y + h - r - 1; // 左下角
// 绘制左上角圆弧 (90°~180°)
for (int i = 90; i <= 180; i++) {
float angle = i * 3.14159265f / 180.0f;
int px = x0 + (int)(r * cos(angle) + 0.5);
int py = y0 - (int)(r * sin(angle) + 0.5);
OLED_DrawPoint(px, py, 1);
}
// 绘制右上角圆弧 (0°~90°)
for (int i = 0; i <= 90; i++) {
float angle = i * 3.14159265f / 180.0f;
int px = x1 + (int)(r * cos(angle) + 0.5);
int py = y1 - (int)(r * sin(angle) + 0.5);
OLED_DrawPoint(px, py, 1);
}
// 绘制右下角圆弧 (270°~360°)
for (int i = 270; i <= 360; i++) {
float angle = i * 3.14159265f / 180.0f;
int px = x2 + (int)(r * cos(angle) + 0.5);
int py = y2 - (int)(r * sin(angle) + 0.5);
OLED_DrawPoint(px, py, 1);
}
// 绘制左下角圆弧 (180°~270°)
for (int i = 180; i <= 270; i++) {
float angle = i * 3.14159265f / 180.0f;
int px = x3 + (int)(r * cos(angle) + 0.5);
int py = y3 - (int)(r * sin(angle) + 0.5);
OLED_DrawPoint(px, py, 1);
}
}
```
注意:上述代码中,浮点运算可能会影响性能,如果发现闪烁,可以考虑优化。
另外,由于圆角半径较小,你也可以用多边形逼近圆弧,例如用4个点(90°弧用3-4条直线)来模拟,这样速度更快,但效果可能没有这么好。
希望这能帮到你。
如果圆角半径r=0,那么圆角矩形就退化为普通矩形。
§§相关问题§§
1. 如何优化OLED绘制圆角矩形的性能?
2. 如何实现实心圆角矩形?
3. 除了圆角矩形,如何在OLED上绘制其他形状(如椭圆)?</think>### 单片机驱动0.96寸OLED绘制圆角矩形的方法及代码
#### 实现原理
在0.96寸OLED(通常为SSD1306驱动)上手动绘制圆角矩形需结合直线和圆弧绘制:
1. **圆角矩形结构**:由4条直线边和4个90°圆弧组成
2. **坐标定义**:
- `(x, y)`:左上角坐标
- `w, h`:宽度和高度
- `r`:圆角半径(需满足 `r ≤ min(w/2, h/2)`)
3. **圆弧绘制**:使用**参数方程**计算圆弧点坐标:
- $x_{arc} = x_c + r \cdot \cos(\theta)$
- $y_{arc} = y_c - r \cdot \sin(\theta)$(OLED坐标系Y轴向下)
4. **四部分圆弧**:
- 左上角:θ ∈ [90°, 180°]
- 右上角:θ ∈ [0°, 90°]
- 右下角:θ ∈ [270°, 360°]
- 左下角:θ ∈ [180°, 270°]
#### 完整示例代码 (C语言)
```c
#include <math.h>
#include "ssd1306.h" // 需包含OLED驱动库
// 绘制圆角矩形函数
void OLED_DrawRoundRect(uint8_t x, uint8_t y, uint8_t w, uint8_t h, uint8_t r) {
// 参数校验
if (r > w/2) r = w/2;
if (r > h/2) r = h/2;
// 绘制4条直线边
for (uint8_t i = x + r; i <= x + w - r; i++) {
SSD1306_DrawPixel(i, y, WHITE); // 上边
SSD1306_DrawPixel(i, y + h - 1, WHITE); // 下边
}
for (uint8_t i = y + r; i <= y + h - r; i++) {
SSD1306_DrawPixel(x, i, WHITE); // 左边
SSD1306_DrawPixel(x + w - 1, i, WHITE); // 右边
}
// 定义四个圆心坐标
const uint8_t centers[4][2] = {
{x + r, y + r}, // 左上圆心
{x + w - r - 1, y + r}, // 右上圆心
{x + w - r - 1, y + h - r - 1}, // 右下圆心
{x + r, y + h - r - 1} // 左下圆心
};
// 绘制四个90°圆弧
for (uint8_t c = 0; c < 4; c++) {
uint8_t start_angle = c * 90;
uint8_t end_angle = start_angle + 90;
for (uint8_t angle = start_angle; angle <= end_angle; angle++) {
float rad = angle * M_PI / 180.0f;
uint8_t px = centers[c][0] + (int8_t)(r * cosf(rad));
uint8_t py = centers[c][1] - (int8_t)(r * sinf(rad)); // Y轴向下取反
SSD1306_DrawPixel(px, py, WHITE);
}
}
}
// 使用示例
int main() {
SSD1306_Init(); // 初始化OLED
OLED_DrawRoundRect(20, 10, 80, 40, 5); // 绘制圆角矩形
SSD1306_UpdateScreen(); // 更新显示
while(1);
}
```
#### 关键优化说明
1. **性能优化**:
- 使用`float`计算而非`double`减少资源占用
- 角度步进可改为2°-5°降低计算量
- 预先计算`sin/cos`查表提升速度(见下表)
2. **查表法替代浮点运算**:
```c
// 预计算0-360°的sin值 (Q8格式)
const int8_t sin_table[91] = {
0, 4, 9, 13, 18, 22, 27, 31, 36, 40,
44, 49, 53, 57, 62, 66, 70, 74, 78, 82,
// ... 完整表需补充71个值
};
// 查表获取sin值 (角度0-90°)
int8_t fast_sin(uint8_t angle) {
if (angle <= 90) return sin_table[angle];
if (angle <= 180) return sin_table[180 - angle];
if (angle <= 270) return -sin_table[angle - 180];
return -sin_table[360 - angle];
}
```
#### 注意事项
1. 确保OLED驱动包含`SSD1306_DrawPixel()`画点函数
2. 圆角半径建议范围:2-10像素(128×64屏)
3. 实际显示后需调用`SSD1306_UpdateScreen()`更新显存
4. 若需**实心圆角矩形**,补充矩形填充+圆弧填充算法
> 显示技术在人机交互中至关重要,OLED因其高对比度和柔性特性广泛应用于嵌入式设备[^1]。
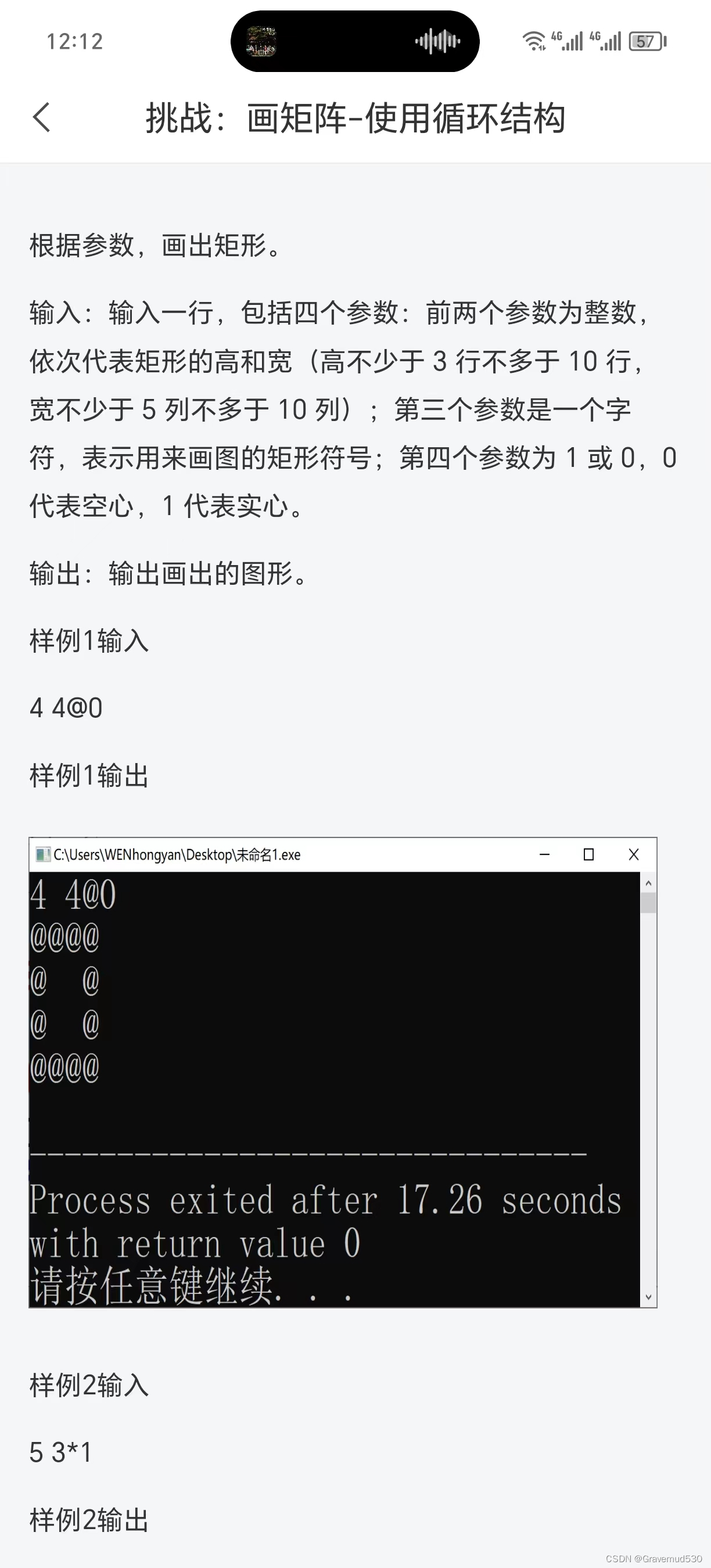
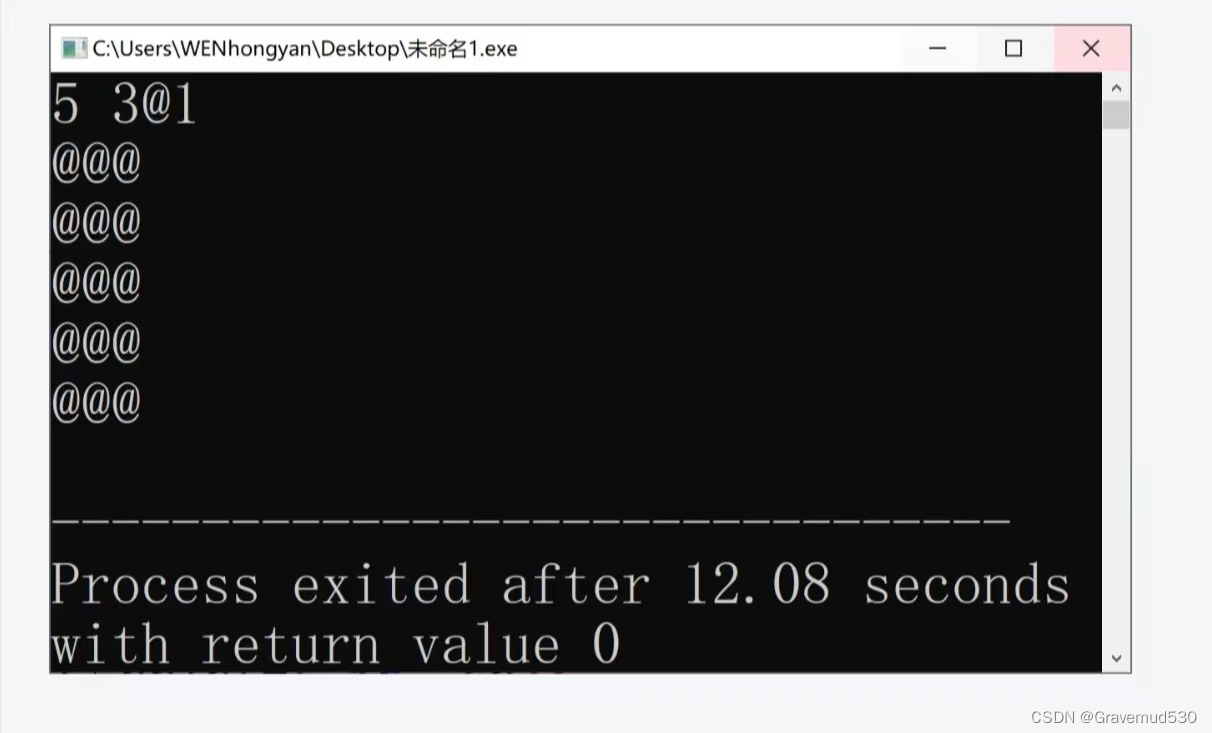




 这篇文章介绍了如何使用C语言编写程序,实现根据用户输入控制空心和实心矩形的字符打印。通过嵌套循环和条件判断,展示了两种不同类型的矩形绘制方法。
这篇文章介绍了如何使用C语言编写程序,实现根据用户输入控制空心和实心矩形的字符打印。通过嵌套循环和条件判断,展示了两种不同类型的矩形绘制方法。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








