My Batis

1.创建项目时，需要添加两个依赖
（1）MyBatis Framework
（2）MySQL Driver

2.在application.properties里面设置数据库的相关连接信息

3.设置mybatis相关信息

先再resource里面创建一个文件夹：mybatis
mybatis.mapper-locations=classpath:mybatis/*Mapper.xml 这里的mybatis是在resource里面创建的一个文件夹的名字，要对应
mybatis.configuration.log-impl=org.apache.ibatis.logging.stdout.StdOutImpl
logging.level.com.example.demo=debug

4.配置xml文件

<?xml version="1.0" encoding="UTF-8"?>
<!DOCTYPE mapper PUBLIC "-//mybatis.org//DTD Mapper 3.0//EN" "http://mybatis.org/dtd/mybatis-3-mapper.dtd">
<mapper namespace=""></mapper>

使用MyBatis实现增、删、改、查功能

①查询userinfo表中的所有用户信息

在接口中定义方法

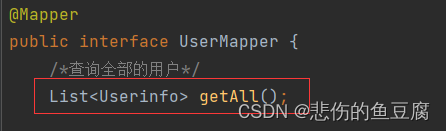
在xml中实现接口，查询使用<select>标签

id：是接口中定义的方法的名称

resultType是这个方法的返回类型，这个类型为userinfo，将这个类型的路径方法resultType中

②根据Id进行查询

（1）使用#{}获取数据

此时id的类型在数据库中定义为int，传递时必需使用包装类定义

在xml中实现取数据时，此时的id和Param里面的要对应，并且Param里面的要和数据库对应

（2）使用${}获取数据

#{}和${}的区别：

Ⅰ：${}在控制台打印的sql语句，直接将数据进行替换，读取时及时执行

#{}在控制台打印的sql语句，预执行，将代码中要输入的参数变成" ？"占位符

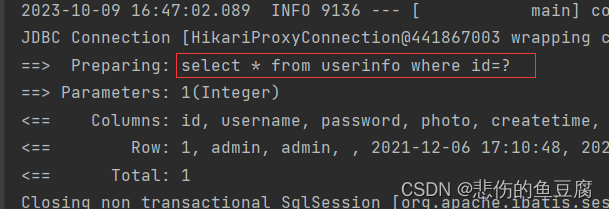
Ⅱ：${}不安全，存在sql注入；#{}是安全的，不存在sql注入

结论：#{}虽然是安全的，但是不能完全替代${}

${} 的使用场景：当业务需要进行传递SQL命令时，只能使用${}，不能是哦也能够#{}，但是使用了${}，那么传递的参数一定要被穷举，否则不能被使用

③根据Id进行删除，删除返回的类型是受影响的行数，所以方法的返回结果用int接受

删除可以不用设置resultType

在测试delUserById这个方法时，如果想要测试业务但是并不想影响数据库的内容，可以在测试方法上加上注释@Transactional

④根据用户id进行修改，返回的结果也是受影响的行数

传递的是一个userinfo对象，在xml中取其中的参数也是用#{}进行读取

⑤插入一个新的用户，返回的结果是一个受影响的行数

⑥like查询

在使用like查询的时候，在xml文件中不能够使用#{}来读取数据

like的SQL语句：select * from userinfo where username like '% 三 %';

因为#{}是预执行，它会认为"% 三 %"是一个值，所以执行报错。使用${}读取时，是可以完成相应的要求的，但是${}会存在SQL注入，并且使用${}的前提是可以被穷举的，所以此时两个方法都不合适

采用数据库内置的函数：concat()来实现。