C++数据结构·线段树

原创已于 2025-08-19 09:58:02 修改 · 2.7k 阅读

45 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #c++ #线段树

于 2025-08-19 09:57:43 首次发布

C++ 同时被 2 个专栏收录

23 篇文章

订阅专栏

C++数据结构

8 篇文章

订阅专栏

线段树 $(S e g m e n t$ $T ree)$ 定义

本质与用途

线段树是一种 二叉树数据结构，用于高效处理 区间查询（如求和、最值）和 区间更新 操作，所有操作均可在 O(log n) 时间内完成。

核心特性

结构特性

每个节点代表一个区间 [l, r]
叶子节点：区间长度为1（存储原始数据）
非叶子节点：存储子区间的 合并结果（如区间和、最值）

操作支持

操作类型	时间复杂度	典型应用
区间查询	O(log n)	求和、求最大值/最小值
单点更新	O(log n)	修改单个元素值
区间更新	O(log n)	懒标记（Lazy Tag）优化

与普通树的区别

特性	线段树	普通二叉树
节点含义	区间范围+统计值	数据值+左右指针
构建目的	高效区间操作	数据层次化存储
存储方式	数组模拟完全二叉树	动态节点或指针链接

经典问题适配性

适合场景

动态区间统计（实时查询/更新）
离线查询（先处理所有更新再查询）
值域较大时需结合 离散化

不适用场景

全量数据频繁重建（直接数组更高效）
非区间类问题（如单点频繁随机访问）

可视化理解

         [1,6]=21
        /       \
    [1,3]=6     [4,6]=15
     /    \      /    \
 [1,2]=3 [3]=3 [4,5]=9 [6]=6
  /    \       /    \
[1]=1 [2]=2 [4]=4 [5]=5

叶子节点：原始数据 [1,2,3,4,5,6]
非叶子节点：存储子区间和（如 [1,3] 的值为 1+2+3=6）

关键点：线段树的本质是 用空间换时间,通过预处理区间信息将查询/更新复杂度从 $O (n)$ 优化到 $O (l o g n)$

模板代码

先讲线段树建立

struct Tree{
	int date;//维护值,下方子树的和 
	int l,r;//左右端点 
	int lz_tag;//懒标记 
}c[MAXN*4];//线段树

这里先建立一个c(即线段树)
接下来讲正经的建树

void build(int node,int l,int r){//建树
	//node表示节点,l表示左端点,r表示右端点
	if(l==r){
		//叶子节点,储存原始数据 
		c[node].date=a[l];
		c[node].l=l;
		c[node].r=r;
		//储存数据 
	}else{
		int mid=(l+r)/2;//中间点 
		build(node*2,l,mid);//左子树(l~mid)
		build(node*2+1,mid+1,r);//右子树(mid+1~r)
		c[node].date=c[node*2].date+c[node*2+1].date;
		//维护左子节点和右子节点的值
		c[node].l=l;
		c[node].r=r;
		//记录左、右端点 
	}
}

代码里有注释
给个例图

         [1,6]=21
        /       \
    [1,3]=6     [4,6]=15
     /    \      /    \
 [1,2]=3 [3]=3 [4,5]=9 [6]=6   --->以上都是非叶子节点
  /    \       /    \
[1]=1 [2]=2 [4]=4 [5]=5    --->叶子节点

原理就是用叶子节点储存原始数据
然后用父节点储存子节点的数据
本质是用数组实现完全二叉树
接下来是下传懒标记

void lztag_k(int node,int k){
    //将node节点上的懒标记+k
    c[node].lz_tag+=k;
    c[node].date+=k*(c[node].r-(c[node].l-1));
} 
void pushdown(int node){
    //下传懒标记
    if(c[node].lz_tag==0)//不存在懒标记 
        return;
    lztag_k(node*2,c[node].lz_tag);//左子节点 
    lztag_k(node*2+1,c[node].lz_tag);//右子节点 
    c[node].lz_tag=0;
}

用于高效处理区间更新操作
避免每次递归到叶子节点
将时间复杂度从 $O (n)$ 优化到 $O (l o g$ $n)$
还有线段树的关键2个函数！
$s u m$ 和 $u p d a t e$
区间查询和区间修改/更新
$s u m :$

int sum(int node,int l,int r){
    //计算l~r区间和
    if(l<=c[node].l&&c[node].r<=r){
        return c[node].date;
        //当前区间在要求区间内 
    } 
    pushdown(node);//下传懒标记
    int mid=(c[node].l+c[node].r)/2;//中间点 
    int answer=0;
    if(l<=mid){
        answer+=sum(node*2,l,r);//左子节点的值 
    }
    if(mid+1<=r){
        answer+=sum(node*2+1,l,r);//右子节点的值 
    }
    return answer;
}

线段树本质是把一个区间分成多个区间储存便于递归计算
所以只需找左子节点和右子节点
$u p d a t e :$

void update(int node,int l,int r,int k){
    //将区间[l,r]+k
    if(l<=c[node].l&&c[node].r<=r){
        c[node].date+=(c[node].r-(c[node].l-1))*k;
        //计算公式:date=区间长度*k
        c[node].tag+=k;//懒tag更新
        return; 
    }
    pushdown(node);
    int mid=(c[node].l+c[node].r)/2;//中间点 
    if(l<=mid){
        update(node*2,l,r,k);//更新左子节点
    }
    if(mid+1<=r){
        update(node*2+1,l,r,k);//更新右子节点
    }
    c[node].date=c[node*2].date+c[node*2+1].date;
    //当前节点的值=左子节点的值+右子节点的值
}

OK完事看懂了后，来道例题

例题传送

模板线段数1

P3372 【模板】线段树 1

题目描述

如题，已知一个数列 ${a_i\}$ ，你需要进行下面两种操作：

将某区间每一个数加上 $k$ 。
求出某区间每一个数的和。

输入格式

第一行包含两个整数 $n, m$ ，分别表示该数列数字的个数和操作的总个数。

第二行包含 $n$ 个用空格分隔的整数 $a_i$ ，其中第 $i$ 个数字表示数列第 $i$ 项的初始值。

接下来 $m$ 行每行包含 $3$ 或 $4$ 个整数，表示一个操作，具体如下：

1 x y k：将区间 $[x, y]$ 内每个数加上 $k$ 。
2 x y：输出区间 $[x, y]$ 内每个数的和。

输出格式

输出包含若干行整数，即为所有操作 2 的结果。

输入输出样例 #1

输入 #1

输出 #1

11
8
20

说明/提示

对于 $15\%$ 的数据： $\le 8$ ， $\le 10$ 。
对于 $35\%$ 的数据： $\le {10}^3$ ， $\le {10}^4$ 。
对于 $100\%$ 的数据： $\le n, m \le {10}^5$ ， $a_i,k$ 为正数，且任意时刻数列的和不超过 $2\times 10^{18}$ 。

【样例解释】

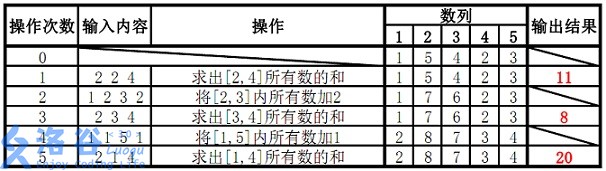
分析

~~都标了时候模板线段树分析个damn~~
先看要求
给出数列长度和操作次数
输入数列
$m$ 行操作

操作1：将区间 $l$ ~ $r$ 内的所有值 $+ k$
操作2：输出区间 $l$ ~ $r$ 内的所有值的和

经典的线段树模板
直接看数据范围
注意线段树4倍空间

AC代码

注释版：

#include <bits/stdc++.h>
using namespace std;
#define int long long 
const int MAXN=4e5;
struct Tree{
    int date;//维护值,下方子树的和 
    int l,r;//左右端点 
    int lz_tag;//懒标记 
}c[MAXN];//线段树 
int a[MAXN
];//数列 
void build(int node,int l,int r){//建树
	//node表示节点,l表示左端点,r表示右端点
	if(l==r){
		//叶子节点,储存原始数据 
		c[node].date=a[l];
		c[node].l=l;
		c[node].r=r;
		//储存数据 
	}else{
		int mid=(l+r)/2;//中间点 
		build(node*2,l,mid);//左子树(l~mid)
		build(node*2+1,mid+1,r);//右子树(mid+1~r)
		c[node].date=c[node*2].date+c[node*2+1].date;
		//维护左子节点和右子节点的值
		c[node].l=l;
		c[node].r=r;
		//记录左、右端点 
	}
}
void lztag_k(int node,int k){
    //将node节点上的懒标记+k
    c[node].lz_tag+=k;
    c[node].date+=k*(c[node].r-(c[node].l-1));
} 
void pushdown(int node){
    //下传懒标记
    if(c[node].lz_tag==0)//不存在懒标记 
        return;
    lztag_k(node*2,c[node].lz_tag);//左子节点 
    lztag_k(node*2+1,c[node].lz_tag);//右子节点 
    c[node].lz_tag=0;
}
int sum(int node,int l,int r){
    //计算l~r区间和
    if(l<=c[node].l&&c[node].r<=r){
        return c[node].date;
        //当前区间在要求区间内 
    } 
    pushdown(node);//下传懒标记
    int mid=(c[node].l+c[node].r)/2;//中间点 
    int answer=0;
    if(l<=mid){
        answer+=sum(node*2,l,r);//左子节点的值 
    }
    if(mid+1<=r){
        answer+=sum(node*2+1,l,r);//右子节点的值 
    }
    return answer;
}
void update(int node,int l,int r,int k){
    //将区间[l,r]+k
    if(l<=c[node].l&&c[node].r<=r){
        c[node].date+=(c[node].r-(c[node].l-1))*k;
        //计算公式:date=区间长度*k
        c[node].lz_tag+=k;//懒tag更新
        return; 
    }
    pushdown(node);
    int mid=(c[node].l+c[node].r)/2;//中间点 
    if(l<=mid){
        update(node*2,l,r,k);//更新左子节点
    }
    if(mid+1<=r){
        update(node*2+1,l,r,k);//更新右子节点
    }
    c[node].date=c[node*2].date+c[node*2+1].date;
    //当前节点的值=左子节点的值+右子节点的值
}
signed main(){
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>a[i];
    build(1,1,n);//建树 
    for(int i=1;i<=m;i++){
        int op;
        cin>>op;
        if(op==1){//操作1 
            int l,r,k;
            cin>>l>>r>>k;
            update(1,l,r,k);
            //区间修改 
        }else{//操作2 
            int l,r;
            cin>>l>>r;
            cout <<sum(1,l,r)<<endl;
            //区间查询 
        }
    }
    return 0;
}//刚好100行awa

无注释版：

#include <bits/stdc++.h>
using namespace std;
#define int long long 
const int MAXN=4e5;
struct Tree{
    int date;
    int l,r;
    int lz_tag;
}c[MAXN];
int a[MAXN];
void build(int node,int l,int r){
	if(l==r){
		c[node].date=a[l];
		c[node].l=l;
		c[node].r=r;
	}else{
		int mid=(l+r)/2;
		build(node*2,l,mid);
		build(node*2+1,mid+1,r);
		c[node].date=c[node*2].date+c[node*2+1].date;
		c[node].l=l;
		c[node].r=r;
	}
}
void lztag_k(int node,int k){
    c[node].lz_tag+=k;
    c[node].date+=k*(c[node].r-(c[node].l-1));
} 
void pushdown(int node){
    if(c[node].lz_tag==0)
        return;
    lztag_k(node*2,c[node].lz_tag);
    lztag_k(node*2+1,c[node].lz_tag);
    c[node].lz_tag=0;
}
int sum(int node,int l,int r){
    if(l<=c[node].l&&c[node].r<=r){
        return c[node].date;
    } 
    pushdown(node);
    int mid=(c[node].l+c[node].r)/2;
    int answer=0;
    if(l<=mid){
        answer+=sum(node*2,l,r);
    }
    if(mid+1<=r){
        answer+=sum(node*2+1,l,r);
    }
    return answer;
}
void update(int node,int l,int r,int k){
    if(l<=c[node].l&&c[node].r<=r){
        c[node].date+=(c[node].r-(c[node].l-1))*k;
        c[node].lz_tag+=k;
        return; 
    }
    pushdown(node);
    int mid=(c[node].l+c[node].r)/2;
    if(l<=mid){
        update(node*2,l,r,k);
    }
    if(mid+1<=r){
        update(node*2+1,l,r,k);
    }
    c[node].date=c[node*2].date+c[node*2+1].date;
}
signed main(){
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>a[i];
    build(1,1,n);
    for(int i=1;i<=m;i++){
        int op;
        cin>>op;
        if(op==1){
            int l,r,k;
            cin>>l>>r>>k;
            update(1,l,r,k);
        }else{
            int l,r;
            cin>>l>>r;
            cout <<sum(1,l,r)<<endl;
        }
    }
    return 0;
}