💫坚持坚持,养成习惯,持之以恒地学习。<( ̄︶ ̄)↗[GO!]
📆学习日期:2025年1月30日22:16:03
💻学习内容:快乐数 | 代码随想录
⏲️学习时长:1h
练习题目1
题目描述
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」 定义为:
- 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
- 然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。
- 如果这个过程 结果为 1,那么这个数就是快乐数。
如果 n 是 快乐数 就返回 true ;不是,则返回 false 。
示例 1:
输入:n = 19
输出:true
解释:
1^2 + 9^2 = 82
8^2 + 2^2 = 68
6^2 + 8^2 = 100
1^2 + 0^2 + 0^2 = 1示例 2:
输入:n = 2
输出:false提示:
1 <= n <= 231 - 1
解题思路1
- 整体思路&&注意事项
- 取数值各个位置上的单数之和 重点
- 使用哈希结构
set来判断sum是否已经重复出现(说明不是快乐数)
- sum出现过,说明已经进入循环,此时可判断
n不是快乐数
- 代码实现
class Solution {
public:
int getSum(int n){
int sum=0;
while(n){
sum=sum+(n%10)*(n%10);//取个位,求平方
n=n/10;//更新
}
return sum;
}
bool isHappy(int n) {
int sum;
unordered_set<int> set;
while(1){
sum=getSum(n);
if(sum==1){
return true;
}
//如果sum出现过,说明已经进入循环
if(set.find(sum)!=set.end()){
return false;
}
else {
set.insert(sum);//记录新的sum
}
n=sum;
}
}
};解题思路2
作者:金字塔下的小蜗牛
来源:力扣(LeetCode)
解题思路:
方法:
使用 “快慢指针” 思想,找出循环:“快指针” 每次走两步,“慢指针” 每次走一步,当二者相等时,即为一个循环周期。此时,判断是不是因为 1 引起的循环,是的话就是快乐数,否则不是快乐数。
注意:此题不建议用集合记录每次的计算结果来判断是否进入循环,因为这个集合可能大到无法存储;另外,也不建议使用递归,同理,如果递归层次较深,会直接导致调用栈崩溃。不要因为这个题目给出的整数是 int 型而投机取巧。
class Solution {
public:
int bitSquareSum(int n) {
int sum = 0;
while(n > 0)
{
int bit = n % 10;
sum += bit * bit;
n = n / 10;
}
return sum;
}
bool isHappy(int n) {
int slow = n, fast = n;
do{
slow = bitSquareSum(slow);
fast = bitSquareSum(fast);
fast = bitSquareSum(fast);
}while(slow != fast);
return slow == 1;//检查是否由 1 引起循环
}
};
// 作者:金字塔下的小蜗牛
// 链接:https://leetcode.cn/problems/happy-number/solutions/21454/shi-yong-kuai-man-zhi-zhen-si-xiang-zhao-chu-xun-h/
// 来源:力扣(LeetCode)
// 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。学习总结
- 取数值各个位置上的单数之和 重点
- 例如 水仙花数 等相似题目
int getSum(int n){
int sum=0;
while(n){
sum=sum+(n%10)*(n%10);//取个位,求平方
n=n/10;//更新
}
return sum;
}- 除了使用集合
set判断进入循环,是否有其他的解法? 待思考
- 快慢指针法(与环形链表的思路相似) 待思考| 202. 快乐数 - 力扣(LeetCode)
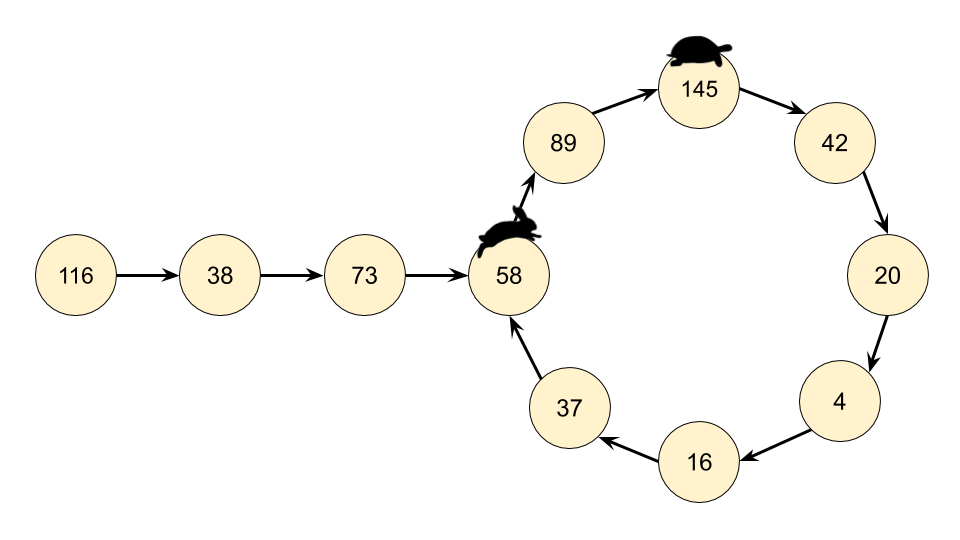
- 使用快慢指针法,空间复杂度为
O(1),这是因为没有使用集合。





















 476
476

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








