代码随想录算法训练营第三十七天|738.单调递增的数字、968.监控二叉树

day37 2023/03/09

一、单调递增的数字

给定一个非负整数 N，找出小于或等于 N 的最大的整数，同时这个整数需要满足其各个位数上的数字是单调递增。

（当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时，我们称这个整数是单调递增的。）

分析如下：
 

题目要求小于等于N的最大单调递增的整数，那么拿一个两位的数字来举例。

例如：98，一旦出现strNum[i - 1] > strNum[i]的情况（非单调递增），首先想让strNum[i - 1]--，然后strNum[i]给为9，这样这个整数就是89，即小于98的最大的单调递增整数。

这一点如果想清楚了，这道题就好办了。

此时是从前向后遍历还是从后向前遍历呢？

从前向后遍历的话，遇到strNum[i - 1] > strNum[i]的情况，让strNum[i - 1]减一，但此时如果strNum[i - 1]减一了，可能又小于strNum[i - 2]。

这么说有点抽象，举个例子，数字：332，从前向后遍历的话，那么就把变成了329，此时2又小于了第一位的3了，真正的结果应该是299。

那么从后向前遍历，就可以重复利用上次比较得出的结果了，从后向前遍历332的数值变化为：332 -> 329 -> 299

确定了遍历顺序之后，那么此时局部最优就可以推出全局，找不出反例，试试贪心。

代码如下：

class Solution {
public:
    int monotoneIncreasingDigits(int n) {
      string str=to_string(n);
      int flag=str.size();
      for(int i=str.size()-1;i>0;i--)
      {
          if(str[i-1]>str[i])
          {
              flag=i;
              str[i-1]--;
          }
      }
      for(int i=flag;i<str.size();i++)
      {
          str[i]='9';
      }
      return stoi(str);
      
    }
};

二、监控二叉树

给定一个二叉树，我们在树的节点上安装摄像头。

节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。

计算监控树的所有节点所需的最小摄像头数量。

分析如下：

我们发现题目示例中的摄像头都没有放在叶子节点上！

这是很重要的一个线索，摄像头可以覆盖上中下三层，如果把摄像头放在叶子节点上，就浪费的一层的覆盖。

所以把摄像头放在叶子节点的父节点位置，才能充分利用摄像头的覆盖面积。

从下往上看，局部最优：让叶子节点的父节点安摄像头，所用摄像头最少，整体最优：全部摄像头数量所用最少！

此时需要状态转移的公式，大家不要和动态的状态转移公式混到一起，本题状态转移没有择优的过程，就是单纯的状态转移！

来看看这个状态应该如何转移，先来看看每个节点可能有几种状态：

有如下三种：

• 该节点无覆盖
• 本节点有摄像头
• 本节点有覆盖

我们分别有三个数字来表示：

• 0：该节点无覆盖
• 1：本节点有摄像头
• 2：本节点有覆盖

主要有如下四类情况：

• 情况1：左右节点都有覆盖

左孩子有覆盖，右孩子有覆盖，那么此时中间节点应该就是无覆盖的状态了。

如图：

 

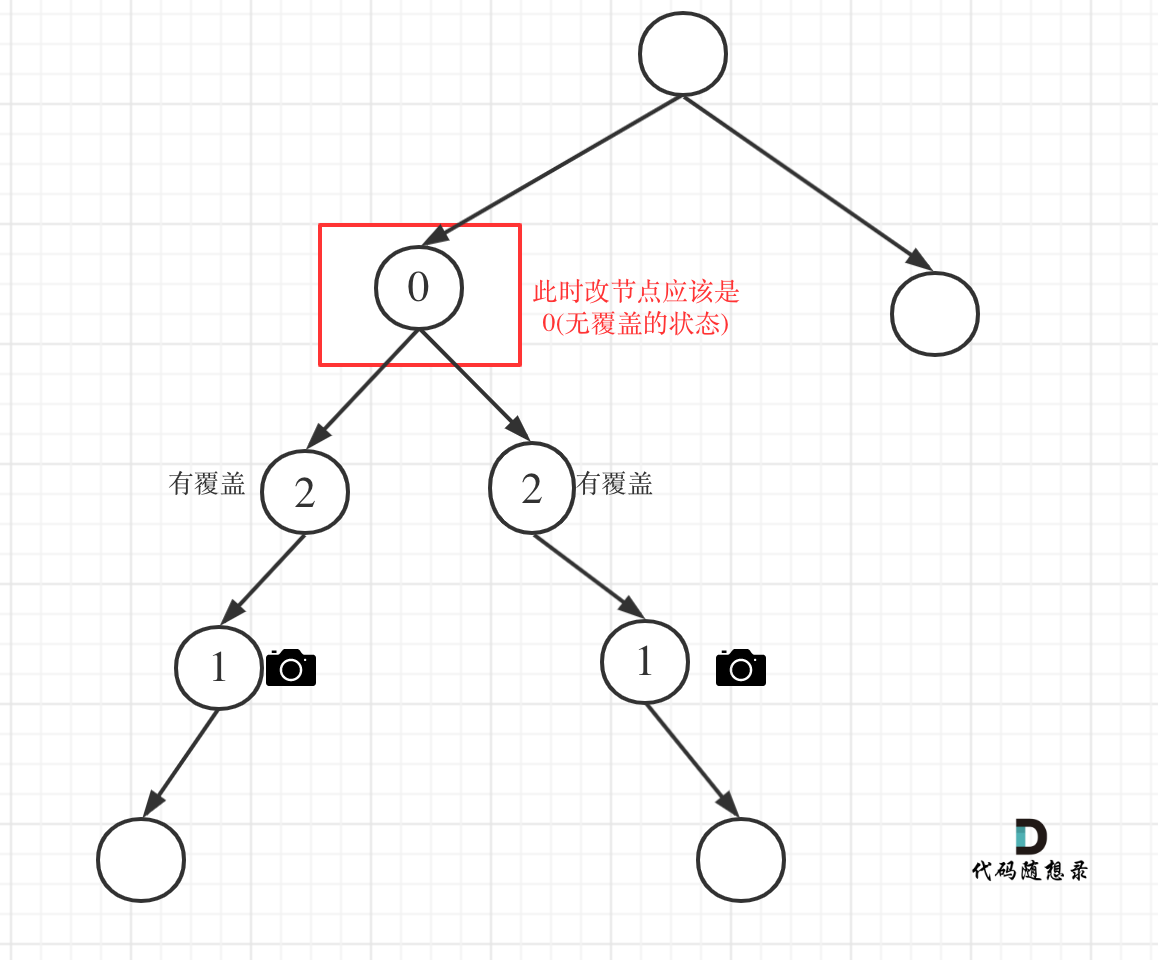
 左右节点至少有一个无覆盖的情况

左右节点至少有一个有摄像头

头结点没有覆盖

代码如下：

class Solution {
public:
    int result;
    int traversal(TreeNode* cur)
    {
        if(cur==NULL) return 2;
        int left=traversal(cur->left);
        int right=traversal(cur->right);
        if(left==2&&right==2) return 0;
        if(left==0||right==0) 
        {
            result++;
            return 1;
        }
        if(left==1||right==1) return 2;
        return -1;

    }
    int minCameraCover(TreeNode* root) {
       result=0;
       if(traversal(root)==0)
       {
           result++;
       }   
       return result;
    }
};