论文｜Node2vec算法原理、代码实战和在微信朋友圈的应用

1 概述

Node2vec是2016年斯坦福教授 Jure Leskovec、Aditya Grover提出的论文，论文的下载链接为：https://arxiv.org/pdf/1607.00653.pdf。

其本质上是对Deepwalk的延伸，也是属于图神经网络种随机游走模型一类。不了解Deepwalk的可以看上一篇文章：论文｜DeepWalk的算法原理、代码实现和应用说明。

Node2vec在DeepWalk的基础上提出了更加合理的图特征学习方法，提出了用于网络中可伸缩特征学习的半监督算法，使用SGD优化一个自定义的基于图的目标函数，该方法可以最大化的在D维特征空间保留节点的网络领域信息；在随机游走的基础上设计了一种二阶随机游走的过程，相当于对DeepWalk算法的一种扩展，它保留了邻居节点的图特征。

2 算法原理

2.1 学习框架

论文中将网络中的特征学习问题看作是一个极大似然优化问题，设 $G=(V,E)$为给定的网络，$f:V\Rightarrow {\mathbb{R}}^d$ 为节点到特征表征的映射函数，我们的目标是学习一个后续节点的预测任务，这里的 $d$ 表示的是节点的表征向量维度，$f$ 是一个 $|V|\ast d$ 的矩阵，同时为每个源节点 $u\in V$，定义 $N_s(u)\subset V$ 的网络邻居节点的社区抽样策略。

节点的表征学习目标函数为最大化节点 $u$ 的网络观测邻域 $N_s(u)$：
$$maxf\sum u\in VlogPr(N_s(u)|f(u))$$
但是基于上面的目标函数进行优化，是比较困难的，因此作者做了两点假设：

• 条件独立性假设：即假设结点间相互独立，简单来说就是，对于某一个源结点，其采用到的邻居结点是独立的，采用其中一个邻居结点不会对其他邻居结点造成影响
  $$\mathrm{Pr}\left(N_S(u)|f(u)\right)=\prod _{n_i\in N_S(u)}\mathrm{Pr}\left(n_i|f(u)\right)$$

• 特征空间对称假设：源结点和邻居结点的特征空间有一个对称性影响。简单来说就是，一个源结点和其某一个邻居结点有关系，那么对于这个邻居结点来说，这个源结点也是其邻居结点，影响是相互的
  $$\mathrm{Pr}\left(n_i|f(u)\right)=\frac{\exp \left(f\left(n_i\right)\cdot f(u)\right)}{{\sum }_{v\in V}\exp (f(v)\cdot f(u))}$$

根据以上两个假设，最终目标函数 $f$ 可以优化为以下形式：
$$\max f\sum u\in V\left[-\log Z_u+\sum _{n_i\in N_S(u)}f\left(n_i\right)\cdot f(u)\right]$$
由于归一化因子 $Z_u={\sum }_{v\in V}\exp (f(u)\cdot f(v))$，对于大型网络来说，计算成本很高，所以采用负采样技术进行优化，在定义特征函数 $f$ 模型参数上，采用随机梯度上升法对公式最终的目标函数进行优化。

2.2 搜索策略

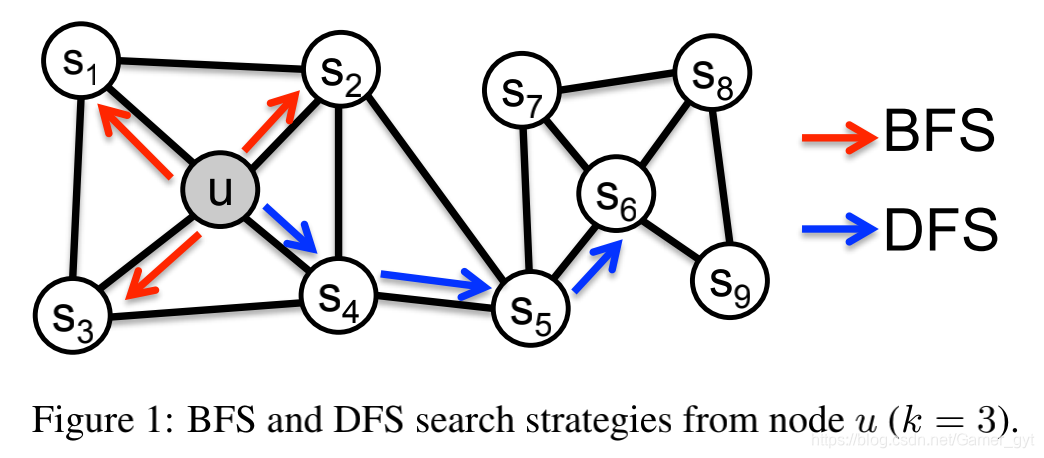
可以将采样源节点邻域问题视为一种网络局部搜索问题，所熟知的无非就是广度优先遍历（BFS）和深度优先遍历（DFS），广度优先更容易采样邻居节点，从而获得每个节点邻居的微观视图，这更容易表示结构的相似性，比如限制一个 $k=3$ 邻居域，节点 $u$ 的BFS就会对 $s1,s2,s3$ 采样，广度优先遍历采样邻居节点往往重复对此采样，这有利于减少偏差。对深度优先遍历来说，它尽可能深的遍历网络，采样节点更准确的反映了邻居节点的宏观情况，这更容易表示内容相似性，即验证同质性假设，而 $u$ 使用DFS就会对 $s4,s5,s6$ 进行采样。

2.3 Node2vec

a）随机游走策略

作者根据BFS和DFS的思想设计了一种灵活的带有偏重的随机游走策略，使BFS和DFS能够平滑地融入此策略中。

给定一个源节点 $u$，要进行步长为 $l$ 的随机游走，$c_i$ 表示游走序列中第 $i$ 个节点$c_0=u$，节点 $c_i$ 由以下分布产生：
$$p(c_i=x|c_{i-1}=v)=\{\begin{array}{c}\frac{{\pi }_{vx}}{Z},if(v,x)\in E\\ 0,otherwise\end{array}$$
其中：

• ${\pi }_{vx}$ 表示从节点 $v$ 到 节点 $x$ 的转移概率
• $Z$ 为归一化常量

定义由参数 $p$ 和参数 $q$ 引导的二阶随机游走如下：

如图假设随机游走序列由节点 $t$ 经过了边 $(t,v)$，现在要决定节点 $v$ 的下一步游走方向，所以需要评估出边 $(v,x)$ 上的转移概率 ${\pi }_{vx}$，并将转移概率最大的边作为下一步游走的方向，设边 $(v,x)$ 上的权值为 $w_{vx}$，则转移概率
$$a_{pq}(t,x)=\{\begin{array}{cc}\frac{1}{p}& if{d}_{tx}=0\\ 1& if{d}_{tx}=1\\ \frac{1}{q}& if{d}_{tx}=2\end{array}$$

从直观上可以看出，参数 $p$ 和 $q$ 控制的是游走序列向外探索和离开原来邻居节点的速率，特别的是当 $p=q=1$ 时，Node2vec的二阶随机游走的采样策略与Deepwak的随机游走策略一致。下面详解参数 $p$ 和参数 $q$ 在二阶随机游走所起到的作用：

• 返回参数 $p$ ： 参数 $p$ 控制在随机游走立即重新访问一个节点的可能性。当 $p$ 取值很大时$(p>max(q,1))$，控制往回游走的概率就会相对较小，这样重新对已经访问过的进行访问的可能性就会更小，这样的策略可以鼓励往外进行探索并且避免跳到已访问节点造成的冗余。另一方面，若当 $p$ 的值很小 $(p<min(q,1))$ 时，游走序列将会很大的概率一直围绕源节点 $u$ 的邻居进行采样，这样十分有益于描述一个节点与其邻居节点之间的关系（同质性）

• 进出参数 $q$ ： 参数 $q$ 可以在游走路径的搜索过程中区分“向内”和“向外”的节点。当参数 $q>1$时，随机游走就会更偏向于朝向那些之前访问过节点很近的节点，这样的策略有助于我们获得源节点 $u$ 的局部视图，在局部范围内，这种策略更像是BFS（结构性）。相反的，如果 $q<1$，那么游走序列会离之前访问过的点越来越远，这种向外探索的策略更像是DFS（同质性）

b）嵌入向量的产生

Node2vec算法是将获得的游走序列当作一种特殊的语料，使用基于Negative sampling的Skip-gram模型来产生嵌入向量。该部分内容和Word2vec介绍中的一致！

从输入层到隐藏层：
$$h=W_{k,.}^T:=v_{w_I}^T$$
从隐藏层到输出层：
$$p(w_{c,j}=w_{O,c}|w_I)=y_{c,j}=\frac{exp(u_{c,j})}{{\sum }_{j^{\prime }=1}^{V}exp(u_{j^{\prime }})}$$
其中：

• $w_I$ 表示的是输入词
• $w_{c,j}$ 表示输出层第$c$个词实际落在了第$j$个神经元
• $w_{O,c}$ 表示输出层第$c$个词应该落在第$O$个神经元
• $y_{c,j}$ 表示输出层第$c$个词实际落在了第$j$个神经元上归一化后的概率
• $u_{c,j}$ 表示输出层第$c$个词实际落在了第$j$个神经元上未归一化的值

因为输出层共享权重，所以：
$$u_{c,j}=u_j=(v_{w_j}^{\prime }{)}^T\ast h,forc=1,2,...,C$$
其中 $v_{w_j}^{\prime }$ 表示第$j$个单词的输出向量，其值为输出权重矩阵$W^{\prime }$的第$j$ 列。

损失函数变为：
$$\begin{gathered} E=-logp(w_{O,1},w_{O,2},..,w_{O,C}|w_I) \\ =-log\prod _{c=1}^C\frac{exp(u_{c,j_c^{\ast }})}{{\sum }_{j^{\prime }=1}^{V}exp(u_{j^{\prime }})} \\ =-\sum _{c=1}^C{u}_{j_c^{\ast }}+C\ast log\sum _{j^{\prime }=1}^{V}exp(u_{j^{\prime }}) \end{gathered}$$

注意⚠️

• 经验上一般选择使用skip-gram模型，因为效果较好
• 在Word2vec模型中，如果选择使用CBOW时，最终产出的word embedding为 单词的输出向量（$W_{N\ast V}^{\prime }$）表示，如果选择使用skip-gram时，最终产出的word embedding为单词的输入向量（$W_{N\ast V}$）表示，因为更倾向于选择靠近中心词一端的权重矩阵。

c）Node2vec算法过程

Node2vec的算法流程如下：

3 实验说明

3.1 Case 研究：基于《悲惨世界》

作者使用一个基于小说《悲惨世界》中的角色作为节点构建的网络，其中包含了77个节点和254个边。

其中生成的节点embedding表示为16维，聚类使用的是K-Means。

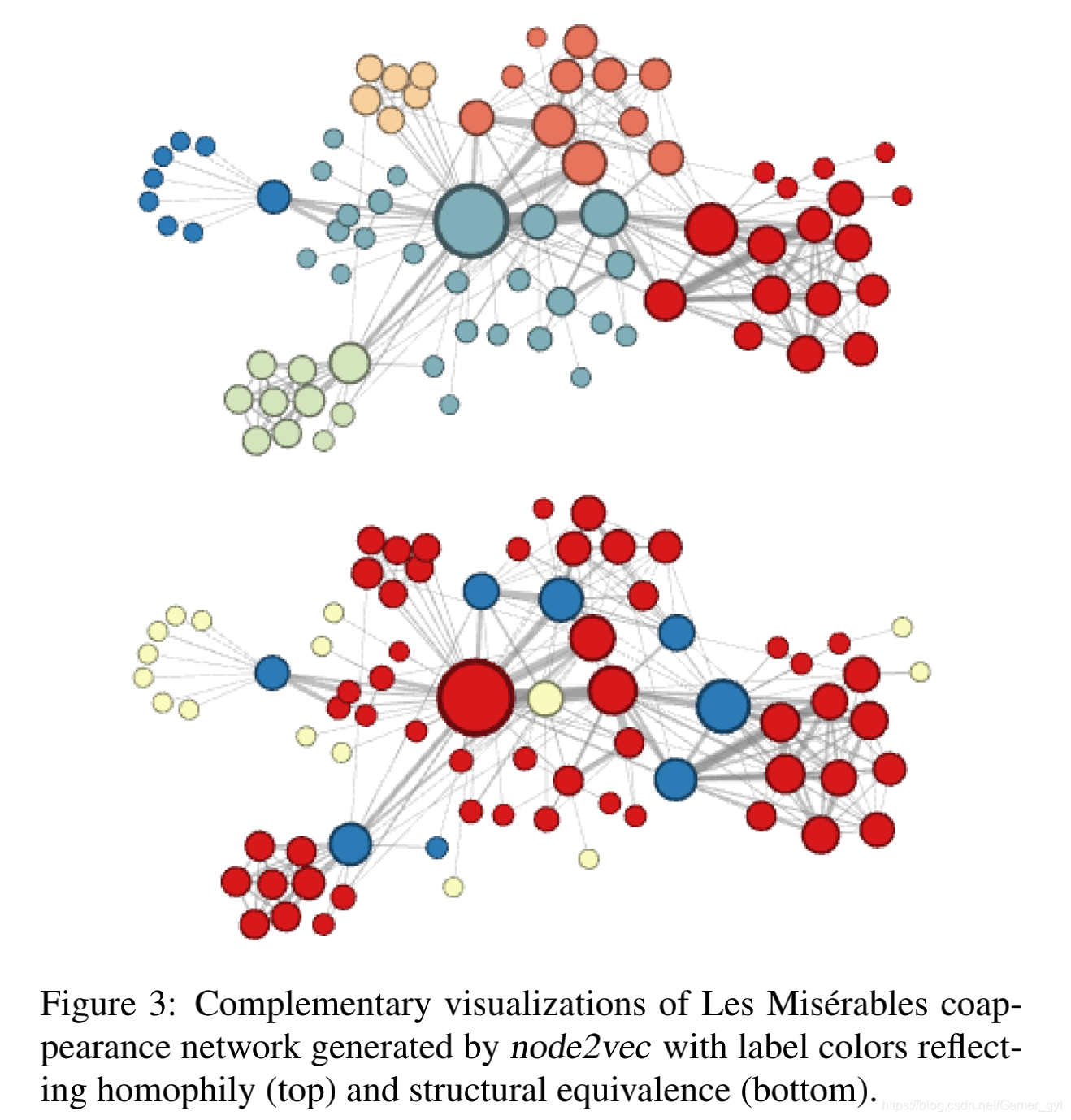
图的上半部分是倾向于 DFS（p=1，q=0.5）的，可以看到，这种方式得到的 embedding 似乎有很好的聚类性质，注意这里要看结点之间的连接而不是在 2D 平面上的距离，每个簇的边界结点跟内部的联系要比跟外部的联系更多一些。作者认为这反映了网络的同质性。

图的下半部分是倾向于 BFS（p=1，q=2.0），一个很明显的不同就是，这种方式得到的 embedding 似乎是按功能划分的，处于 graph 边缘的结点（黄色）有类似的 embedding，连接 graph 边缘和中心的结点（蓝色，在上半部分中作为簇边界的结点）有类似的 embedding，这些结点并不都是互相连接的，但是 node2vec 得到的 embedding 仍然能学习出这样的信息。作者认为这反映了网络的结构性。

3.2 Multi-label classifification

论文中将node2vec和Deepwalk、Line、Spectral Clustering进行了对比，在数据集BlogCatalog、Protein-Protein Interactions、Wikipedia进行了充分实验，继而证明了node2vec的优势！

数据集下载地址：

• BlogCatalog：http://networkrepository.com/soc-BlogCatalog.php
• Protein-Protein Interactions：https://info.sciex.com/native-mode-analysis
• Wikipedia：https://www.wikidata.org/wiki/Wikidata:Database_download/zh

关于实验参数：

LINE、Deepwalk、Node2vec共用参数：

• $d$ = 128
• $\gamma$ = 10
• $l$= 80
• $k$ = 10

关于Node2vec中 $p、q$ 参数使用网格搜索：{0.25, 0.50, 1, 2, 4}

实验评估指标：Macro-F1 and Micro-F1 （两个指标的含义可以参考：论文｜DeepWalk的算法原理、代码实现和应用说明）

实验结果：吧啦吧啦贼好！

4 代码实现

node2vec的实现其实并不复杂，大家可以自己尝试实现，这里推荐两个实现集成：

• 一个是阿里浅梦大佬实现的一个库，对应的git地址是：https://github.com/shenweichen/GraphEmbedding，其中还包含了其他一些embedding算法的代码实现
• 一个是清华大学NLP升级的网络嵌入工具包：OpenNE，关于OpenNE的介绍可以参考：https://nlp.csai.tsinghua.edu.cn/news/openne-pytorch/，对应的git代码库为：https://github.com/thunlp/OpenNE

5 应用

5.1 node2vec 同质性和结构性再思考

再看上面「实验说明-Case研究部分」的图，再思考一下同质性和结构性的含义，就会发现和直觉上的含义不同了。同质性并不是一个微观上的性质，作者说的同质性是能模型能找出每个簇的边界，使得簇内结点彼此联系的紧密程度要超过跟簇外结点的联系，这就要求模型有更大的感受野，DFS 这种能跳出局部的方式就很适合这个要求。

结构性就比较让人疑惑了，Figure 3 给出的关于结构性的表达似乎和我们直觉上差异不大，有着类似连接方式的结点会更相似。但是，BFS 竟然能做到这一点？那些 embedding 相似的结点甚至并不相互连接，BFS 为什么能有这种效果呢？

这里先给出后面做完实验后，感觉比较合适的一个解释。作者说的结构性并不是宏观上有相似的连接方式，而是指能够充分学习微观上的局部结构。比方说结点处于一个三角形连接的内部（很多论文会称之为 motif），BFS 会加强对这个三角形的感知，而 DFS 则容易通过连向外界的边跳出去，所以 BFS 对局部结构得学习会比 DFS 好，这也符合对 Figure 3 的观察。但是，这并不能解释 Figure 3 中按功能划分结点这个现象，我的结论是：这种现象只能在合适的数据上，在合适的超参设定下被观察到。

更多更完整的内容可以看：详解图表示学习经典算法 node2vec

5.2 node2vec 应用-微信朋友圈广告Lookalike问题

可以参考：当机器学习遇上复杂网络：解析微信朋友圈 Lookalike 算法

上面的这篇文章比较老了，但是应用node2vec去解决实际的问题这种思路还是比较值得借鉴的，原文太长，下面对其做个简单的总结。

文章中主要是用node2vec解决微信朋友圈广告lookalike问题，这种问题一般有两种做法：

• 第一种就是显性的定位，广告主根据用户的标签直接定位，比如说通过年龄、性别、地域这样的标签来直接圈定一部分用户进行投放
• 第二种做法，通过一个机器学习的模型，来定位广告主的潜在用户

广告主可以通过广告提交页面提交自己的广告需求，后台会给广告主圈定一部分潜在用户，这个就是我们称为Lookalike的模块。

那么如何利用node2vec算法来解决呢？首先基于微信好友之间的关键构建graph，然后可以控制 $p、q$ 参数生成 user embedding，然后可以根据已知用户进行相似用户筛选，继而圈定一批广告投放用户。

那么lookalike问题是如何结合node2vec中的同质性和结构性的？本质原因是社交关系数据有两个核心价值，即社交同质性和社交影响力，这是网络科学研究界的学者给出来的比较严谨的定义。其直观表现是：用户点击广告的概率会随着互动好友数量的增多而增长。

同质性说得更容易理解一点，就是相似性，我们跟好友可能会有兴趣的相似，或者我们同一个行业我们有行业背景的相似，我们才会形成好友。比如拿广告投放来说，广告主给了我客户名单即种子用户，是不是我种子用户的好友也会喜欢这个广告？

另一个维度就是影响力，影响力说的是我的行为会受到好友的影响。那这个点投放到朋友圈广告上，我可以看到朋友对广告的反馈，会受到他的影响。

所以说做朋友圈广告，我们重点会挖掘这两个价值，就是社交同质性和社交影响力。而这也和node2vec中的同质性和结构性不谋而合！

当然node2vec本质上也是一个graph，我们可以基于用户或者item构建这样的graph，然后生成user侧或者item侧的embedding，继而进行i2i或者u2u2i相关的召回，当然也可以直接吧embedding作为user侧、item侧的特征在粗排模型、精排模型进行使用。

---

【技术服务】详情点击查看： https://mp.weixin.qq.com/s/PtX9ukKRBmazAWARprGIAg

---

扫一扫关注「搜索与推荐Wiki」！号主「专注于搜索和推荐系统，以系列分享为主，持续打造精品内容！」