SDNE（Structural Deep Network Embedding）是一种用于图嵌入的深度学习算法，旨在捕捉图中的一阶和二阶相似度。该算法通过结合无监督的深度自编码器和有监督的拉普拉斯特征映射，同时考虑了节点的相邻关系和邻居集的相似性。模型优化目标包含一阶和二阶相似度损失函数，并引入正则项防止过拟合。实验部分在多个数据集上对比了SDNE与其他模型，如Deepwalk、LINE等，证明了SDNE在节点分类任务上的优越性能。此外，SDNE在电商场景中的应用，如凑单推荐，通过构建商品网络并进行有监督的embedding，有效挖掘商品间的潜在关联，提升推荐系统的准确性。
1.概述
SDNE（Structural Deep Network Embedding）算法是发表在KDD-2016上的一篇文章，论文的下载地址为：https://www.kdd.org/kdd2016/papers/files/rfp0191-wangAemb.pdf
SDNE主要也是用来构建node embedding的，和之前介绍的node2vec发表在同年，但不过node2vec可以看作是deepwalk的扩展，而SDNE可以看作是LINE的扩展。
2.算法原理
SDNE和LINE中相似度的定义是一致的，同样是定义了一阶相似度和二阶相似度，一阶相似度衡量的是相邻的两个顶点对之间相似性，二阶相似度衡量的是，两个顶点他们的邻居集合的相似程度。
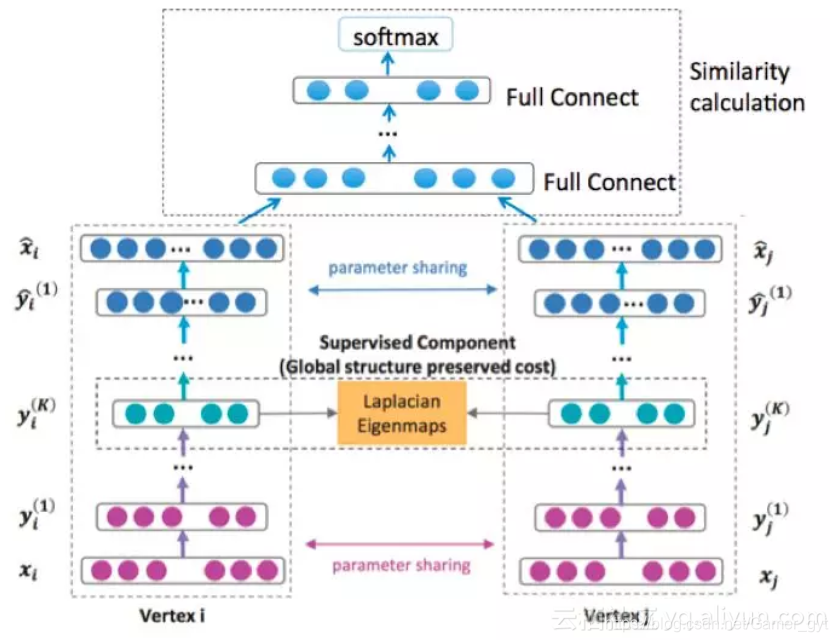
模型结构 如下：
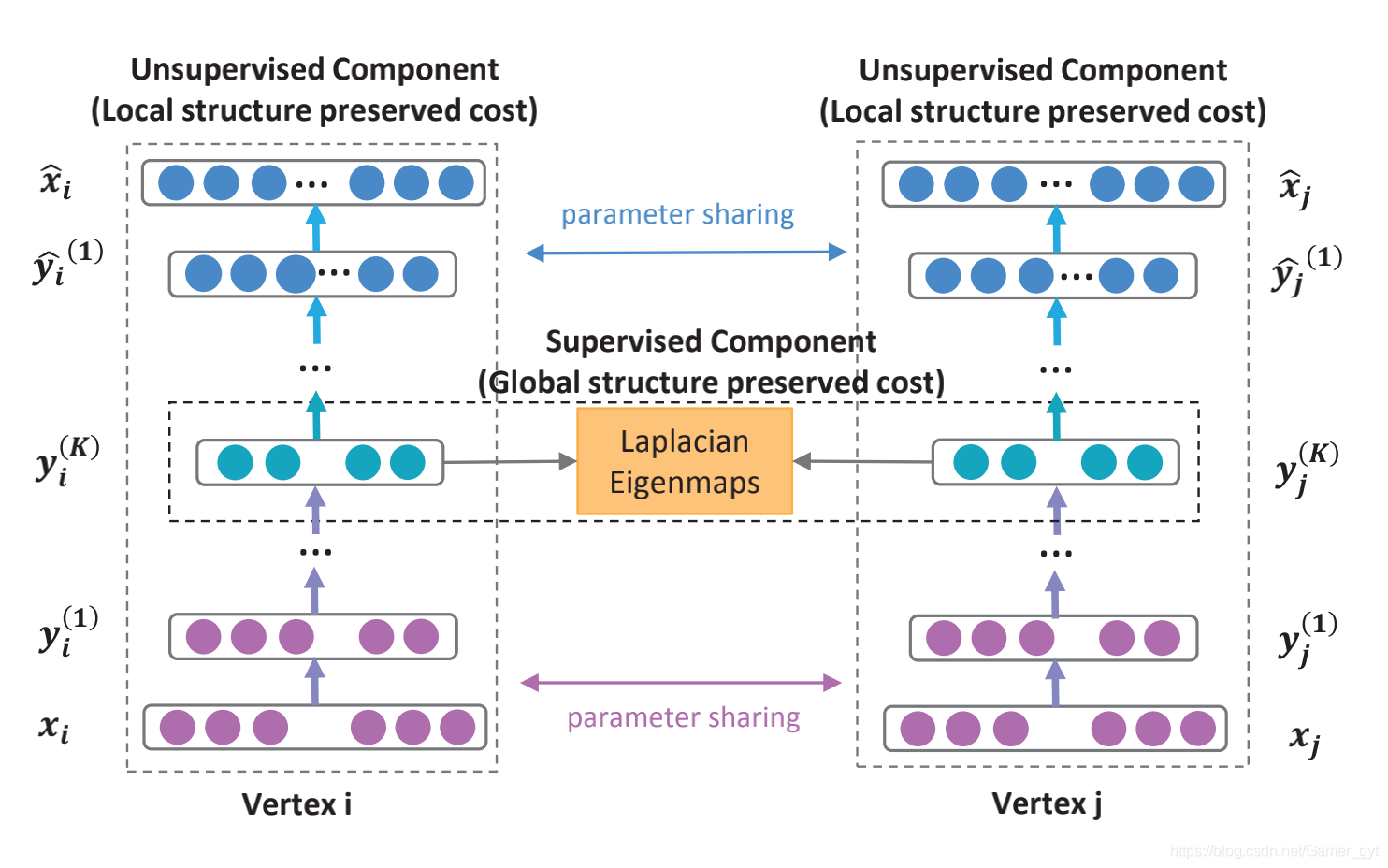
模型主要包括两个部分：无监督和有监督部分，其中：
- 无监督部分是一个深度自编码器用来学习二阶相似度（上图中两侧部分）
- 监督部分是一个拉普拉斯特征映射捕获一阶相似度（中间的橘黄色部分）
对于一阶相似度，损失函数定义如下：
L
1
s
t
=
∑
i
,
j
=
1
s
i
,
j
∥
y
i
K
−
y
j
K
∥
2
2
=
∑
i
,
j
=
1
s
i
,
j
∥
y
i
−
y
j
∥
2
2
L_{1st}=\sum_{i,j=1}s_{i,j} \left \| y_i^K - y_j^K \right \| _{2}^{2} = \sum_{i,j=1}s_{i,j} \left \| y_i - y_j \right \| _{2}^{2}
L1st=i,j=1∑si,j∥∥yiK−yjK∥∥22=i,j=1∑si,j∥yi−yj∥22
该损失函数可以让图中的相邻的两个顶点对应的embedding vector在隐藏空间接近。
论文中还提到一阶相似度的损失函数还可以表示为：
L
1
s
t
=
∑
i
,
j
=
1
s
i
,
j
∥
y
i
−
y
j
∥
2
2
=
2
t
r
(
Y
T
L
Y
)
L_{1st}=\sum_{i,j=1}s_{i,j} \left \| y_i - y_j \right \| _{2}^{2} = 2tr(Y^TLY)
L1st=i,j=1∑si,j∥yi−yj∥22=2tr(YTLY)
其中：
- L L L 是图对应的拉普拉斯矩阵
- L = D − S L = D - S L=D−S， D D D 是图中顶点对应的度矩阵， S S S 是邻接矩阵， D i , i = ∑ j s i , j D_{i,i} = \sum_{j}s_{i,j} Di,i=∑jsi,j
拉普拉斯矩阵是「图论」中重要的知识点，可以参考：https://blog.youkuaiyun.com/qq_30159015/article/details/83271065，查看更清晰的介绍
对于二阶相似度，损失函数定义如下：
L
2
n
d
=
∑
i
n
∥
x
i
^
−
x
i
∥
2
2
L_{2nd} = \sum_{i}^{n} \left \| \hat{x_i} - x_i \right \| _{2}^{2}
L2nd=i∑n∥xi^−xi∥22
这里使用图的邻接矩阵进行输入，对于第
i
i
i 个顶点，有
x
i
=
s
i
x_i = s_i
xi=si ，每一个
s
i
s_i
si 都包含了顶点
i
i
i 的邻居结构信息，所以这样的重构过程能够使得结构相似的顶点具有相似的embedding表示向量。
但是现实中由于图都是稀疏的，邻接矩阵
S
S
S 中的非零元素是远远少于零元素的，那么对于神经网络来说只要全部输出0也能取得一个不错的效果，这不是我们想要的。为了解决这个问题，论文提出一种使用带权损失函数，对于非零元素具有更高的惩罚系数。 修正后的损失函数为：
L
2
n
d
=
∑
i
n
∥
(
x
i
^
−
x
i
)
⊙
b
i
∥
2
2
=
∥
(
X
i
^
−
X
i
)
⊙
B
∥
F
2
L_{2nd} = \sum_{i}^{n} \left \| (\hat{x_i} - x_i) \odot b_i \right \| _{2}^{2} = \left \| (\hat{X_i} - X_i) \odot B \right \| _{F}^{2}
L2nd=i∑n∥(xi^−xi)⊙bi∥22=∥∥∥(Xi^−Xi)⊙B∥∥∥F2
其中：
- ⊙ \odot ⊙ 为逐元素积
- b i = { b i , j } j = 1 n b_i = \left \{ b_{i,j} \right \}_{j=1}^{n} bi={bi,j}j=1n，若 s i , j = 0 s_{i,j}=0 si,j=0，则 b i , j = 1 b_{i,j}=1 bi,j=1，否则 b i , j = β > 1 b_{i,j} = \beta >1 bi,j=β>1
模型整体的优化目标为：
L
m
i
x
=
α
L
1
s
t
+
L
2
n
d
+
v
L
r
e
g
L_{mix} = \alpha L_{1st} + L_{2nd} + v L_{reg}
Lmix=αL1st+L2nd+vLreg
其中：
- L r e g L_{reg} Lreg 为正则项， α \alpha α 为控制一阶损失的参数， v v v 为控制正则化项的参数
3.实验
实验部分主要就是为了验证SDNE的效果要比其他的模型好，因此作者在5个数据集中进行了实验，分别为：
- BLOGCATALOG
- FLICKR
- YOUTUBE
- ARXIV GR-QC
- 20-NEWSGROUP
这里选取的对比模型包括：
- Deepwalk
- LINE
- GraRep
- Laplacian Eigenmaps (LE)
- Common Neighbor
实验评估的指标为：
- precision@k：top k的精确度
- Mean Average Precision (MAP)：平均误差
- Macro-F1：区分类别的F1-Score
- Micro-F1 ：不区分类别的F1-Score
Macro-F1和Micro-F1区别参考：https://zhuanlan.zhihu.com/p/64315175
4.代码实现
代码实现部分可以参考：https://github.com/xiaohan2012/sdne-keras
其中关于SDNE模型的定义部分为：
class SDNE():
def __init__(self,
graph,
encode_dim,
weight='weight',
encoding_layer_dims=[],
beta=2, alpha=2,
l2_param=0.01):
"""graph: nx.Graph
encode_dim: int, length of inner most dim
beta: beta parameter under Equation 3
alpha: weight of loss function on self.edges
"""
self.encode_dim = encode_dim
###################
# GRAPH STUFF
###################
self.graph = graph
self.N = graph.number_of_nodes()
self.adj_mat = nx.adjacency_matrix(self.graph).toarray()
self.edges = np.array(list(self.graph.edges_iter()))
# weights
# default to 1
weights = [graph[u][v].get(weight, 1.0)
for u, v in self.graph.edges_iter()]
self.weights = np.array(weights, dtype=np.float32)[:, None]
if len(self.weights) == self.weights.sum():
print('the graph is unweighted')
####################
# INPUT
####################
# one end of an edge
input_a = Input(shape=(1,), name='input-a', dtype='int32')
# the other end of an edge
input_b = Input(shape=(1,), name='input-b', dtype='int32')
edge_weight = Input(shape=(1,), name='edge_weight', dtype='float32')
####################
# network architecture
####################
encoding_layers = []
decoding_layers = []
embedding_layer = Embedding(output_dim=self.N, input_dim=self.N,
trainable=False, input_length=1, name='nbr-table')
# if you don't do this, the next step won't work
embedding_layer.build((None,))
embedding_layer.set_weights([self.adj_mat])
encoding_layers.append(embedding_layer)
encoding_layers.append(Reshape((self.N,)))
# encoding
encoding_layer_dims = [encode_dim]
for i, dim in enumerate(encoding_layer_dims):
layer = Dense(dim, activation='sigmoid',
kernel_regularizer=regularizers.l2(l2_param),
name='encoding-layer-{}'.format(i))
encoding_layers.append(layer)
# decoding
decoding_layer_dims = encoding_layer_dims[::-1][1:] + [self.N]
for i, dim in enumerate(decoding_layer_dims):
if i == len(decoding_layer_dims) - 1:
activation = 'sigmoid'
else:
# activation = 'relu'
activation = 'sigmoid'
layer = Dense(
dim, activation=activation,
kernel_regularizer=regularizers.l2(l2_param),
name='decoding-layer-{}'.format(i))
decoding_layers.append(layer)
all_layers = encoding_layers + decoding_layers
####################
# VARIABLES
####################
encoded_a = reduce(lambda arg, f: f(arg), encoding_layers, input_a)
encoded_b = reduce(lambda arg, f: f(arg), encoding_layers, input_b)
decoded_a = reduce(lambda arg, f: f(arg), all_layers, input_a)
decoded_b = reduce(lambda arg, f: f(arg), all_layers, input_b)
embedding_diff = Subtract()([encoded_a, encoded_b])
# add weight to diff
embedding_diff = Lambda(lambda x: x * edge_weight)(embedding_diff)
####################
# MODEL
####################
self.model = Model([input_a, input_b, edge_weight],
[decoded_a, decoded_b, embedding_diff])
reconstruction_loss = build_reconstruction_loss(beta)
self.model.compile(optimizer='adadelta',
loss=[reconstruction_loss, reconstruction_loss, edge_wise_loss],
loss_weights=[1, 1, alpha])
self.encoder = Model(input_a, encoded_a)
# for pre-training
self.decoder = Model(input_a, decoded_a)
self.decoder.compile(optimizer='adadelta',
loss=reconstruction_loss)
def pretrain(self, **kwargs):
"""pre-train the autoencoder without edges"""
nodes = np.arange(self.graph.number_of_nodes())
node_neighbors = self.adj_mat[nodes]
self.decoder.fit(nodes[:, None],
node_neighbors,
shuffle=True,
**kwargs)
def train_data_generator(self, batch_size=32):
# this can become quadratic if using dense
m = self.graph.number_of_edges()
while True:
for i in range(math.ceil(m / batch_size)):
sel = slice(i*batch_size, (i+1)*batch_size)
nodes_a = self.edges[sel, 0][:, None]
nodes_b = self.edges[sel, 1][:, None]
weights = self.weights[sel]
neighbors_a = self.adj_mat[nodes_a.flatten()]
neighbors_b = self.adj_mat[nodes_b.flatten()]
# requires to have the same shape as embedding_diff
dummy_output = np.zeros((nodes_a.shape[0], self.encode_dim))
yield ([nodes_a, nodes_b, weights],
[neighbors_a, neighbors_b, dummy_output])
def fit(self, log=False, **kwargs):
"""kwargs: keyword arguments passed to `model.fit`"""
if log:
callbacks = [keras.callbacks.TensorBoard(
log_dir='./log', histogram_freq=0,
write_graph=True, write_images=False)]
else:
callbacks = []
callbacks += kwargs.get('callbacks', [])
if 'callbacks' in kwargs:
del kwargs['callbacks']
if 'batch_size' in kwargs:
batch_size = kwargs['batch_size']
del kwargs['batch_size']
gen = self.train_data_generator(batch_size=batch_size)
else:
gen = self.train_data_generator()
self.model.fit_generator(
gen,
shuffle=True,
callbacks=callbacks,
pickle_safe=True,
**kwargs)
def get_node_embedding(self):
"""return the node embeddings as 2D array, #nodes x dimension"""
nodes = np.array(self.graph.nodes())[:, None]
return self.encoder.predict(nodes)
def save(self, path):
self.model.save(path)
5.应用
以下内容来自：https://developer.aliyun.com/article/419706
SDNE算法主要应用是电商场景的「凑单」，比如在618、双十一这样的场景中会有满200-30这样的场景，当用户加购的商品不足200时，会进行提示凑单。
其主要流程为：
-
基于用户购买行为构建graph，节点：商品，边：商品间同时购买的行为，权重：同时购买的比重，可以是购买次数、购买时间、金额等feature
-
基于权重Sampling（weighted walk）作为正样本的候选，负样本从用户非购买行为中随机抽样
-
embedding部分将无监督模型升级成有监督模型，将基于weighted walk采出来的序，构造成item-item的pair对，送给有监督模型（DNN）训练
-
依据产出的embedding，计算item之间的相似度，生成item 的相似 item list
5.1 算法流程
整体算法的架构图为：
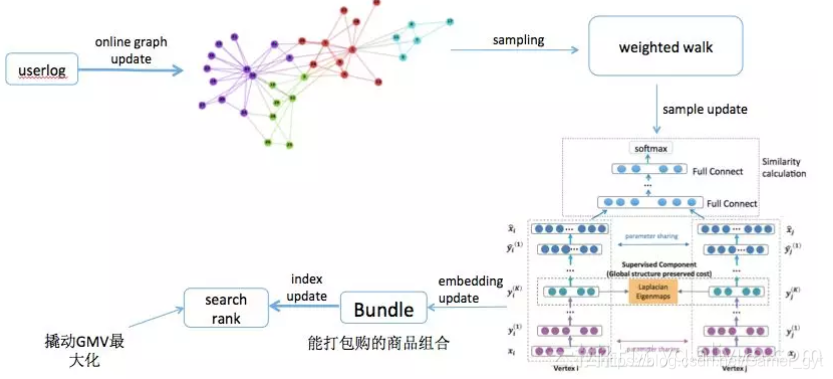
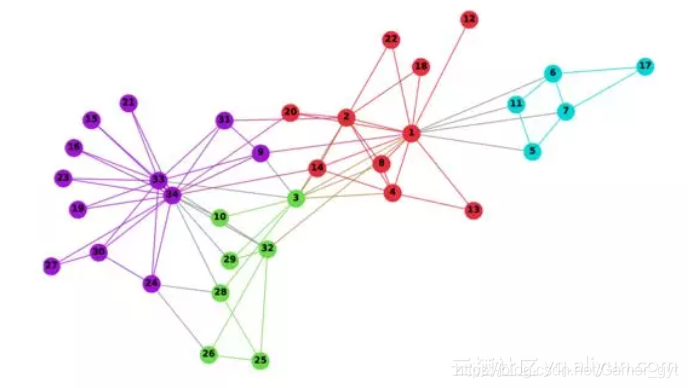
5.1.1 构建Graph
上文提到，我们要挖掘商品间共同购买的关系（bundle mining），类似买了又买的问题，所以，我们构建的graph是带权重的商品网络，节点：商品，边：商品间共同购买的关系，权重：共同购买次数、购买时间。
5.1.2 Sampling
传统的方法，比如deep walk，它的Sampling本质上是有两部分，首先，通过random walk的方式进行游走截断，其次，在仍给word2vec中Skip-Gram模型进行embedding之前，用negative sampling的方式去构造样本；这种随机采样的方法会大概率的将热门节点采集为负样本，这种方式适用于语言模型，因为在自然语言中，热门的单词均为无用单词（比如he、she、it、is、the）。对于我们的商品网络，刚好相反，热门商品往往是最重要的样本，如果采用negative sampling的方式去构造样本，模型肯定是学不出来。因此，我们基于边的权重去采样（weighted walk），使采样尽量往热门节点方向游走，以下图为例：
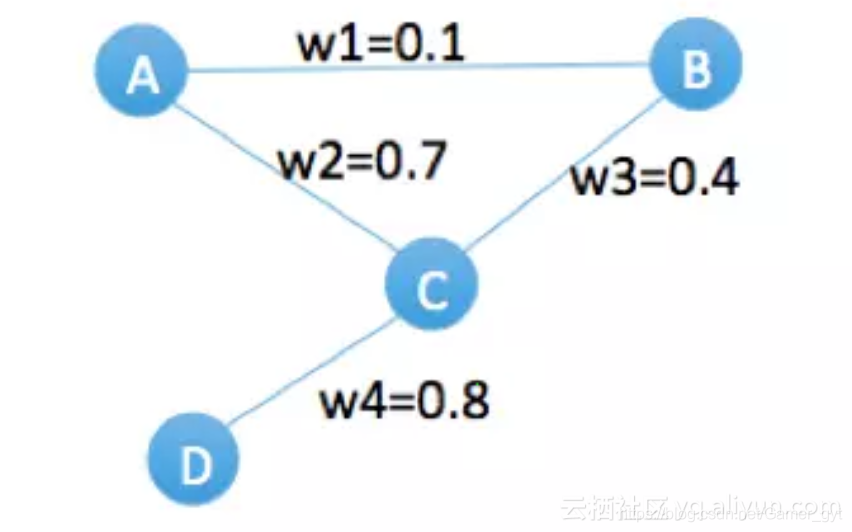
举个例子来说，假设游走2步，从节点A出发，随机取下一个邻居节点时，如果是random walk算法，它会等概率的游走到B或C节点，但是我们的算法会以7/8的概率取节点C，再会以8/12的概率游走到节点D，最终很大概率上会采出来一条序walk=（A，C，D），对于原始graph，A和D是没有关联的，但是通过weighted walk，能够有效的挖掘出A和D的关系，算法详见：
5.1.3 Embedding
上一部分介绍了如何构建了带权重的概率图，基于带权重的采样（weighted walk）作为正样本的候选，负样本从用户非购买行为中随机抽样；这一部分主要介绍embedding的部分，将基于weighted walk采出来的序，构造成item-item的pair对，送给embedding模型，我们构造了一个有监督embedding模型（DNN），规避无监督模型无法离线评估模型效果的问题。模型结构如下图。
5.2 实现
5.2.1 离线
a）训练：离线模型在PAI平台上用tensorflow框架实现，抽取了历史50天的全网成交数据，大概抽取3000万节点，构建的graph，在odps graph平台做完weighted walk，产出2亿条样本，也就是item-item的pair对，训练至收敛需要2小时的时间
b）预测：从全网所有行为中，随机抽取几十亿条pair对，去做预测，给每对item pair预测一个score
c）上线：对每个种子商品取topN的bundle商品，打到搜索引擎的倒排和正排字段，从qp中取出每个用户的种子商品，基于倒排字段召回bundle商品，基于正排字段做bundle排序
5.2.2 实时
用户购买行为，日常和大促差异很大，为了能够实时的捕获用户实时行为，我们在porsche上建了一套实时计算bundle mining的流程：
a）数据预处理：在porsche上对用户实时日志进行收集，按离线的数据格式处理成实时的数据流
b）Sampling：发送给odps graph实时计算平台，构建graph，做weighted walk，生成序，再通过swift消息发出
c）Embedding：在porsche上做DNN模型训练和实时预测
d）数据后处理：计算item的topN的bundle item list，实时写到dump和引擎
扫一扫关注「搜索与推荐Wiki」！号主「专注于搜索和推荐系统，以系列分享为主，持续打造精品内容！」
扫一扫
612
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
