216. Combination Sum III
Tag BackTracking
Difficulty Medium
Link https://leetcode-cn.com/problems/combination-sum-iii/
思路
这道题和前面的两道组合数之和类似,只不过增加了对每条路径的元素数量的限制
candidates限定为[1,2,3,4,5,6,7,8,9]
仿照前面的模板,可以很轻易的写出如下代码
class Solution {
public List<List<Integer>> combinationSum3(int k, int n) {
List<List<Integer>> res = new ArrayList<>();
if (k <= 0 || n <= 0 || n > 55) {
return res;
}
Deque<Integer> path = new ArrayDeque<>();
int[] candidates = {1, 2, 3, 4, 5, 6, 7, 8, 9};
dfs(candidates, k, n, 0, path, res);
return res;
}
public void dfs(int[] candidates, int k, int n, int begin, Deque<Integer> path, List<List<Integer>> res) {
// 基准条件
if (k == 0 && n == 0) {
res.add(new ArrayList<>(path));
return;
}
if (k == 0 || n == 0) {
return;
}
for (int i = begin; i < candidates.length; i++) {
path.add(candidates[i]);
dfs(candidates, k - 1, n - candidates[i], i + 1, path, res);
path.removeLast();
}
}
}
当然,还可以通过剪枝对其进行优化,我们通过画图可以更加直观的看出来。
假设k=3,n=7
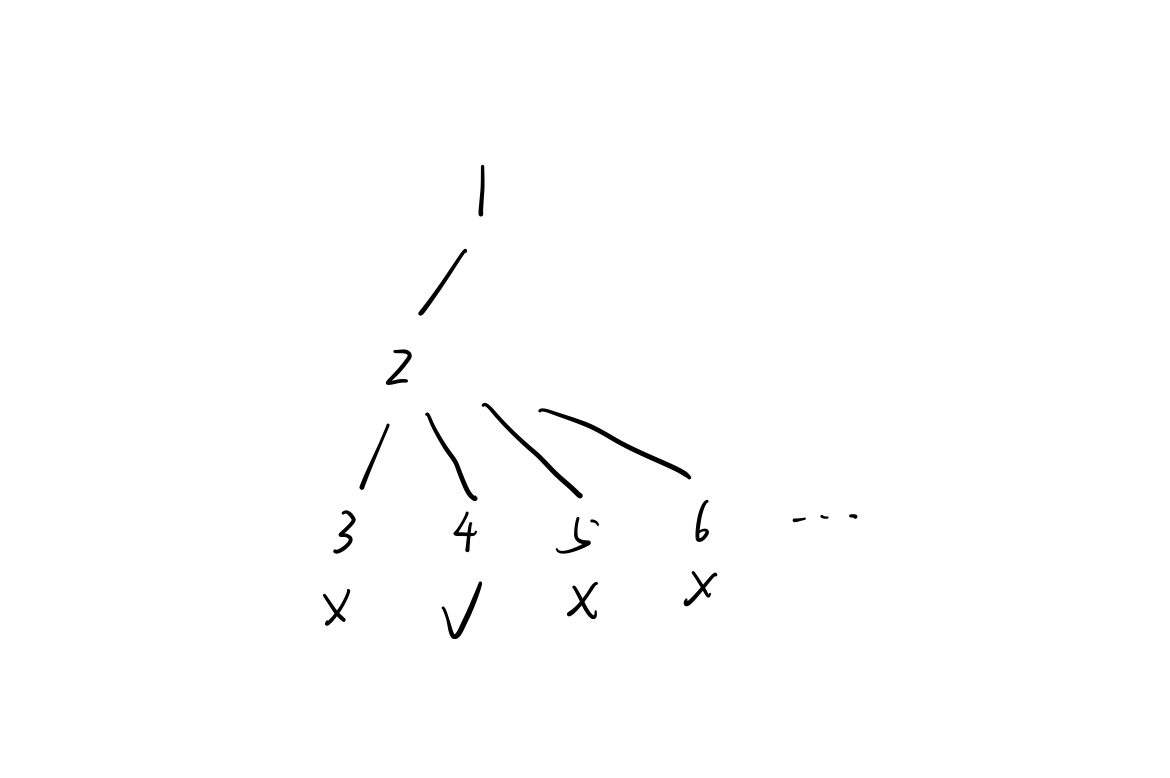
可以看到,在得到[1,2,4]这个正确组合后,程序还去判断了后续的[1,2,5],[1,2,6]等,这就造成了浪费。使用如下注释的地方的剪枝,可以超过100%的用户。
class Solution {
public List<List<Integer>> combinationSum3(int k, int n) {
List<List<Integer>> res = new ArrayList<>();
if (k <= 0 || n <= 0 || n > 55) {
return res;
}
Deque<Integer> path = new ArrayDeque<>();
int[] candidates = {1, 2, 3, 4, 5, 6, 7, 8, 9};
dfs(candidates, k, n, 0, path, res);
return res;
}
public void dfs(int[] candidates, int k, int n, int begin, Deque<Integer> path, List<List<Integer>> res) {
if (k == 0 && n == 0) {
res.add(new ArrayList<>(path));
return;
}
for (int i = begin; i < candidates.length; i++) {
// 如果路径和还未达到n,则去后面寻找更大的数
if (k == 1 && n - candidates[i] > 0) {
continue;
}
// 大剪枝:如果路径和已经超过k,那么直接退出这条路径
if (k == 1 && n - candidates[i] < 0) {
break;
}
path.add(candidates[i]);
dfs(candidates, k - 1, n - candidates[i], i + 1, path, res);
path.removeLast();
}
}
}
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








