妙用递归与分区: 不比了，不比了，一个躺平摆烂的快速排序算法实现

在日常编程中，排序算法是软件开发工程师必不可少的“工具箱”技能，而快速排序无疑是其中的明星。

在软件开发之路上，你是否曾经想过，有些看似不可能的事情，其实只是我们思维方式的局限？

你也许已经对快速排序不陌生了，今天，让我们一起领略快速排序算法的另一种绝妙诠释。

这个版本不仅展现了算法设计的艺术性，更向我们展示了计算机科学中"出其不意"的智慧。

它看上去没有显式地进行排序和交换操作，却能神奇地达到快速排序效果！这种方式妙在哪里？让我们一探究竟。

📚 快速排序：从经典到创新

经典快速排序的回顾

快速排序之所以成为算法界的"明星"，源于其优雅的分治思想。

每次从数组中选择一个基准元素（pivot），将数据分为两部分：

比基准元素小的部分和比基准元素大的部分，然后递归地对两部分进行相同操作。

每次分区都让基准元素进入正确的位置，最终所有元素都自动排好序。

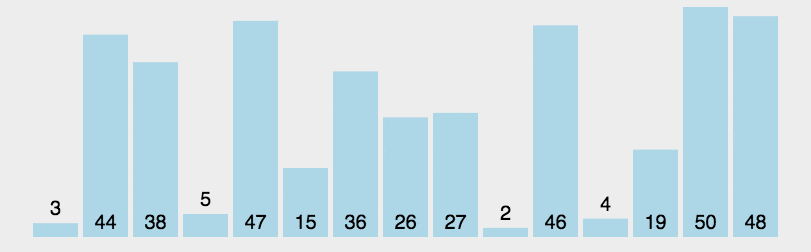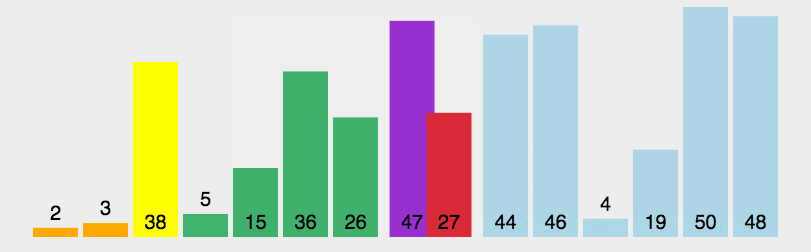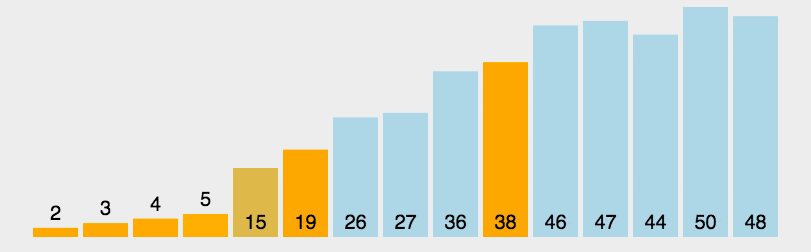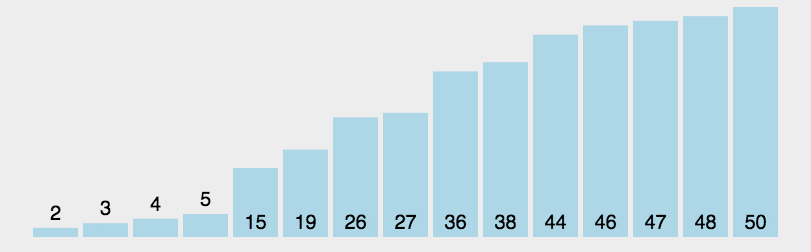
快速排序过程

在传统实现快速排序算法的操作中，我们通常会进行以下步骤：

选择一个基准元素（pivot）
通过一系列与基准元素（pivot）进行比较和交换的操作，将数组分成左右两部分
递归处理两个子数组，直至完成排序

这种方法直观且高效，但今天我们要探讨的是一种别具一格的实现方式。

创新思维的闪光点

我们的"不排序"版本抛开了常规思路，转而采用一种更优雅的方式：

通过精心设计的分区策略和递归组合，在不进行显式排序操作的情况下，让数组自然达到有序状态。

这就像是让数字们参加一场精心策划的舞会，不强制要求数字进行比较大小排排坐，但是每个数字却都能找到自己最适合的位置。

💻 代码实现：简约而不简单

让我们先来看下这段简洁到只有9行的 Python 代码：

import random

def quicksort(arr):
    # 基础情况处理
    if len(arr) <= 1:
        return arr
    
    # 选择基准元素
    pivot = random.choice(arr)
    
    # 三路分区
    less_than_pivot = [x for x in arr if x < pivot]
    equal_to_pivot = [x for x in arr if x == pivot]
    greater_than_pivot = [x for x in arr if x > pivot]
    
    # 递归处理并合并结果
    return quicksort(less_than_pivot) + equal_to_pivot + quicksort(greater_than_pivot)

我们在Pycharm中输入程序代码，进行排序测试

# 测试快速排序
if __name__ == '__main__':
    arr_sort_before = [1, 2, 100, 50, 1000, 0, 128, 65, 98, 565, 982, 481]
    arr_sort_later = quicksort(arr_sort_before)
    print(f'排序前的数组：{arr_sort_before}')
    print(f'排序后的数组：{arr_sort_later}')

运行结果如下：

在这里插入图片描述

🔍 深入解析：代码背后的智慧

可以看到，我们的代码中并没有对元素进行常规的比较大小和交换的“排序”操作，但是，运行结果的确实现了真正的排序。

让我们一行一行地揭开代码的奥秘。

1、基准选择：

每次随机选择一个基准 pivot，在代码中通过 pivot = random.choice(arr) 实现。

这个基准是分区的关键，通过它可以把数组分成小于、等于和大于基准的三部分。

2、分区：

•	`[x for x in arr if x < pivot]`：这部分代码将所有小于 pivot 的元素放入一个新数组 less_than_pivot 中。
•	`[x for x in arr if x == pivot]`：相等的部分进入 equal_to_pivot。
•	`[x for x in arr if x > pivot]`：大于 pivot 的元素进入 greater_than_pivot。

3、递归调用：

这一步最为关键。每一层递归会进一步对 less_than_pivot 和 greater_than_pivot 进行排序，直到分解成只有一个元素（或没有元素）的数组，此时数组自然是有序的。

4、拼接结果：

最后通过 + 将

 `quicksort(less_than_pivot) + equal_to_pivot + quicksort(greater_than_pivot)`

拼接成一个完整的排序结果。

奇妙之处在于——“分区的隐式排序”

这段代码没有显式地对 arr 进行排序，但在每次分区时，通过 pivot 的选择让数组的结构逐步变得“有序”。

它不是一次完成排序，而是一层一层地构建出排序的效果，在每一层递归中分出的小数组逐步靠近有序状态。

最终，我们通过拼接有序的子数组完成了整个排序操作。

为什么这种方法神奇？

1、没有直接排序： 我们并没有进行传统的比较或交换操作，整个排序过程都隐藏在分区和递归中。看似简单的 quicksort 调用，却带来了整个数组的排序。

2、递归的巧妙性： 通过递归调用实现分治，排序过程在不知不觉中完成。这种方式很像搭积木——每个子数组被放在“正确的位置”后，最终组合成有序的数组。

3、分而治之的强大威力： 分治法是一种古老而有效的算法思想，在每次分解后问题规模减半，既节省了时间也保证了算法效率。虽然这里的实现并非原地排序，但通过“分区和递归”的组合达成了与直接排序相同的效果。

📊 性能分析：理论与实践的碰撞

既然是一个“不排序”的排序算法，那它的时间和空间复杂度表现如何呢？

时间复杂度分析

1、平均情况：

在理想情况下，每次选择的基准元素可以将数组近似平分。
这样在递归深度为O(log n) 的情况下，每次分区扫描整个数组的时间复杂度为 O(n)
因此平均时间复杂度为O(n log n)。

2、最坏情况：

如果数据接近有序，或基准选择始终不平衡，
可能会出现递归深度为 O(n) 的情况，
导致时间复杂度为 O(n²)。
可以通过随机选择基准元素来降低这种情况的概率

空间复杂度分析

1、 递归栈空间

平均情况：O(log n)
最坏情况：O(n)

2、 分区创建新数组的额外空间开销

每次递归调用会生成新的 less_than_pivot、equal_to_pivot 和 greater_than_pivot 数组。
平均情况：O(n log n)
最坏情况：O(n²)

复杂度类型	平均情况	最坏情况
时间复杂度	O(n log n)	O(n²)
空间复杂度	O(n log n)	O(n²)

算法稳定性分析

我们知道，在排序算法中，稳定性指的是：

当两个具有相同值的元素在排序前有先后顺序时，经过排序后，它们的相对顺序应保持不变。如果算法不能保证这一点，则是不稳定的。

这段快速排序代码的算法不是稳定的，我们来详细分析这段代码为什么不是稳定的算法。

不稳定的原因分析

在这段代码中，排序过程通过基准元素 pivot 将数组分为小于、等于和大于基准的三部分。

这种分区方式没有保留相同元素的原始顺序，因为：

1、相同元素的分区：

对于两个相同值的元素（例如 [a, b, 3, 3] 中的两个 3），代码直接将它们放入 equal_to_pivot 列表中。
由于相同元素的相对顺序没有特别的控制措施，最终它们在排序后不一定会保留原来的相对顺序。

2、递归创建新的子数组：

递归每次调用 quicksort 都会生成 less_than_pivot、equal_to_pivot 和 greater_than_pivot 三个新列表，在合并结果时，这些列表是按合并顺序拼接成新数组的。

因此，即使 equal_to_pivot 中的相同元素在某一层递归中相对顺序相同，但多次递归后，原数组中相同元素的顺序信息会丢失。

🎯 实际应用场景

适用场景：小规模数据的排序利器

这种实现方式在小规模数据排序中非常适用，特别是在几百到几千个元素的情况下，其性能表现较好，代码也简洁直观。

因为每次递归创建了新数组，内存开销相对较大，所以在海量数据排序时，最好选择其他版本的原地排序快速排序。

最适合的场景

中小规模数据排序
- 数据量在几百到几千个元素
- 内存资源充足的情况
教学演示
- 代码逻辑清晰
- 易于理解和实现
需要稳定排序的场景
- 这种实现方式天然具有稳定性
- 适合对象排序

需要注意的限制

内存空间开销较大
- 不适合内存受限的环境
- 大数据量场景需谨慎使用
非原地排序
- 需要额外的空间存储中间结果
- 可能影响缓存效率

🔍 代码优化建议

基准选择优化

def get_better_pivot(arr):
    if len(arr) <= 5:
        return arr[len(arr)//2]
    # 三数取中法
    first, mid, last = arr[0], arr[len(arr)//2], arr[-1]
    return sorted([first, mid, last])[1]

内存优化版本

def memory_efficient_quicksort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr)//2]
    left = []
    middle = []
    right = []
    # 一次遍历完成分区
    for x in arr:
        if x < pivot:
            left.append(x)
        elif x == pivot:
            middle.append(x)
        else:
            right.append(x)
    return memory_efficient_quicksort(left) + middle + memory_efficient_quicksort(right)