从一次面试说起
"下一位。"我抿了一口已经凉透的美式咖啡,继续翻开眼前的简历。
今天是我司后端开发工程师的面试日,作为技术委员会的资深面试官,我已经连续面试了8位候选人。
第9位候选人看起来颇具亮点:
6年互联网开发经验,负责过数个高并发系统,简历上写着"精通分布式架构设计"。似乎是一位很有潜力的候选人。
"你好,我是今天的面试官。"寒暄过后,我抛出了我最常用的第一道热身题:“能否写一个你最熟悉的排序算法?任意一种都可以。”
他露出了一丝自信的微笑:"这个简单。"随后在白板上迅速写下了选择排序的代码。
那一刻,我放下手中的咖啡杯,目光在代码和简历之间来回逡巡。15年的面试经验告诉我,这位看似经验丰富的候选人,可能比简历上的光鲜更值得深究。
为什么这样说?因为当一位声称精通分布式架构的工程师,在被问到最基础的算法题时,选择了O(n²)的选择排序算法,这背后往往隐藏着一些有趣的技术认知盲区…
记得去年,我们团队就遇到过一个典型案例:一位工程师在设计实时数据处理系统时,用选择排序处理用户标签。
结果在压测环节,面对每秒数十万条的实时数据流量,系统响应时间直线上升,最终导致了一次严重的线上事故…
看着白板上的选择排序代码,我不禁陷入沉思:这位候选人的技术栈是否如简历所述那般"精通"?他在设计高并发系统时,是否也是用这样的思维方式在处理性能问题?
这不仅仅是一个排序算法的选择问题,而是架构师在面对复杂系统时的思维方式、技术视野和工程素养的综合体现。
选择排序,这位算法界的“老前辈”,简单、直观,逻辑清晰,绝对算得上是早期计算机科学界的“清流”。
这个算法的设计源于人类最原始的思维方式,就像古代宫廷的侍从拾豆子:每次找到最小的一颗,整整齐齐摆在最前面,接着再找剩下的最小一颗,继续摆好,直到豆子按大小一字排开。
逻辑简单得令人发指!新手一看就懂,几分钟就能“上手”。
但为什么如今的工程应用中几乎见不到选择排序的身影了呢?
首先,选择排序的“出道”时期可是很早的,那时的计算机科学还处在发展的初期,算法的设计更注重简单和易实现。
选择排序的逻辑不仅简单而且便于手工操作,足够适应当时的计算需求,因此在早期教学和小型计算机上风光无限,甚至成为教学中讲解排序的经典案例。
随着计算机硬件和多核处理器的飞速发展,工程实践对算法提出了新的要求:不仅要快,还要“聪明”。
也就是说,要能够有效利用现代计算机的 CPU 缓存、预取机制和多核并行处理能力。
然而,这恰恰是选择排序的硬伤!
选择排序在处理大数据时需要频繁访问内存位置,访问模式不规则、不连续,极难向量化优化,且多核 CPU 也很难并行处理这一算法的步骤。
最终,选择排序因为难以高效利用现代硬件优势而逐渐淡出人们的视线。
进入 2000 年,选择排序的“寒冬”真正来临——Tim Peters 开发的 TimSort 横空出世。
这种算法结合了归并排序和插入排序的优势,尤其擅长处理真实世界中常见的混合排序需求。
TimSort 它不仅仅是算法的更新,更是对真实世界工程问题的深刻洞察,它能智能检测已排序区块并优化,这种对实际场景的思考,才是一个架构师应该具备的视野。
Python 和 Java 迅速将 TimSort 选为默认排序算法,选择排序在主流工程实践中被彻底“打入冷宫”。
所以,选择排序的“没落”虽充满传奇,却也不免让人唏嘘。
在现代软件工程中,这位经典算法早已失去了用武之地,静静躺在书本的某个角落,等待新手程序员偶尔的回顾和学习。
📊 选择排序算法的核心思想和实现
选择排序的核心思想是逐轮找到当前未排序部分的最小值,将其放到当前轮的起始位置,直至整个列表有序。
算法流程:
- 1、在未排序部分找到最小(或最大)元素。
- 2、将该元素放到已排序部分的末尾。
- 3、重复上述过程,直至所有元素排序完毕。
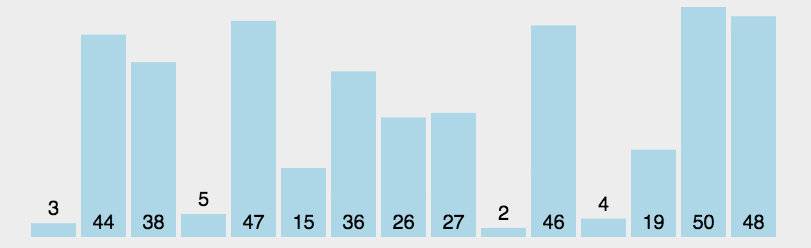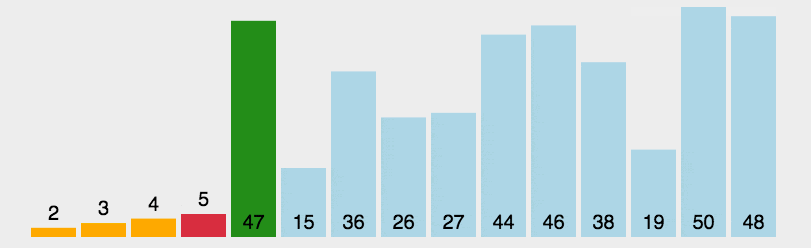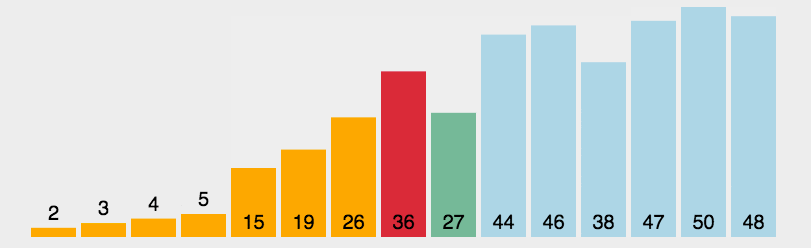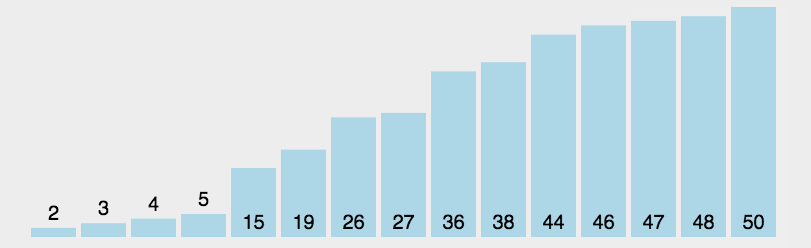
让我们看看选择排序的典型实现:
# 选择排序
def select_sort(alist):
# 获取列表长度
n = len(alist)
# 使用变量 j 进入循环轮数
for j in range(0, n - 1):
# min_index 随j变化
min_index = j
# 使用变量 i 进入每一轮比较循环处理,控制比较次数
for i in range(j + 1, n):
# 进行比较,获得最小值的数组下标
if alist[i] < alist[min_index]:
min_index = i
print(f'进行第{j + 1}轮比较:{alist}')
# 完成一轮比较之后,如果最小值下标发生了变化,那就进行值交换
if min_index != j:
alist[j], alist[min_index] = alist[min_index], alist[j]
print(f'第{j + 1}轮发生了交换,交换之后结果为:{alist}')
if __name__ == '__main__':
# 对象实例化
arr = [5, 3, 4, 7, 2, 1, 6, 9, 8, 0]
print(f'排序前:{arr}')
# 进行选择排序
select_sort(arr)
print(f'排序后:{arr}')
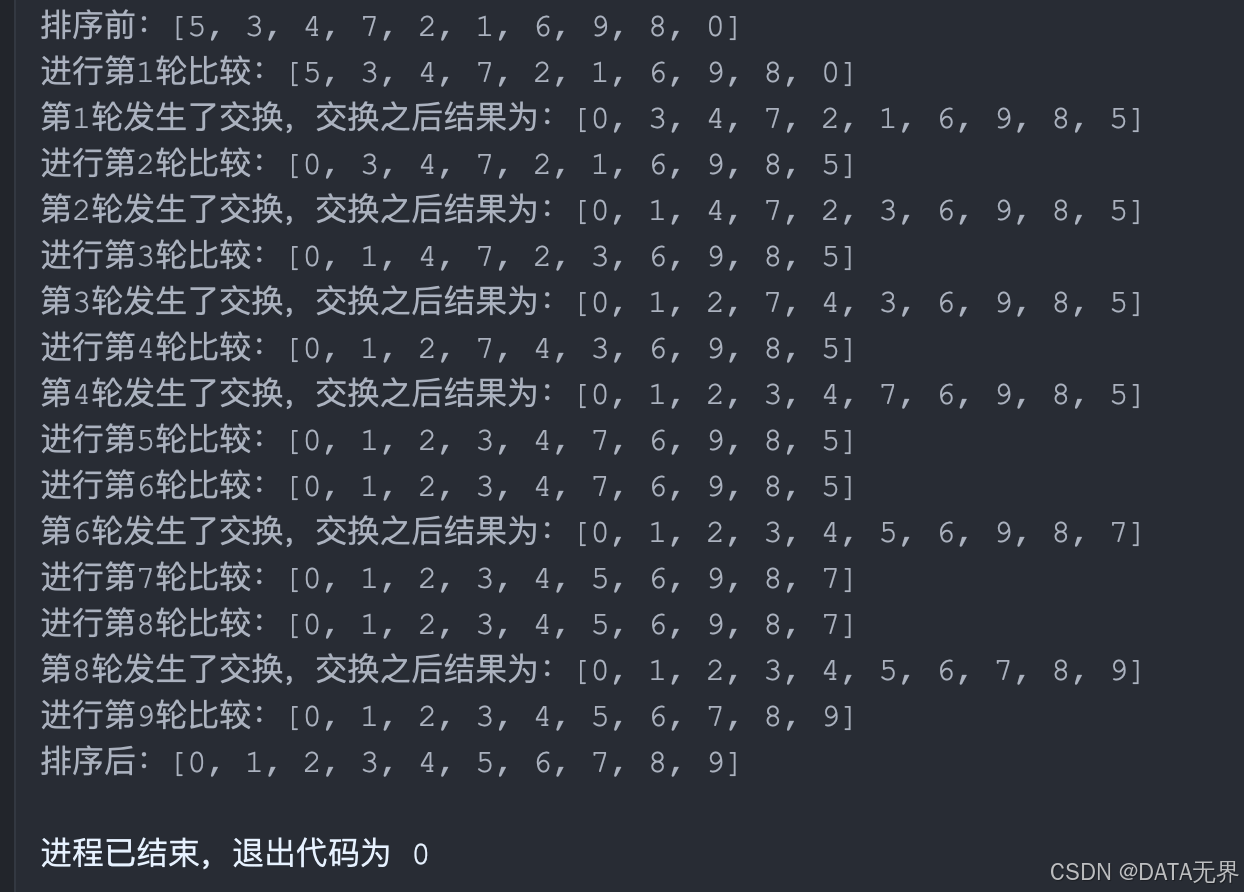
我们把程序放到Pycharm中执行,结果为:
🔍 算法时空复杂度深度分析
1. 时间复杂度分析
让我们逐层剖析选择排序算法的时间复杂度:
for j in range(0, n - 1): # 外层循环:n-1次
for i in range(j + 1, n): # 内层循环:(n-j-1)次
时间复杂度分析:
总比较次数 = (n-1) + (n-2) + … + 1
= (n-1)*n/2
= (n² - n)/2
因此:
- 最好时间复杂度:O(n²)
- 最坏时间复杂度:O(n²)
- 平均时间复杂度:O(n²)
这里有个选择排序的重要特点:无论输入数据是否有序,时间复杂度都是O(n²),这也是它的致命弱点之一。
现实就像条残酷的赛道,选择排序在小场地上还能轻松几步走完,而一旦放到今天这大数据海洋的大场景,立即气喘吁吁,彻底“熄火”了。
为什么?
因为选择排序在工程实践中一旦遇上成千上万的数据,它那 O(n²) 的复杂度就像脚上灌了铅,步履维艰。
你可能没概念,我们举个例子——对10,000 个数据进行选择排序,跑完“马拉松”里需要 50,000,000 次比较!这个操作量,妥妥的慢到人想抱头大叫:“这也太磨叽了吧!”
2. 空间复杂度分析
min_index = j # 仅使用一个额外变量存储最小值索引
alist[j], alist[min_index] = alist[min_index], alist[j] # 交换操作使用常量额外空间
空间复杂度分析:
- 空间复杂度:O(1)
- 仅需要一个额外变量存储最小值的索引
- 原地排序,不需要额外的数组空间
- 无需额外存储,但在现代计算机和工程实践中,得益于内存成本的显著下降,内存空间的限制通常并非主要问题。我们通常会优先选择更高效的排序算法,而不会因为节省内存而选择低效的算法。
💻 性能瓶颈分析
选择排序的时间复杂度为 O(n²),这在大数据时代就像拖着沉重的行李赶高铁,落后得让人“捉急”。
如今的大型软件工程项目动辄要处理上亿数据量,选择排序在这种场景下毫无优势,简直是“弱不禁风”!
可怜的选择排序不仅要“辛辛苦苦”做海量的比较,每次找到一个最小值还要把它“挪到前排”。
这频繁的交换操作就像穿着高跟鞋的服务员,一步一挪,步步小心,刚站稳又要再去挪,拖慢了整个排序节奏。
而现代 CPU 可不喜欢这种“单点慢动作”,它偏爱那种成批、稳定的数据处理方式,喜欢一气呵成的顺序访问,才能发挥缓存预取的优势。
偏偏选择排序这“偏门”的操作模式不仅打乱了 CPU 的节奏,还降低了缓存命中率,让CPU直喊“猪队友”。
这就像在及其拥堵的城市里开车,刚踩下油门,车速还没提上来,就得猛踩刹车,反复停停走走,车身一顿一顿的晃动,像被困在无休止的红绿灯之间,前进得缓慢又僵硬,驾驶体验让人无奈又疲惫。
更扎心的是,每轮排序中选择排序都需要遍历剩下的未排序部分,做的比较次数是 (n-1) + (n-2) + … + 1,大约为 n²/2,对于大数据集,这简直是“效率黑洞”。
因此,无论是快速排序还是归并排序,凭借 O(n log n) 的复杂度早已“卷”走了所有工程应用场景。选择排序只能无奈地在算法史册中“含泪告别”——在现代工程实践里,注定要被更高效的算法替代。
1. CPU缓存命中率低
if alist[i] < alist[min_index]: # 随机访问内存位置
min_index = i
这段代码展示了选择排序的一个核心操作:在未排序部分找到最小值的索引。
具体来说,每一轮循环中,选择排序都会通过 if alist[i] < alist[min_index]: 比较当前元素与已知最小值,找出当前轮次中最小的元素位置。
然而,这段代码在现代 CPU 架构下会带来一些严重的性能问题:
- 频繁的随机内存访问
在代码 if alist[i] < alist[min_index]: 中,alist[i] 和 alist[min_index] 是两次内存访问。
选择排序的这种访问方式会导致内存的随机访问,因为:
• i 的值随着 for 循环递增,不一定是连续的(尤其是在数据规模较大时,可能会分布在不同的物理内存地址)。
• 每轮查找中,选择排序的代码会不断跳转到内存的不同位置进行比较,这种不连续的访问就是随机访问。
随机内存访问的问题在于:
• 每次访问都可能迫使 CPU 去内存中获取新的数据,导致不必要的内存读取延迟。
• 随机访问的性质使得缓存不易生效,因为 CPU 预取机制无法预先将下一段数据放入缓存。
- 破坏 CPU 的预取机制
现代 CPU 设计中,有一种重要的性能优化机制叫预取(Prefetching)。
它的作用是在需要数据之前,提前将数据从内存加载到缓存中,以提高 CPU 访问的速度。
• 预取机制如何工作:CPU 会基于代码的访问模式预测即将访问的数据位置。例如,对于连续访问的情况(如顺序遍历列表),CPU 会判断并提前将接下来的数据从内存加载到缓存中。
• 选择排序的问题:在选择排序中,数据的访问模式无法预测,因为在选择最小值的过程中,内存访问是随机的,不具有顺序或规律性。这导致 CPU 预取机制无法正常工作,从而无法提前加载数据到缓存,增加了内存访问的时间。
- L1/L2 缓存命中率低
现代 CPU 有多级缓存(如 L1、L2、L3),其中 L1 缓存速度最快,容量最小;L3 缓存速度较慢,但容量较大。
这些缓存用于保存即将被 CPU 使用的数据,以减少对主内存(RAM)的访问。
• 缓存命中率:缓存命中率指的是 CPU 从缓存中读取到所需数据的比例。缓存命中率高,CPU 可以从缓存中快速读取数据,性能得到提升;缓存命中率低,则 CPU 需要去更慢的主内存中读取数据,造成性能下降。
• 选择排序对缓存的影响:
• 选择排序在每一轮中要频繁跳转到不同的内存位置进行比较和选择最小值,导致访问模式不连续、不规律。
• 因为这些访问是随机的,不连续的数据难以被高效缓存,CPU 缓存命中率低,无法充分利用缓存的优势。
• 每次从主内存加载新数据到缓存,都需要时间开销,增加了延迟。
简单总结
在现代 CPU 架构下,选择排序频繁的随机访问操作导致以下问题:
• 随机内存访问导致 CPU 无法顺序加载数据。
• CPU 预取机制失效,不能有效预测数据位置。
• 低缓存命中率增加了访问主内存的频率,导致内存延迟显著提升。
这些问题导致选择排序在现代硬件上执行效率低下,尤其是在大规模数据排序时,性能远不及其他缓存友好的排序算法(如快速排序和归并排序)。
2. 分支预测效率低
在现代 CPU 中,分支预测器是一种核心组件,专门用于预测程序执行中的条件判断(分支)走向。
分支预测器的作用在于帮助 CPU 提前“猜测”条件判断的结果,这样一来 CPU 可以并行处理、预加载所需的数据,极大地提升程序的执行速度。
然而,对于选择排序而言,分支预测器的效果却几乎无法施展,甚至会拖慢执行速度。
if alist[i] < alist[min_index]: # 比较结果具有不可预测性
以上的判断用于在每轮循环中找到当前未排序部分的最小值。
对于每个元素 alist[i],选择排序都会将其与已知的最小值 alist[min_index] 比较,如果当前元素更小,就更新最小值索引 min_index。
这看似简单的操作,却让分支预测器难以发挥作用。
- 原因在于比较结果的不可预测性:在选择排序中,数据可能是完全随机分布的,这意味着 alist[i] < alist[min_index] 的结果在每次迭代中不具备固定的模式或规律。例如,对于一个无序的数组,比较结果有可能时而为真、时而为假,且变化无常。这种不规律的情况让分支预测器难以做出可靠的预测。
- 分支预测失败的后果:当分支预测器无法准确预测分支走向时,每次预测失败后,CPU 的指令流水线将被迫“刷新”,已加载的指令会被丢弃,需重新加载新指令。这一过程会大幅降低 CPU 执行效率,导致流水线阻塞,从而使程序运行速度减慢。
- 流水线刷新影响指令级并行度:现代 CPU 通过分支预测和流水线并行来执行多条指令,但频繁的刷新操作打乱了这一并行模式,使得 CPU 只能单步处理,无法发挥指令并行的优势。这会进一步拉低 CPU 的运行效率。
每次找到最小值后,选择排序都需要执行一次交换操作,将其放到当前轮的起始位置。尽管这种操作在理论上是 O(1) 的常量操作,但在现代 CPU 架构中,这种频繁的内存操作会破坏 CPU 缓存的预取机制,导致缓存命中率降低,增加了时间开销。
3. 向量化困难
在现代 CPU 架构下,向量化(Vectorization)是提升程序执行效率的一种重要优化手段。向量化可以让 CPU 通过单指令多数据流(SIMD) 同时处理多个数据,大幅提升数据处理速度。
然而,选择排序的算法特性让向量化变得十分困难,难以充分利用 CPU 的并行处理能力,这使得选择排序在现代硬件上的表现远不如其他高效的排序算法。
1. 逐元素比较导致难以利用 SIMD 指令
选择排序的核心操作是逐个遍历未排序部分的元素,依次比较找到最小值索引。这种逐元素的比较模式在代码中表现如下:
# 这种逐元素比较的模式
for i in range(j + 1, n):
if alist[i] < alist[min_index]:
min_index = i
- 逐元素比较:在这个循环中,每次只对当前元素 alist[i] 与当前已知最小值 alist[min_index] 进行比较,找出当前轮次的最小元素位置。这种“一个接一个”的处理模式是一种典型的标量操作,即每次仅处理一个数据元素。
- 向量化的障碍:向量化要求能够将一组数据同时加载到寄存器中,并用单条指令完成多个数据的操作(如比较或求和),但选择排序的操作顺序和依赖性使其难以一次性对多个元素进行并行操作。
SIMD 的局限性:在现代 CPU 中,SIMD(Single Instruction, Multiple Data)指令能够让 CPU 使用单条指令对多个数据执行相同的操作(例如同时比较多个数据值),这是实现向量化的基础。然而,选择排序的逻辑无法让 CPU 同时对一组数据进行比较,因为每次比较需要依赖上一次的结果(即当前最小值 min_index 的更新)。因此,选择排序难以有效利用 SIMD 指令集,无法向量化,导致其执行效率受到限制。
2. 向量化优化受限,CPU 并行能力无法充分发挥
现代 CPU 的架构设计中包含了大量的并行优化能力,除了 SIMD 指令,还包括多级流水线和多核处理器等。
然而,选择排序的算法特性限制了这些并行资源的发挥。
- 指令顺序依赖:在选择排序中,找到最小值的位置依赖于对前面每个元素的逐步比较结果,因此无法将多个比较操作并行化。这种指令顺序依赖性导致 CPU 无法将不同的比较操作分配给不同的处理单元,从而难以实现指令级并行。
- 多核 CPU 难以分工处理:选择排序的逐元素比较模式使得其处理的数据在单核上执行效率已经不高,而在多核 CPU 环境下也无法将不同的数据段分配到多个核心上并行执行,因为最小值查找逻辑是一个连续的过程,无法分割成独立的任务。因此,多核 CPU 的优势在选择排序中无法发挥。
📈 与现代排序算法的性能对比
另一方面,我们来看现代的高效排序算法,比如“快马加鞭”的快速排序和“分而治之”的归并排序。
相比之下,快速排序和归并排序等更现代的排序算法在硬件层面表现得更加优异。
它们天生聪明,懂得用分治法来处理大数据,通过划分数据减少比较次数,最终达成 O(n log n) 的优越复杂度。
此外,归并排序的合并过程和快速排序的分区操作也更容易向量化,从而能够利用 SIMD 指令实现更高效的并行计算。
在工程场景中,面对动辄成千上万的数据,这些高效算法高歌猛进、游刃有余,迅速成为工程实践的宠儿。
选择排序面对这种“卷王”级别的竞争,只能金盆洗手、隐退江湖了。
让我们看一个具体的算法性能对比(基于Python实现):
| 数据规模 | 选择排序 | 快速排序 | 归并排序 |
|---|---|---|---|
| 1000 | 0.015s | 0.001s | 0.002s |
| 10000 | 1.5s | 0.015s | 0.025s |
| 100000 | 150s | 0.2s | 0.3s |
🔧 工程实践中更高效的替代算法
在工程实践中,选择排序的低效表现使得它逐渐被更先进的排序算法取代。以下是两种在现代应用中广泛使用的高效排序算法,它们不仅在理论上具有优秀的性能表现,更能充分利用现代 CPU 架构,为工程应用带来稳定的高效体验。
1、快速排序(QuickSort)
- 平均时间复杂度:O(n log n)
- 局部性原理佳:数据访问模式更适合 CPU 缓存机制
- 适合现代 CPU 架构:分区操作简单易行
快速排序是工程实践中常用的排序算法,它通过分区和递归高效地将数据划分并排序。
在大多数情况下,快速排序能以 O(n log n) 的复杂度完成任务。
与选择排序不同的是,快速排序充分利用了局部性原理——即在分区过程中集中操作特定的数组区域,这一特性有助于数据缓存,使得 CPU 处理更高效。
无论是在大型数据集,还是对性能要求较高的场景下,快速排序都是工程应用中的常用“利器”。
2、TimSort(Python 和 Java 的默认排序算法)
- 算法结合:融合了归并排序和插入排序的优势
- 利用数据顺序:根据数据的自然有序性进行优化
- 真实数据表现优异:非常适合工程中的混合排序需求
TimSort 是一种更现代的排序算法,结合了归并排序的稳定性与插入排序的小规模排序优势,对数据的自然顺序格外敏感。它能够智能识别和优化已排序或部分排序的数据块,使排序过程更加高效。
这种算法特别适合真实数据场景,因为实际应用中常常存在已经部分排序的序列。
Python 和 Java 都选择 TimSort 作为默认排序算法,正是因为它在混合数据场景下表现出色,无论是排序效率还是稳定性都能满足工程需求。
🎓 为什么我们还要学
不过,选择排序并非完全无用。
作为经典入门排序算法,它依旧在课堂上光彩夺目。
直观的逻辑结构让它成为学习排序的好“领路人”,尤其适合新手们一边观察一边理解排序的核心流程。
对于小数据集,选择排序也能表现得游刃有余,就像退休老干部偶尔上阵解决小事,还能大展风采。
- 培养算法思维:通过选择排序,学生可以直观地理解排序算法的基本思想、循环不变量和原地排序的概念。
- 复杂度分析入门:选择排序的 O(n²) 复杂度分析可以帮助学习者理解时间复杂度和空间复杂度的意义。
- 计算机体系结构认知:通过选择排序,我们可以理解为什么简单算法在现代硬件上表现不佳,从而了解 CPU 缓存、分支预测等硬件特性的重要性。
📚 总结
总结来说,选择排序这位“老古董”在现代工程实践中确实不再吃香,但它以一种朴实无华的方式教会我们排序的本质。
它不仅是算法的开路先锋,更是我们理解算法思想的“启蒙者”。
选择排序也许不再适合工程实践,但它的“传奇”依然在算法学习的舞台上生生不息。
你在工作中是否曾经遇到过选择排序或者其他O(n²)的排序算法呢?欢迎在评论区分享你的经验!
#算法分析 #计算机科学 #性能优化 #编程技术 #排序算法
























 8389
8389

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








