机器学习与深度学习数学基础系列文章目录
第一章 一文速通概率论与数理统计必备基础
第二章 一文速通机器学习与深度学习微积分必备基础
第三章 一文速通高等数线性代数部分
第四章 一文速通优化算法部分
机器学习与深度学习数学基础(一文速通概率论与数理统计必备基础)
前言
适合有一定数学基础的同学或搭配《概率论与数理统计》相关课程视频速刷
一、初识概率论
1.1 什么是概率论与数理统计?
生活中大部分事情分为两类:
| 确定性现象 | 随机性现象 |
|---|---|
| 条件完全决定结果 | 条件不完全决定结果 |
- 其中的随机性现象
随机现象具有: 不确定性 与 统计规律性
- 概率论 = 从数量上研究随机现象的统计规律性的科学
- 数理统计 = 从应用角度研究处理随机数据,建立有效统计方法进行统计推理
1.2 事件与概率
- 定义一: 可重复、每次实验结果随机、所有可能结果预先可知的实验称为随机试验–E
- 定义二: 所有可能结果的集合称为实验E的样本空间
- 定义三: 样本空间内的子集称为事件
- 定义四: N次实验中,事件A发生次数称为 频数,频数与N比值为 频率,当频率趋于某个值则该值为事件A发生 概率(频率学派)
- 频率学派反映了机器学习思想:从实验数据中寻找真实模型
1.3 古典概型与几何概型
古典概型(等可能概型):
- 有限性:基本事件总数有限
- 等可能性:每个基本事件发生可能相同
古典概型概率计算公式:
几何概型:
把有限个样本点推广到无限个样本点的场合,即对于一个随机试验,无穷多个样本点出现是等可能的,且具有非零的,有限的集合度量即 0 < m ( 样本空间 ) < 无穷 0<m(样本空间)<无穷 0<m(样本空间)<无穷,则称该实验为几何概型的
分母为样本空间中的度量分子是构成事件A的子区域度量
二、概率计算
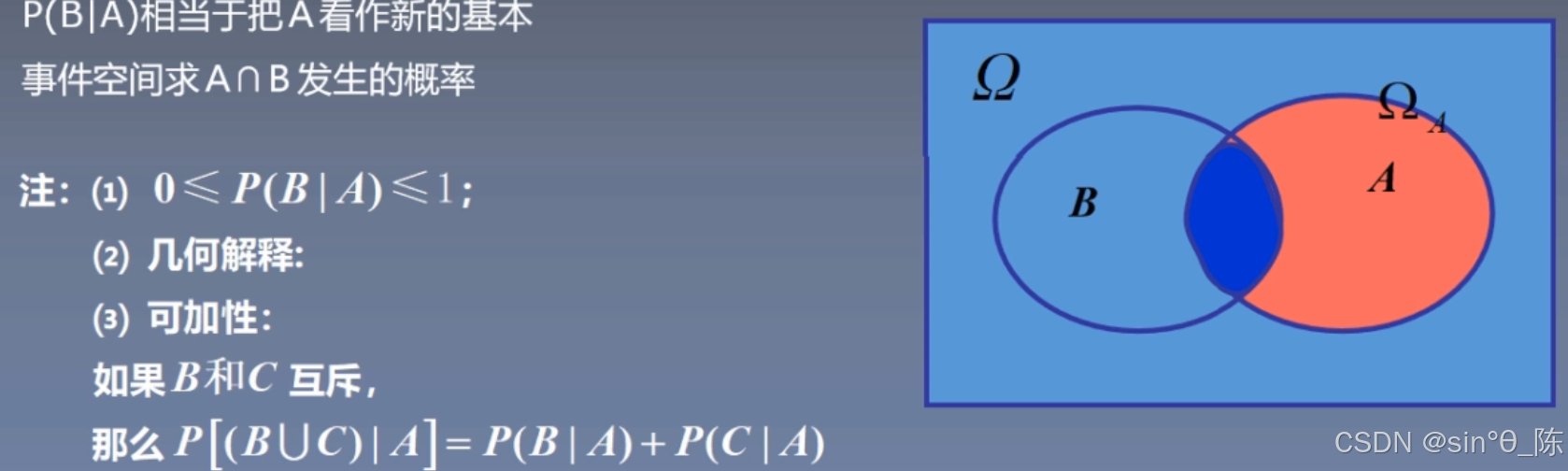
2.1 条件概率
一般地,设 A、B 为两个事件,且 P(A) > 0,称:
P ( B ∣ A ) = P ( A B ) P ( A ) P(B | A) = \frac{P(AB)}{P(A)} P(B∣A)=P(A)P(AB)
为在事件 A 发生的条件下,事件 B 发生的条件概率 P(B | A) 。
读作:A 发生的条件下 B 的概率。
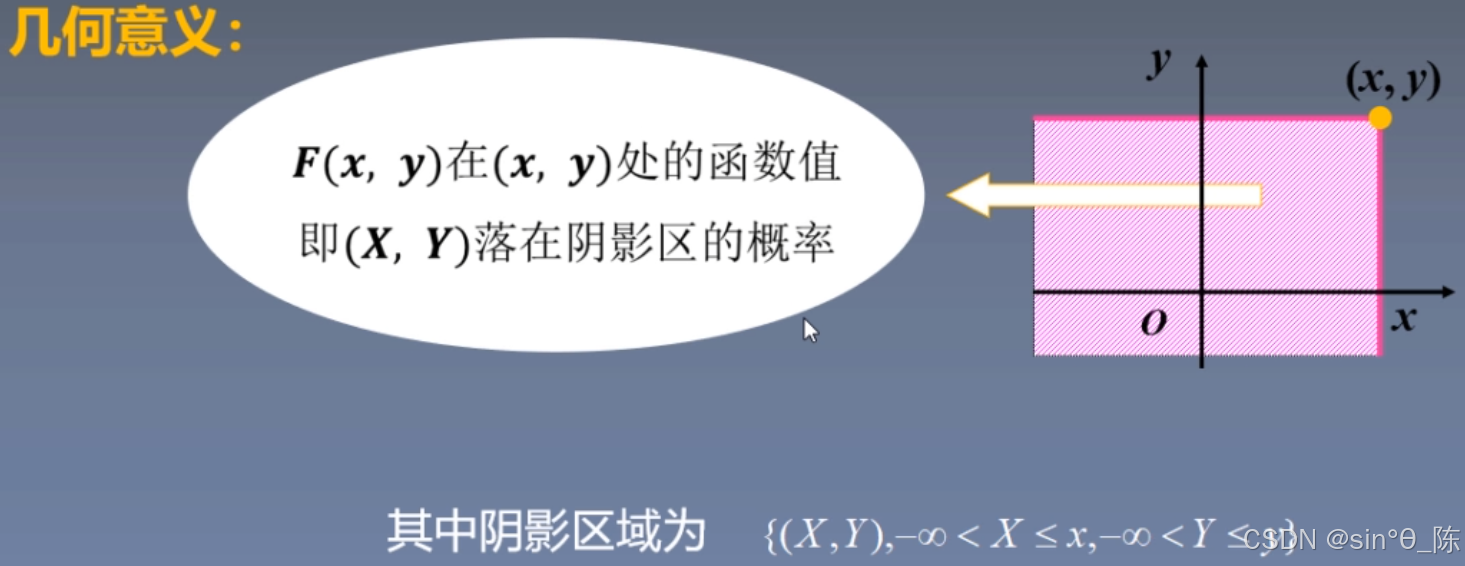
条件概率的几何意义;
乘法公式:
排列与组合:
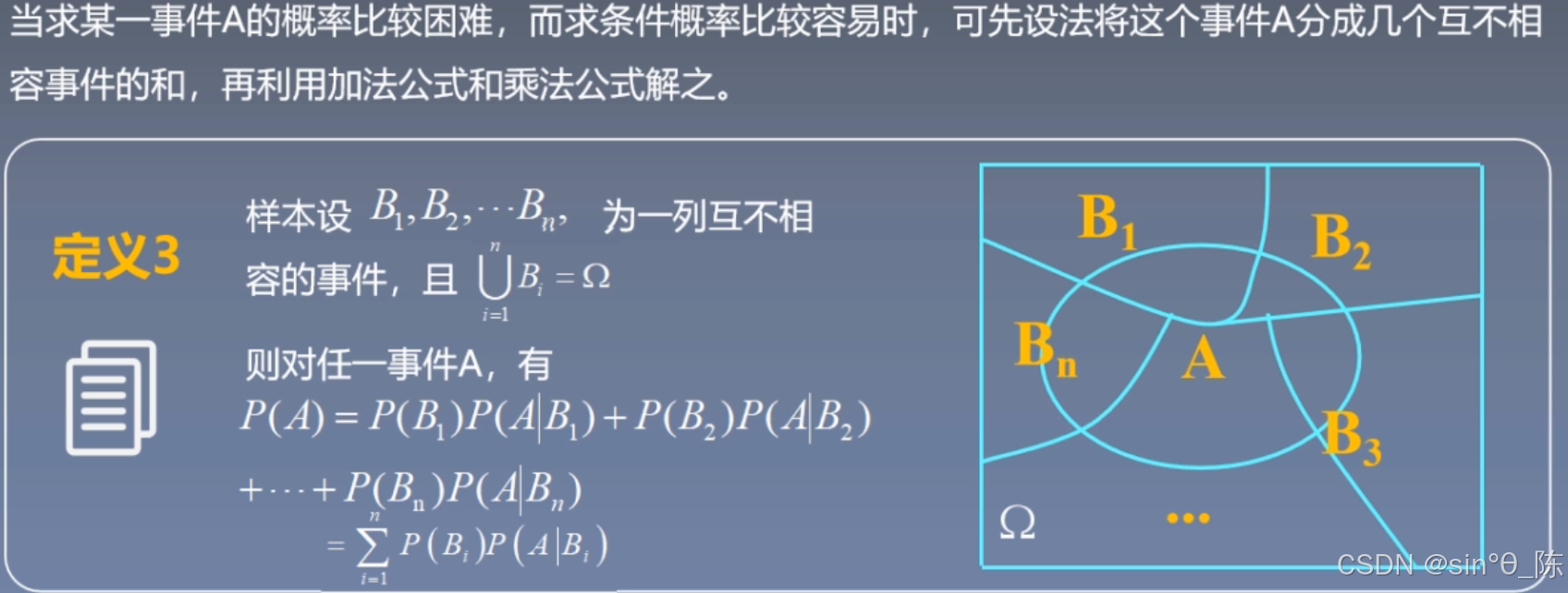
2.2 全概率公式
三、分布与分布特点
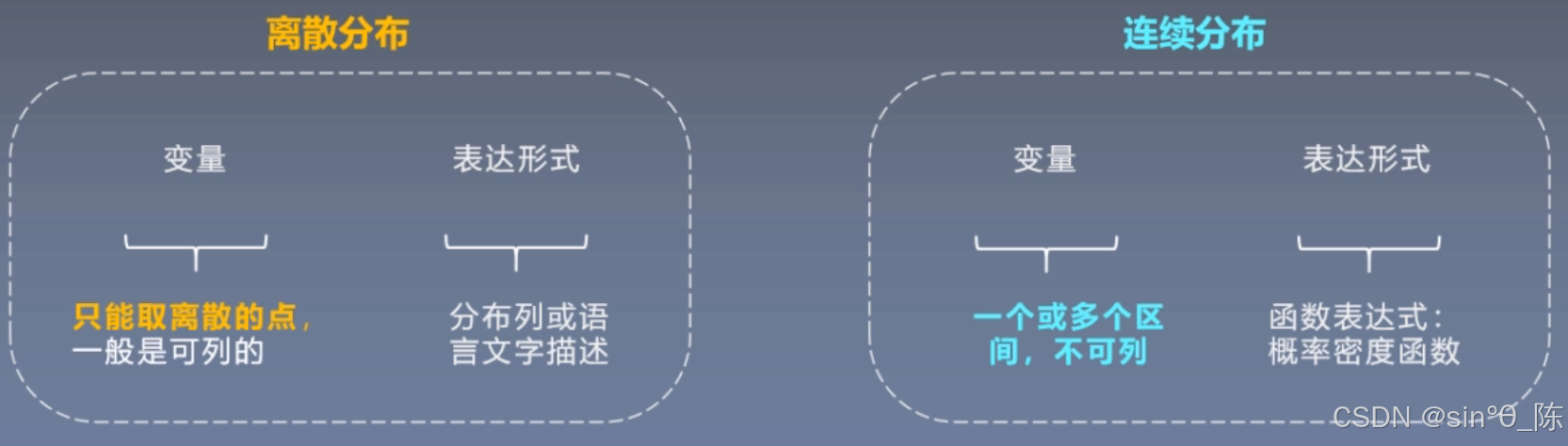
3.1 概率分布类型
- 离散分布 VS 高斯分布
【最简单的离散分布就是抛硬币,也即是伯努利分布:X只取 0 0 0 和 1 1 1 两个值, P ( X = 1 ) = p , P ( X = 0 ) = 1 − p P(X = 1) =p,P(X = 0) = 1 - p P(X=1)=p,P(X=0)=1−p】
【稍微复杂一点的是二项分布:进行 n 次独立重复试验后,成功 k 次的概率公式为: P ( X = k ) = ( n k ) p k ( 1 − p ) n − k P(X = k) = \binom{n}{k} p^k (1 - p)^{n - k} P(X=k)=(kn)pk(1−p)n−k】
- p^k 表示 k 次成功的概率。
- (1 - p)^{n - k} 表示 n - k 次失败的概率。
3.2 期望与方差
期望的定义
【期望反映了数值的均值水平,这里的级数是为了更加严格的数学定义】
期望的性质(Expectation Feature)
- E© = C
2. E(aX) = aE(X)
3. E(X + Y) = E(X) + E(Y)
4. 当 X, Y 相互独立时,E(XY) = E(X)E(Y)
方差的定义*
【方差反映了分布的离散水平】
数据归一化
【在机器学习中常需要数据归一化,它通过特定的方法 将数据的取值范围调整到一个特定的区间,通常是 [0,1] 或 [-1,1],使得不同特征的数据具有相同的尺度,以便更好地进行数据分析和模型训练等工作。以下是一个简单常用的归一化方法】
3.3 高斯分布
四、概率分布进阶
4.1 分布函数
4.2 均匀分布
4.3 指数分布
【指数分布具有无记忆性:如果一个随机变量 ( X ) (X) (X) 表示某个事件发生的时间,并且它服从指数分布,那么在时间 ( t ) (t) (t) 之后发生该事件的剩余时间只与 ( t ) (t) (t) 无关,且仍然服从同样的指数分布。换句话说,事件过去的时间不会影响未来的发生概率】
五、联合分布
5.1 二位随机变量及联合概率分布
5.2 边缘分布
六、主成分分析法
6.1 多维分布与协方差
为什么需要协方差?
协方差性质:
协方差矩阵:
【矩阵知识补充:向量的转置就是将“竖向排列”的列向量变为“横向排列”的行向量,或者将行向量转变为列向量。】
如果 X 是一个列向量: X = ( X 1 X 2 ⋮ X n ) X = \begin{pmatrix} X_1 \\ X_2 \\ \vdots \\ X_n \end{pmatrix} X= X1X2⋮Xn
它是一个 n × 1 n \times 1 n×1 的矩阵,那么它的转置 X T X^T XT 是一个行向量:
X T = ( X 1 X 2 ⋯ X n ) X^T = \begin{pmatrix} X_1 & X_2 & \cdots & X_n \end{pmatrix} XT=(X1X2⋯Xn)
也就是一个 1 × n 1 \times n 1×n 的矩阵。
6.2 主成分分析法(PCA)
- PCA的意义
机器学习主要问题:维度灾难
PCA:在力求数据信息丢失最少的原则下,对高维的变量空间降为维,即研究指标体系的少数几个线性组合,并且这几个线性组合所构成的综合指标尽可能多的保留原来指标变异方面的信息,这些综合指标就称为主成分

- PCA推导


协方差矩阵与特征值分解详细说明
【在PCA推导中,协方差矩阵 和 特征值 分解是核心的数学工具。我们将分别解释这两部分的基本概念和在PCA中的作用。】
- 协方差矩阵
协方差矩阵用于衡量多个变量之间的关系。在数据集中,假设我们有 p 个变量,每个变量有 n 个观测值。我们可以计算这些变量之间的协方差,生成一个 p × p p \times p p×p 的矩阵。
- 协方差矩阵的定义:
设数据矩阵 X X X 是一个 n × p n \times p n×p 的矩阵,表示 n n n 个样本和 p p p 个特征,协方差矩阵 Σ X \Sigma_X ΣX 定义如下:
Σ X = [ σ 1 2 σ 12 … σ 1 p σ 21 σ 2 2 … σ 2 p ⋮ ⋮ ⋱ ⋮ σ p 1 σ p 2 … σ p 2 ] \Sigma_X = \begin{bmatrix} \sigma_1^2 & \sigma_{12} & \dots & \sigma_{1p} \\ \sigma_{21} & \sigma_2^2 & \dots & \sigma_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ \sigma_{p1} & \sigma_{p2} & \dots & \sigma_p^2 \\ \end{bmatrix} ΣX= σ12σ21⋮σp1σ12σ22⋮σp2……⋱…σ1pσ2p⋮σp2 - σ i 2 \sigma_i^2 σi2:第 i 个变量的方差,表示该变量的离散程度。
- σ i j \sigma_{ij} σij:变量 i 和变量 j 的协方差,表示它们之间的线性关系。协方差为正表示正相关,为负表示负相关。
协方差矩阵的主要特点是 对称性,即 σ i j = σ j i \sigma_{ij} = \sigma_{ji} σij=σji。
协方差的计算公式:给定两个变量 X i X_i Xi 和 X j X_j Xj,它们的协方差 σ i j \sigma_{ij} σij 计算公式为:
σ i j = 1 n − 1 ∑ k = 1 n ( X i k − μ i ) ( X j k − μ j ) \sigma_{ij} = \frac{1}{n-1} \sum_{k=1}^{n} (X_{ik} - \mu_i)(X_{jk} - \mu_j) σij=n−11k=1∑n(Xik−μi)(Xjk−μj)
其中, μ i \mu_i μi 和 μ j \mu_j μj 分别是 X i X_i Xi 和 X j X_j Xj 的均值。
- 特征值与特征向量
特征值和特征向量是线性代数中用于解构矩阵的工具。协方差矩阵的特征值和特征向量表示了数据中不同方向上的变异程度和方向。
- 特征值分解:
对于协方差矩阵 \Sigma_X,可以通过特征值分解将其表示为:
Σ X = U Λ U T \Sigma_X = U \Lambda U^T ΣX=UΛUT- U U U:矩阵的特征向量矩阵,表示新坐标系的方向。
- Λ \Lambda Λ:对角矩阵,包含协方差矩阵的特征值 λ 1 \lambda_1 λ1, λ 2 \lambda_2 λ2, … \dots …, λ p \lambda_p λp,每个特征值表示对应特征向量方向上的方差大小。
- PCA中的特征值分解
在PCA中,协方差矩阵的特征值和特征向量是用来确定数据的主成分的。
- 特征值 λ i \lambda_i λi 表示主成分方向上的方差大小。较大的特征值意味着该方向上的数据变化较大,是更重要的主成分。
- 特征向量 u i u_i ui 则表示主成分的方向,数据可以沿着这些特征向量方向进行投影。
【通过对协方差矩阵进行特征值分解,PCA可以识别数据中变化最大的方向,并将数据投影到这些方向上,实现 降维 和 特征提取】
- 特征值分解示例
协方差矩阵 \Sigma_X 的特征值分解可以表示为:
U T Σ X U = [ λ 1 0 … 0 0 λ 2 … 0 ⋮ ⋮ ⋱ ⋮ 0 0 … λ p ] U^T \Sigma_X U = \begin{bmatrix} \lambda_1 & 0 & \dots & 0 \\ 0 & \lambda_2 & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dots & \lambda_p \\ \end{bmatrix} UTΣXU= λ10⋮00λ2⋮0……⋱…00⋮λp
- U 是协方差矩阵的正交特征向量矩阵,表示新坐标系。
- \lambda_1, \lambda_2, \dots, \lambda_p 是特征值,对应不同方向上的方差。
【在PCA中,我们通常选择前几个最大的特征值及其对应的特征向量来构建主成分,从而减少维度并保留数据中的主要信息】
总结:
PCA通过对协方差矩阵进行特征值分解来找到数据中最重要的方向。这使得我们可以 减少数据维度,同时保留数据的主要特征。这一过程的 核心是协方差矩阵的构建和对其进行的特征值分解。
七、概率论与信息论(中心极限定理与矩估计)
7.1 中心极限定理
- 入门理解 —— 切比雪夫不等式(chebyshev inequality):
- 中心极限定理
【请重点理解:中心极限定理是阐述大量随机变量之和的极限分布,是正态分布一系列定理的总称,中心极限定理提供了用样本平均数估计总体平均数的理论依据】- 【拓展:】
7.2 矩估计(一种基础的参数估计方法)



【一般只使用四阶以下矩】
在矩估计法中,矩主要分为原点矩和中心矩。
什么是矩?
- 原点矩
- 定义:对于随机变量 X X X,如果它的k阶矩 E ( X k ) E(X^k) E(Xk) 存在,那么称 E ( X k ) E(X^k) E(Xk) 为 X X X 的k阶原点矩,记为 μ k \mu_k μk。
- 例如:
- 一阶原点矩是 μ 1 = E ( X ) \mu_1 = E(X) μ1=E(X),即随机变量 X X X 的 数学期望。
- 二阶原点矩是 μ 2 = E ( X 2 ) \mu_2 = E(X^2) μ2=E(X2),它与随机变量的方差 σ 2 = E [ ( X − E ( X ) ) 2 ] \sigma^2 = E[(X - E(X))^2] σ2=E[(X−E(X))2] 有一定关系,具体为 μ 2 − μ 1 2 = E ( X 2 ) − ( E ( X ) ) 2 \mu_2 - \mu_1^2 = E(X^2) - (E(X))^2 μ2−μ12=E(X2)−(E(X))2。
- 中心矩
- 定义:若 E [ ( X − E ( X ) ) k ] E[(X - E(X))^k] E[(X−E(X))k] 存在,则称其为 X X X 的 k k k 阶中心矩,记为 M k M_k Mk。
- 例如:
- 二阶中心矩 M 2 = E [ ( X − E ( X ) ) 2 ] M_2 = E[(X - E(X))^2] M2=E[(X−E(X))2],就是随机变量 X X X 的方差 σ 2 \sigma^2 σ2。
一维随机变量的矩的几何意义:
- 对于一个一维随机变量 X X X,其原点矩 E ( X k ) E(X^k) E(Xk) 有如下几何意义:
- 一阶原点矩 E ( X ) E(X) E(X) 表示随机变量 X X X 的 重心 或 期望位置。可以理解为,如果把随机变量的取值看作是概率分布的质量点,那么一阶原点矩就是这些质量点的重心坐标。
- 二阶原点矩 E ( X 2 ) E(X^2) E(X2) 与随机变量的方差有密切关系。它反映了 随机变量取值的分散程度,数值越大,说明取值分布越分散,偏离期望值的幅度越大。
二维图像(以平面图形为例)的矩的几何意义:
- 对于一个二维平面图形,其矩具有以下几何意义:
- 零阶矩 M 0 M_0 M0 表示图形的面积。可以通过对图像中所有像素的亮度值进行求和得到。
- 一阶矩 M 10 M_{10} M10 和 M 01 M_{01} M01 分别表示图形在x轴和y轴方向上的重心坐标。类似于一维随机变量的k阶原点矩,这两个矩反映了图形在平面上的质量分布中心。
- 二阶矩 M 20 M_{20} M20、 M 02 M_{02} M02 和 M 11 M_{11} M11 用于描述图形的形状和分布特征。例如, M 20 M_{20} M20 和 M 02 M_{02} M02 以及混合二阶矩 M 11 M_{11} M11 可以组成一个矩阵,这个矩阵描述了图形在x轴和y轴方向上的方差与协方差,从而描述图形的形状及方向。
| 优点 | 缺点 |
|---|---|
| 计算相对简单,只需要计算样本矩并建立方程求解即可 | 矩估计法有时不是最有效的估计方法,可能存在估计的精度不高的情况 |
| 不依赖于总体分布的具体形式,只要总体矩存在,就可以使用矩估计法 | 对于一些复杂的分布,可能难以计算总体矩或者建立方程求解 |
八、两大估计方法
8.1 极大似然估计(MLE)


【极大似然估计法在逻辑回归的参数估计中有较多应用,可以观看李航的数理统计分析的机器学习方法做更进一步了解】
- 极大似然估计法求法
-
- 写出极大似然函数
-
- 取对数
-
- 对似然函数对数求导
-
- 令导数等于0,求解方程
-
8.2 最大后验估计法
先验分布:
【在样本少的情况下如何加入先验信息?】
九、贝叶斯法则
9.1 贝叶斯公式(后验公式)
贝叶斯意义
9.2 共轭分布



十、信息论基础
10.1 信息熵(信息度量)


【重点内容:信息熵】
交叉熵
【交叉熵 在机器学习中常用于度量两个随机变量之间的 相似度】
10.2 互信息

10.3 KL散度(相对熵)

-
非负性: 相对熵恒为非负: K L ( P ∥ Q ) ≥ 0 KL(P \parallel Q) \geq 0 KL(P∥Q)≥0,且在 P = Q P=Q P=Q 时取0。
-
不对称性: K L ( P ∥ Q ) ≠ K L ( Q ∥ P ) KL(P \parallel Q) \neq KL(Q \parallel P) KL(P∥Q)=KL(Q∥P)















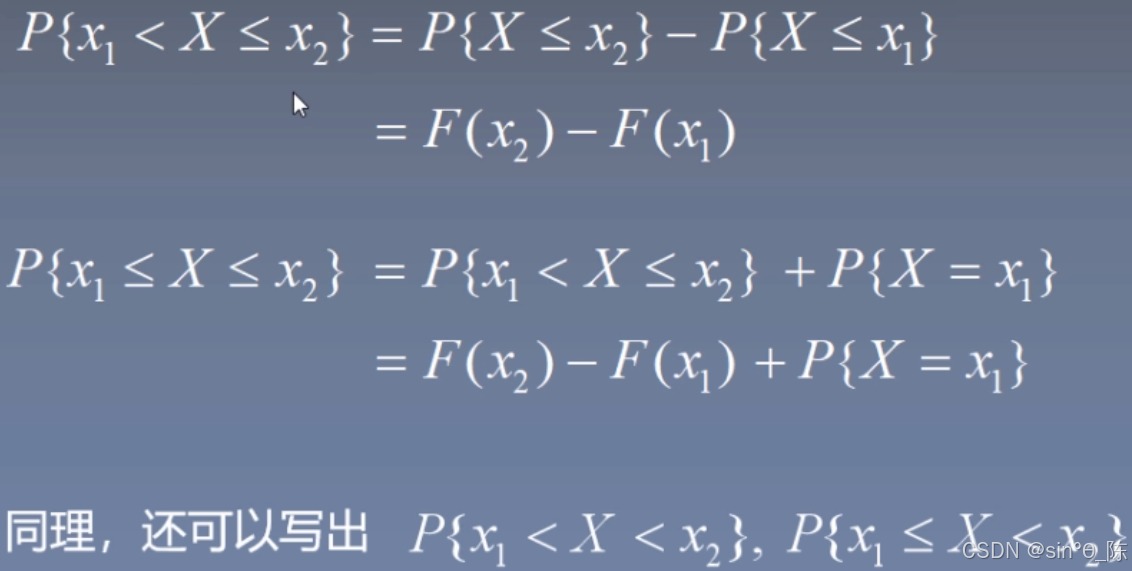














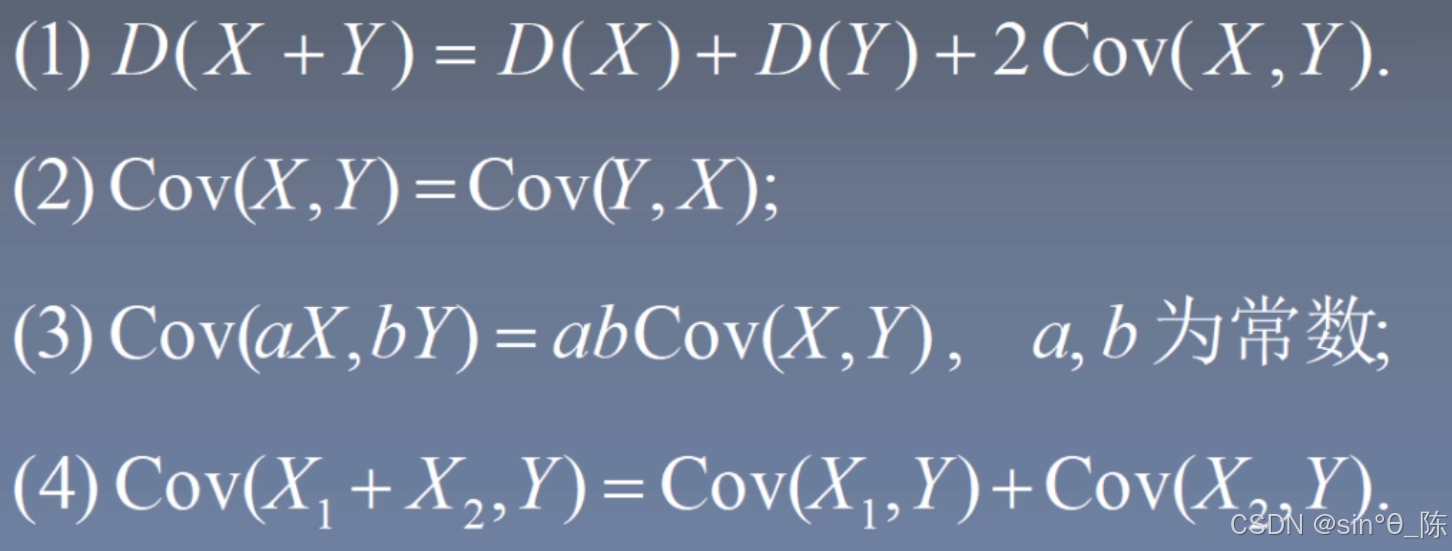





































 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








