一、介绍
Bloom Filter是一个有m bits的bit array，每一个bit位都初始化为0。并且定义有k个不同的hash function，每个都以uniform random distribution将元素hash到m个不同位置中的一个。n为要添加到bloomfilter里面的元素。p为错误率。所以相关的参数为：m n k p
二、原理分析
1、插入数据
插入流程：
- 对将要添加的元素执行k种不同的哈希函数
- 每次哈希后得到的结果为bit array的index
- 将每次得到的 bit array 中 index 的位置的bit值设为1
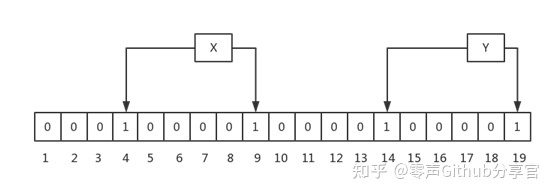
如上图，插入了2个元素，X和Y，X的两次hash取模后的值分别为4、9，因此，4和9位被置成1；Y的两次hash取模后的值分别为14和19，因此，14和19位被置成1。
2、查找数据
查询流程：
- 对将要添加的元素执行k种不同的哈希函数
- 每次哈希后得到的结果为bit array的index
- 将每次得到的 bit array 中 index 的位置对应的bit的值都为1，则返回元素可能存在，否则，返回元素不存在
为什么bit全部为1时，元素只是可能存在呢？
当然，如果情况如上图中只存在X，Y，而且两个元素hash后的值并不重复。那么这种情况就可以确定元素一定存在
但是，存在另一种情况。假设我们现在要查询Z元素，假设Z元素并不存在。但是正巧经过hash计算出来的位置为9,14。我们很清楚，这里的9是属于X元素的，14是术语Y元素的。并不存在Z。但是经过hash计算的结果返回值都是1。所以程序认为Z是存在的，但实际上Z并不存在，此现象称为false positive(不乐观)
3、为什么不能删除数据
BloomFilter中不允许有删除操作，因为删除后，可能会造成原来存在的元素返回不存在，这个是不允许的，还是以一个例子说明：
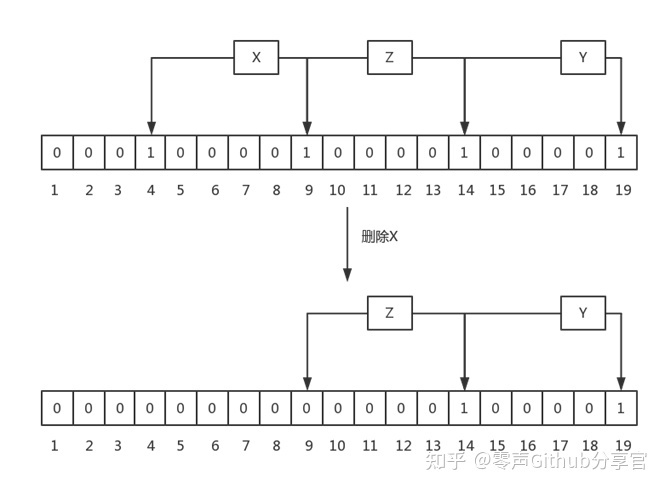
上图中，刚开始时，有元素X，Y和Z，其hash的bit如图中所示，当删除X后，会把bit 4和9置成0，这同时会造成查询Z时，报不存在的问题，这对于BloomFilter来讲是不能容忍的，因为它要么返回绝对不存在，要么返回可能存在。
问题：BloomFilter中不允许删除的机制会导致其中的无效元素可能会越来越多，即实际已经在磁盘删除中的元素，但在bloomfilter中还认为可能存在，这会造成越来越多的false positive。
三、优缺点分析
1、优点
常用的数据结构，如hashmap，set，bit array都能用来测试一个元素是否存在于一个集合中，相对于这些数据结构，BloomFilter有什么方面的优势呢？
相比于其它的数据结构，布隆过滤器在空间和时间方面都有巨大的优势。布隆过滤器存储空间和插入/查询时间都是常数（O(k)）。另外, 散列函数相互之间没有关系，方便由硬件并行实现。布隆过滤器不需要存储元素本身，在某些对保密要求非常严格的场合有优势。
- 对于hashmap，其本质上是一个指针数组，一个指针的开销是sizeof(void *)，在64bit的系统上是64个bit，如果采用开链法处理冲突的话，又需要额外的指针开销，而对于BloomFilter来讲，返回可能存在的情况中，如果允许有1%的错误率的话，每个元素大约需要10bit的存储空间，整个存储空间的开销大约是hashmap的15%左右（数据来自维基百科）
- 对于set，如果采用hashmap方式实现，情况同上；如果采用平衡树方式实现，一个节点需要一个指针存储数据的位置，两个指针指向其子节点，因此开销相对于hashmap来讲是更多的
- 对于bit array，对于某个元素是否存在，先对元素做hash，取模定位到具体的bit，如果该bit为1，则返回元素存在，如果该bit为0，则返回此元素不存在。可以看出，在返回元素存在的时候，也是会有误判的，如果要获得和BloomFilter相同的误判率，则需要比BloomFilter更大的存储空间
布隆过滤器可以表示全集，其它任何数据结构都不能；
- 全量存储但是不存储数据本身，适合有保密要求的场景
- 空间复杂度为O(m)，不会随着元素增加而增加，占用空间少
- 插入和查询时间复杂度都是 O(k), 不会随着元素增加而增加，远超一般算法。
2、缺点
但是布隆过滤器的缺点和优点一样明显。误算率是其中之一。随着存入的元素数量增加，误算率随之增加。但是如果元素数量太少，则使用散列表足矣。
另外，一般情况下不能从布隆过滤器中删除元素. 我们很容易想到把位数组变成整数数组，每插入一个元素相应的计数器加1, 这样删除元素时将计数器减掉就可以了。然而要保证安全地删除元素并非如此简单。首先我们必须保证删除的元素的确在布隆过滤器里面. 这一点单凭这个过滤器是无法保证的。另外计数器回绕也会造成问题。
- 相对于hashmap和set，BloomFilter在返回元素可能存在的情况中，有一定的误判率，这时候，调用者在误判的时候，会做一些不必要的工作，而对于hashmap和set，不会存在误判情况
- 对于bit array，BloomFilter在插入和查找元素是否存在时，需要做多次hash，而bit array只需要做一次hash，实际上，bit array可以看做是BloomFilter的一种特殊情况
在降低误算率方面，有不少工作，使得出现了很多布隆过滤器的变种。
- 存在误算率，数据越多，误算率越高
- 一般情况下无法从过滤器中删除数据
- 二进制数组长度和 hash 函数个数确定过程复杂
四、误算率计算
- 位数组中某一特定的位在进行元素插入时的 Hash 操作中没有被置位的概率是：
-
在所有 k 次 Hash 操作后该位都没有被置 “1” 的概率是：
-
如果我们插入了 n 个元素，那么某一位仍然为 “0” 的概率是：
-
该位为 "1"的概率是：
检测某一元素是否在该集合中。标明某个元素是否在集合中所需的 k 个位置都按照如上的方法设置为 “1”，但是该方法可能会使算法错误的认为某一原本不在集合中的元素却被检测为在该集合中（False Positives），该概率由以下公式确定：
如何使得错误率最小，对于给定的m和n，当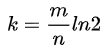 
的时候取值最小。关系如下图所示：
五、使用场景
布隆过滤器的巨大用处就是，能够迅速判断一个元素是否在一个集合中。因此他主要有如下三个使用场景:
1、去重
网页爬虫对URL的去重，避免爬取相同的URL地址
海量数据去重（如40亿QQ号去重问题）
2、敏感词快速识别
快速识别内容中是否含有敏感信息的场景
如识别垃圾邮件、垃圾短信、不文明发言中的敏感信息
3、防止缓存穿透
缓存穿透：当请求数据库中不存在的数据，这时候所有的请求都会打到数据库上，这种情况就是缓存穿透。如果当请求较多的话，这将会严重浪费数据库资源甚至导致数据库假死。
在大多应用中，当业务系统中发送一个请求时，会先从缓存中查询；若缓存中存在，则直接返回；若返回中不存在，则查询数据库。
BloomFilter解决缓存穿透的思路，这种技术在缓存之前再加一层屏障，里面存储目前数据库中存在的所有key，当业务系统有查询请求的时候，首先去BloomFilter中查询该key是否存在。若不存在，则说明数据库中也不存在该数据，因此缓存都不要查了，直接返回null。若存在，则继续执行后续的流程，先前往缓存中查询，缓存中没有的话再前往数据库中的查询。
六、JAVA中使用布隆过滤器
1、导包
Guava工具包提供了十分完善的BloomFilter实现。
<!-- https://mvnrepository.com/artifact/com.google.guava/guava -->
<dependency>
<groupId>com.google.guava</groupId>
<artifactId>guava</artifactId>
<version>27.0.1-jre</version>
</dependency>
2、源码分析
这里只分析布隆过滤器构造的过程
BloomFilter.create构造方法的核心参数主要有两个
-
expectedInsertions(参数n)：预期插入数，必须为正整数
-
fpp(参数p)：失误率，失误率=失误数/总次数，不指定时默认为0.03
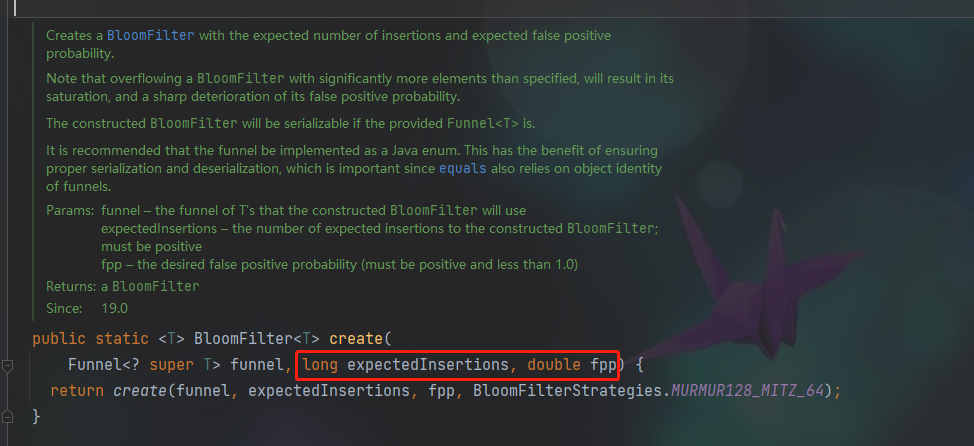
构建后，将根据expectedInsertions(参数n)和fpp(参数)p根据最优公式计算出对应的bit位(参数m)和hash算法的个数(参数k)
bit集合所需位数(参数m)和哈希函数个数(参数k)的计算方法
/**
* 计算出bit集合所需位数
* @param n 预期数据量
* @param p 失误率
* @return m bit集合位数
*/
static long optimalNumOfBits(long n, double p) {
if (p == 0) {
p = Double.MIN_VALUE;
}
return (long) (-n * Math.log(p) / (Math.log(2) * Math.log(2)));
}
/**
* 计算出hash函数所需个数
* @param n
* @param m
* @return k 哈希函数个数
*/
static int optimalNumOfHashFunctions(long n, long m) {
// (m / n) * log(2), but avoid truncation due to division!
return Math.max(1, (int) Math.round((double) m / n * Math.log(2)));
}
最后将bit位数据将转为Long数组进行存储（这一步叫做map映射）
3、测试代码
/**
* @author GGBOOM
* @description 布隆过滤器测试
* @createTime 2022/10/26 17:58
*/
public class BloomFilterTest {
/**
* 测试默认布隆过滤器失误率
* size：原始数据量 10000
* testSize：测试数据量 100000
* fpp：失误率(失误数/测试数据量),未指定时，源码默认0.03(百分之3)
* bit位数：36277*64=2321728bit约等于0.277M
* hash函数数量：5
*/
@Test
public void testBloomFilterDefault() {
// 原始数据量
int size = 10000;
BloomFilter<CharSequence> bloomFilter =
BloomFilter.create(Funnels.stringFunnel(
Charset.forName("utf-8")), size);
// 初始化数据
for (int m = 0; m < size; m++) {
bloomFilter.put("" + m);
}
List<Integer> list = new ArrayList<>();
// 测试数据
int testSize = 10000;
// 以下全为新数据，若有判断存在的，将视为一次失误添加进list
for (int n = size + testSize; n < size + 2 * testSize; n++) {
if (bloomFilter.mightContain("" + n)) {
list.add(n);
}
}
double errorRate = Double.valueOf(list.size()) / testSize;
System.out.println("误判率：" + errorRate);
// 误判率：0.0312
}
/**
* 测试指定失误率的布隆过滤器
* size：原始数据量 10000
* testSize：测试数据量 100000
* fpp：失误率(失误数/测试数据量),这里指定为0.0001
* bit位数：94669*64=6058816bit约等于0.722M
* hash函数数量：13
*/
@Test
public void testBloomFilterWithFpp() {
// 原始数据量
int size = 10000;
// 失误率
double fpp = 0.0001;
BloomFilter<CharSequence> bloomFilter =
BloomFilter.create(Funnels.stringFunnel(
Charset.forName("utf-8")), size, fpp);
// 初始化数据
for (int m = 0; m < size; m++) {
bloomFilter.put("" + m);
}
List<Integer> list = new ArrayList<>();
// 测试数据
int testSize = 10000;
// 以下全为新数据，若有判断存在的，将视为一次失误添加进list
for (int n = size + testSize; n < size + 2 * testSize; n++) {
if (bloomFilter.mightContain("" + n)) {
list.add(n);
}
}
double errorRate = Double.valueOf(list.size()) / testSize;
System.out.println("误判率：" + errorRate);
// 误判率：1.0E-4，即0.0001
}
}
七、参考
http://www.doitedu.cn/archives/2662.html
扫一扫
422
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
