Bloom Filter

查询利器-bloom-filter详解

布隆过滤器（Bloom Filter）是1970年由布隆提出的。它实际上是一个很长的二进制向量和一系列随机映射函数。布隆过滤器可以用于检索一个元素是否在一个集合中。它的优点是空间效率和查询时间都远远超过一般的算法，缺点是有一定的误识别率和删除困难。本文着重于在实现Bloom Filter的时候会使用到的一些技巧。

布隆过滤器的原理不难理解。相对于一个精简的HashMap的数据结构，存入数据的时候，不存入数据本身，只保存其Hash的值。可以用于判断该数据是否存在。其本质是用Hash对数据进行"有损压缩"的位图索引。详细参见。

 

错误率

如果用来存放Hash值的槽位足够多，那么碰撞的概率就会比较小。但是所占用的空间就会比较大。所以当分配空间的时候，需要通过你能容忍的错误率和需要存放的Key的数量来指定。如果所需存储的Key数量是n,错误率是p，所需要的槽位是m。有计算槽位的公式 m=−nlnp(ln2)2. ，也有计算概率的公式 p=(1−e−(m/nln2)n/m)(m/nln2) 。这些公式当然不是我推导出来的，想来也不太难，就不赘述推导过程了。下面这张图可以很好的表示n和m取不同的值的时候，p的值。

根据这张图。我们可以计算出所需要的内存使用量。如果把错误率控制在1%以下的话。

保存key数	占用空间
1万	64KB
10万	1MB
100万	16MB
1000万	256MB
1亿	<4GB

 

可见占用的空间在key的数量在百万级别还是很划算的，但到了上亿的级别就不那么划算了。

Bloom Filter的插入和查询都是常数级别的，所以最大的问题就是占用内存过大。而初次分配内存的时候，如果没有能够确认槽位的个数。如果分配过多会导致内存浪费，太少就会倒是错误率过高。下面提到的两个改进方案可以分别解决这两个问题。

折叠

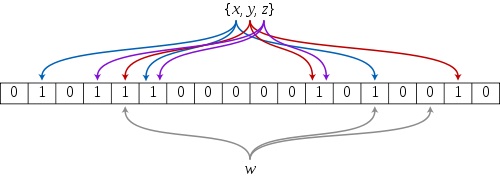
折叠是指当你初始化一个Bloom Filter的时候，可以分配足够大的槽位，等到Key导入完毕后，可以对使用的槽位进行合并操作。具体方法是将槽位切成两半，一边完全叠加到另一边上。减少内存的使用量。检查key的代码要做稍许改变。例：

 

通过这个操作，可以使实际使用的内存量减半。多执行几次，能减少更多。

动态扩展

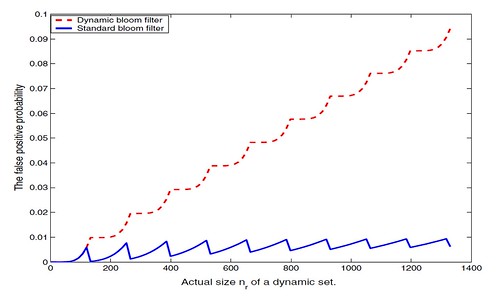
通过折叠操作，可以解决分配过大的问题，但是如果一开始分配过小，就需要扩展槽位才行。如何扩展呢？只要按原尺寸再建立一个Bloom Filter数组。原来的那个保存起来，不再写入。有新的写请求的时候，就将数据写入到新的那个Bloom Filter数组里面去。等到新的也写满了，就再建立一个，以此类推。查询的时候，就需要遍历每一个Bloom Filter数组才行。但因为查询一个Bloom Filter数组的速度很快，查询一组Bloom Filter数组也不会太影响性能。使用这种手段可以是Bloom Filter的大小可以轻易的扩展。但这样做有个的缺陷，就是错误率会随着数组的增加而上升，因为实际的数组长度并没有增加。

通过上面的两个方法，就可以解决BloomFilter的分配内存的问题。但无论哪种方法都有自己局限性，折叠每次只能减半，不是很精确。动态增加的方法会造成错误率增加。最好还是能预先估计到这个BloomFilter的容量。