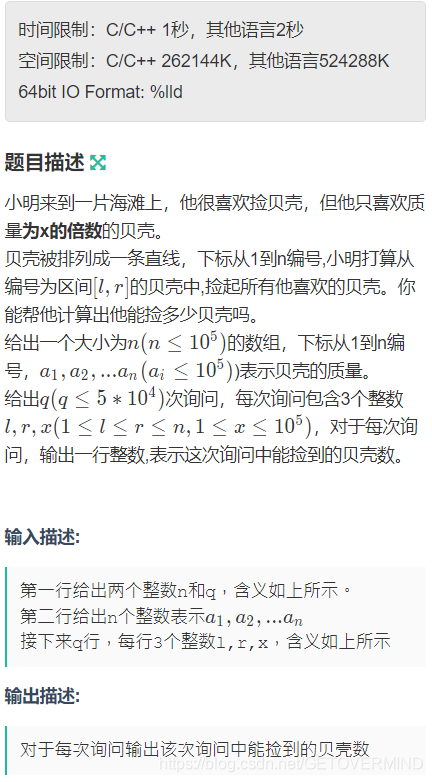
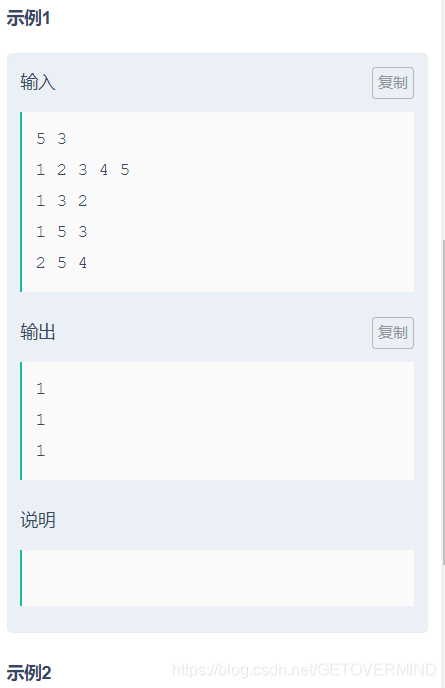
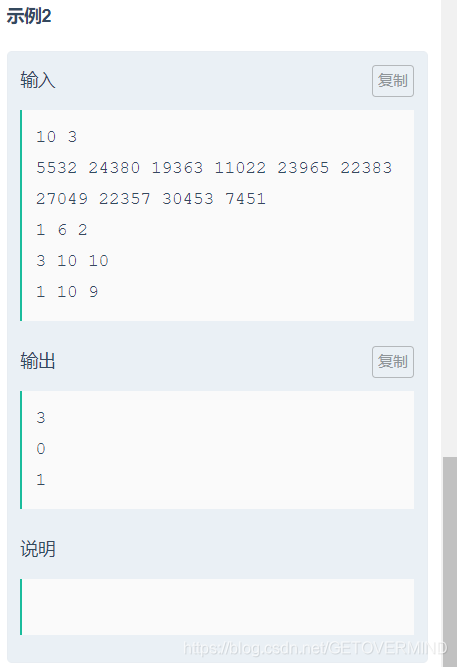
很明显这题暴力去做肯定超时,但是感觉暴力优化一下也还差不多,那么可以考虑利用分块算法来进行“优雅地暴力”,分块算法的基础应用是将一段长度为n的数据以每段根号n个数据的规模来划分成根号n块,每一块都维护一个属性,这样进行区间查询的时候,其中是整块的就把维护的属性直接加到答案上去,然后枚举那些不是整块的数据即可,分块算法的复杂度中一般是带有根号n的,乍一看感觉分块算法和线段树原理上差不多,但实际上分块算法能做到一些线段树做不到的事情,因为线段树的每一段必须满足区间可加减的性质(因为要维护整个线段树嘛),但是分块算法不需要满足这一条件,维护啥属性都行,因为它本质上还是个暴力嘛。。。
下面是代码:
#include<iostream>
#include<cmath>
using namespace std;
const int maxn = 1e5+5;
int dat[maxn];//这个数组中存放着输入的数据
int sum[350][maxn];//这个数组的第一维表示每一个块,每个块一般都是根号n的长度,因为数据范围是1e5所以开350就够了,第二维表示这一块中有多少个某个数字的倍数
int n,q;
void blocked()//分块+信息处理
{
int sz=sqrt(n);//获得每个分块的长度
for(int i=0;i<n;++i)//从0开始分块比较方便表示
{
for(int j=1;j*j<=dat[i];++j)//找j的倍数
{
if(dat[i]%j==0)//找到j的倍数
{
sum[i/sz][j]++;//让这一分块的j的倍数数量++
if(dat[i]/j!=j) sum[i/sz][dat[i]/j]++;//让这一分块的dat[i]/j的倍数数量++,!=j是因为j的倍数数量前面加过了,再加会重复
}
}
}
}
int query(int l,int r,int x)
{
int sz=sqrt(n);//获得每个分块的长度
int ans=0;
for(int i=l;i<=r&&l/sz==i/sz;++i)//遍历最左边的元素到第一个整块的起点这一段中间的数据,l/sz==i/sz说明l和i在同一块中
{
if(dat[i]%x==0) ans++;//若其中有元素是x的倍数,ans就++
}
if(l/sz==r/sz)//满足这个条件说明l到r这一段是在同一个整块中,若如此,则上面的计算结果就是最终的答案
{
return ans;
}
for(int i=r;i>=l&&i/sz==r/sz;--i)//遍历最右边的元素到第一个整块的终点这一段中间的数据,r/sz==i/sz说明r和i在同一块中
{
if(dat[i]%x==0) ans++;//若其中有元素是x的倍数,ans就++
}
for(int i=l/sz+1;i<=r/sz-1;++i)//最后统计整块的数据
{
ans+=sum[i][x];//ans加上第i块的x的倍数数量
}
return ans;
}
int main()
{
cin>>n>>q;
for(int i=0;i<n;++i)
{
cin>>dat[i];
}
blocked();//分块
int l,r,x;
for(int i=1;i<=q;++i)
{
cin>>l>>r>>x;
l--;//因为数据存储的时候编号是从0开始的
r--;
cout<<query(l,r,x)<<endl;
}
return 0;
}
/*
5 3
1 2 3 4 5
1 3 2
1 5 3
2 5 4
1
1
1
*/
/*
10 3
5532 24380 19363 11022 23965 22383 27049 22357 30453 7451
1 6 2
3 10 10
1 10 9
3
0
1
*/





 本文探讨了分块算法在处理大规模数据时如何通过优化暴力解法来提高效率。通过将数据分为根号n大小的块,分别维护每个块内的特定属性,分块算法可以在查询区间内快速获取信息,且不需满足区间操作的限制。代码示例展示了分块算法在求解数据中特定数字倍数出现次数问题的应用,复杂度中带有根号n的项。
本文探讨了分块算法在处理大规模数据时如何通过优化暴力解法来提高效率。通过将数据分为根号n大小的块,分别维护每个块内的特定属性,分块算法可以在查询区间内快速获取信息,且不需满足区间操作的限制。代码示例展示了分块算法在求解数据中特定数字倍数出现次数问题的应用,复杂度中带有根号n的项。
















 8550
8550

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








