递归入门之汉诺塔问题

递归最重要的是找出递归式之间的关系，虽然有时侯道理很容易想通，但代码不好实现，所以考虑某个问题的时候尽量画出函数的每一层调用，手动模拟一下递归。

 以汉诺塔的例子来说，设有 A， B ， C  三个圆柱， A 上有 n 个圆盘，圆盘由1~n逐渐增大，移动时大圆盘不能放在小圆盘上，

则要使 n个圆盘由   A   ---->  C  ，我们需要先移动前 n - 1 个。

而移动 前 n - 1 个我们必须移动 前 n - 2 个；

由此我们发现了汉诺塔递归函数中， 前 n - 1 个可以看做一个整体， 所以 n ---> n - 1  -----> n - 2 ---->........------> 2----->1

所以 递归的出口是 n == 1； 当 n == 1 时，也就是第一个，我们直接将其移动到 C； 

当 n == 2 时， 我们需要把第一个由A移动到 B，然后将 第二个放到 C，最后将第一个由B 移动到 C ；

当 n == 3时， 我们需要将前两个 通过 C 移动到 B；

....以此类推。

如图：

 

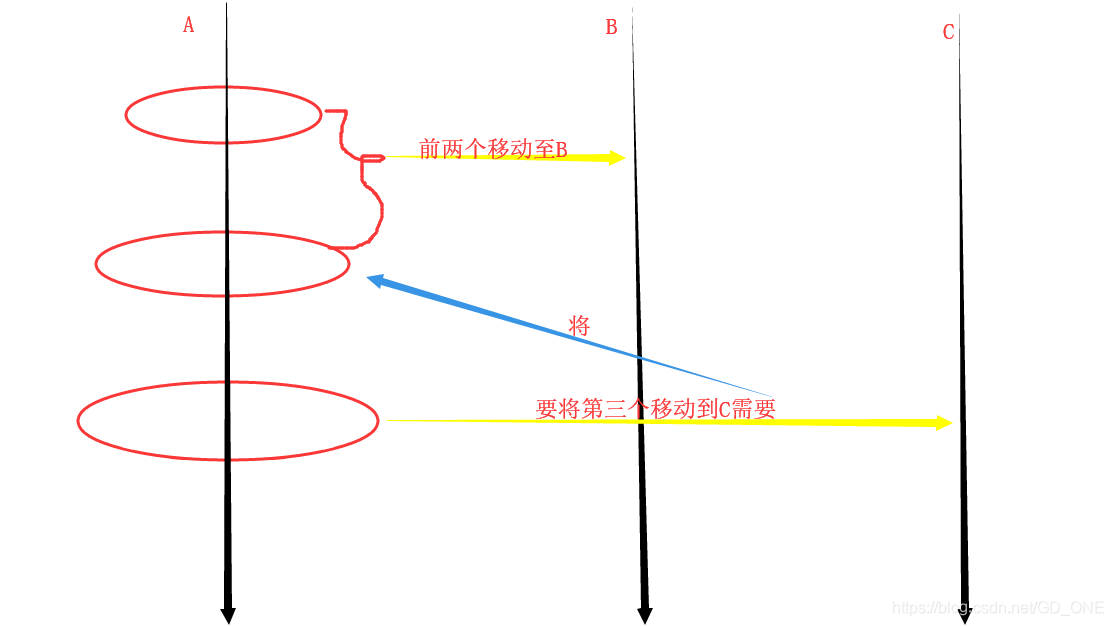
将前n-1个看作一个整体，每一次移动都需要交换b,和c的位置， 所以我们可以写出下列递归函数：

void hanno(int n, char a, char b, char c){
    if(n==1) {printf("%c-->%c",a,c);return;}// a ---> c 
    hanno(n-1, a, c, b);  // n-1 移动到 B；
    printf("%c-->%c",a,c);
    hanno(n-1,b, a, c);   // 由 B 移动到 C；
}