基础进制转换

二进制：以2为基数，由0和1表示，逢2进1.

八进制：以8为基数，由0-7这8个数字表示，逢8进1.

十进制：以10为基数，由0-9这10个数字来表示，逢10进1.

十六进制：以16为基数，由0-9以及A-F这16个数字和字母来表示，其中A-F表示10-15.

(1) 二进制转十进制

规则：从右向左用二进制的每个数去乘以2的相应次方，如果有小数的话，则小数点是从左向右。

例：1011.011（2）=1*2^0+1*2^1+0*2^2+1*2^3+0*2^-1+1*2^-2+1*2^-3=1+2+0+8+0+0.25+0.125=11.375(10)

(2)十进制转二进制

规则：除二取余法（除以2取余，最后逆序排列）

78（10）=1001110(2)

78/2=39....0

39/2=19....1

19/2=9....1

9/2=4....1

4/2=2....0

2/2=....0

1

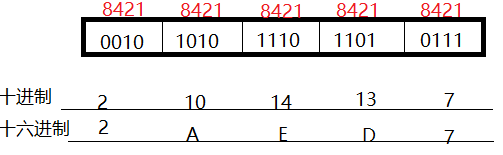
(3)二进制转十六进制

规则：8421法

101010111011010111（2）=2AED7（16）

从右向左每4位为1组，不足补0

 

(4)二进制转八进制

二进制011101.010110

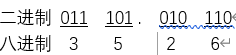
百度经验链接：https://jingyan.baidu.com/article/f96699bb7b8710c94f3c1b13.html