数据结构与算法之二叉树

前提条件

• 熟悉C语言与指针
• 熟悉数据结构与算法

概念和性质

• 二叉树（Binary tree）是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式，二叉树特点是每个结点最多只能有两棵子树，且有左右之分 。

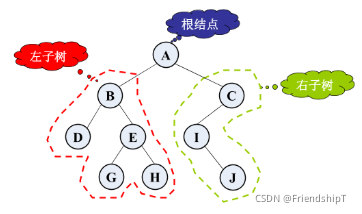
• 二叉树是n个有限元素的集合，该集合或者为空、或者由一个称为根（root）的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成，是有序树。当集合为空时，称该二叉树为空二叉树。在二叉树中，一个元素也称作一个结点。

• 如下图所示。
  

• 二叉树（Binary Tree）是含有n (n≥0）个结点( node）的有限集合。当n = 0时称为空二叉树。在非空二叉树中:

  • (1）有且仅有一个称为根(root)的结点;
  • (2〉其余结点划分为两个互不相交的子集L和R，其中L和R也是一棵二叉树，分别称为左子树( left subtree）和右子树（right subtree)，且其次序不能颠倒。(其余结点0个的话，划分为两个空集——两棵空子树)
    

• 二叉树的特点:

  • (1)二叉树可以为空树;
  • (2)二叉树中的每个结点都恰好都有两棵子树，其中一个或两个可能为空;
  • (3)二叉树中每个结点的左、右子树的位置不能颠倒。若改变两者的位置，就成为另一棵二叉树。

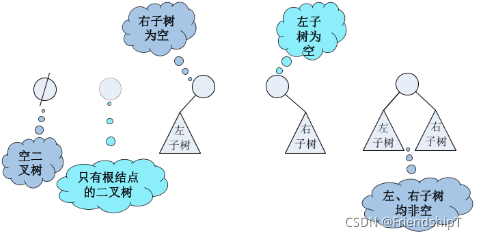
• 二叉树的5种基本形态:
  

• 二叉树的基本术语:

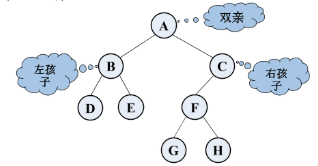
  • 二叉树的结点包含一个数据元素及指向其左右子树的两个分支，分别称为左分支和右分支。
  • 结点的左、右子树的根称为该结点的左、右孩子，统称为孩子(children)，相应地，该结点称为孩子的双亲(parent）。
    

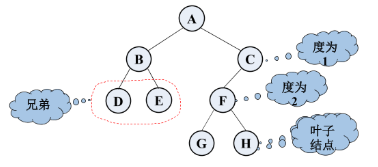
• 同一个双亲的孩子之间可互称为兄弟( sibling)。

• 结点的孩子个数称为结点的度( degree)

• 度为0的结点称为叶子结点(leaf)。

• 非叶子结点称为内部结点或分支结点（ internal node) .
  

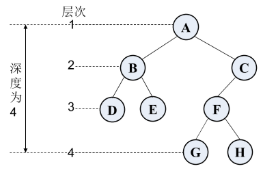
• 结点的层次（level) :从根结点开始定义，根为第1层，根的孩子为第2层，如此计数，直到该结点为止。

• 二叉树的深度(depth)或高度(height):二叉树中结点的最大层次。
  

• 二叉树的性质:

  • 性质1:在二叉树的第$i$层上至多有$2^{i-1}$个结点。$(i>=1)$
  • 性质2:深度为k的二叉树上最多含$2^k-1$个结点（k≥1)。
  • 性质3:对于任意一棵二叉树，如果度为0的结点个数为$n_0$，度为2的结点个数为$n_2$，则$n_0=n_2+1$。
  • 性质4:具有n个结点的完全二叉树的深度为$└lo{g}_{2}n┘+1$。$(注:└x┘意思是取x的下整)$
  • 性质5:对于含n个结点的完全二叉树中编号为$i(1\le i\le n)$的结点:
    • ( 1)如果i=1，则i结点是这棵完全二叉树的根，没有双亲;否则其双亲的编号为i/2。
    • (2)如果$2_i>n$，则i结点没有左孩子;否则其左孩子的编号为2i。
    • (3)如果$2_i+1>n$，则i结点没有右孩子;否则其右孩子的编号为$2_i+1$。

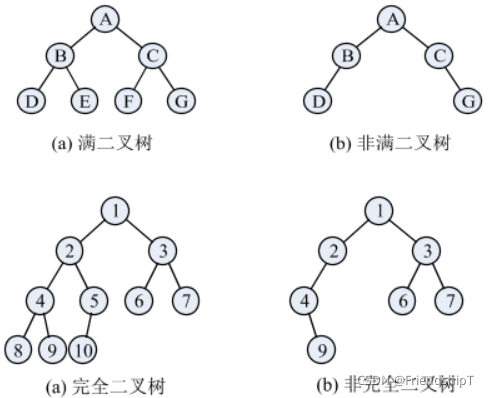
• 两类特殊二叉树:

  • 满二叉树:深度为k且含有$2^k-1$个结点的二叉树。(除最后一层外,每一层上的所有结点都有两个子结点)
  • 完全二叉树:二叉树中所含的n个结点和满二叉树中编号为1至n的结点一一对应。
    

二叉树链式存储结构

二叉树结构体(二叉链表)

• 利用顺序存储结构存储一般二叉树容易造成空间浪费,链式存储结构可以克服这个缺点。由于二叉树每个结点最多有两个孩子,所以其结点存储结构应当包括一个数据域和两个指针域:

lchild	data	rchild

• 其中, lchild和 rchild是分别指向该结点左孩子和右孩子的指针域,data是数据域。利用这种结点构建的二叉树链式存储结构称为二叉链表(Binary Linked List）,其类型定义如下:

typedef struct BiTnode
{
    char data; /*结点的数据域*/
    struct BiTnode *lchild,*rchild;/*左孩子指针域和右孩子指针域*/
}BiTnode,*BiTree;

二叉树基本操作

前序创建二叉树

void CreatBiTree(BiTree *T)
/*前序创建一棵二叉树*/
{
    char c;
    scanf("%c",&c);
    if(c == '#') /*用'#'作为子树为空的标志*/
        *T = NULL;
    else{
        *T = (BiTnode *)malloc(sizeof(BiTnode));   /*创建根结点*/
        (*T)->data = c;     /*向根结点中输入数据*/
        CreatBiTree(&((*T)->lchild));   /*递归地创建左子树*/
        CreatBiTree(&((*T)->rchild));   /*递归地创建右子树*/
    }
}

递归遍历

前序遍历算法

void preOrder(BiTree root)
/*二叉树先序遍历*/
{
    if(root==NULL) return;/*遇到空树(子树)时返回*/
    else
    {
        printf("%c",root->data);/*访问根结点*/
        preOrder(root->lchild);/*先序遍历根结点的左子树*/
        preOrder(root->rchild);/*先序遍历根结点的右子树*/
    }
}

中序遍历算法

void inOrder(BiTree root)
/*二叉树中序遍历*/
{
    if(root==NULL) return;/*遇到空树(子树)时返回*/
    else
    {
        inOrder(root->lchild);/*中序遍历根结点的左子树*/
        printf("%c",root->data);/*访问根结点*/
        inOrder(root->rchild);/*中序遍历根结点的右子树*/
    }
}

后序遍历算法

void postOrder(BiTree root)
/*二叉树后序遍历*/
{
    if(root==NULL) return;/*遇到空树(子树)时返回*/
    else
    {
        postOrder(root->lchild);/*后序遍历根结点的左子树*/
        postOrder(root->rchild);/*后序遍历根结点的右子树*/
        printf("%c",root->data);/*访问根结点*/
    }
}

完整代码

#include<stdio.h>
#include<stdlib.h>

typedef struct BiTnode
{
    char data; /*结点的数据域*/
    struct BiTnode *lchild,*rchild;/*左孩子指针域和右孩子指针域*/
}BiTnode,*BiTree;


void CreatBiTree(BiTree *T)
/*前序创建一棵二叉树*/
{
    char c;
    scanf("%c",&c);
    if(c == '#') /*用'#'作为子树为空的标志*/
        *T = NULL;
    else{
        *T = (BiTnode *)malloc(sizeof(BiTnode));   /*创建根结点*/
        (*T)->data = c;     /*向根结点中输入数据*/
        CreatBiTree(&((*T)->lchild));   /*递归地创建左子树*/
        CreatBiTree(&((*T)->rchild));   /*递归地创建右子树*/
    }
}

void preOrder(BiTree root)
/*二叉树先序遍历*/
{
    if(root==NULL) return;/*遇到空树(子树)时返回*/
    else
    {
        printf("%c",root->data);/*访问根结点*/
        preOrder(root->lchild);/*先序遍历根结点的左子树*/
        preOrder(root->rchild);/*先序遍历根结点的右子树*/
    }
}

void inOrder(BiTree root)
/*二叉树中序遍历*/
{
    if(root==NULL) return;/*遇到空树(子树)时返回*/
    else
    {
        inOrder(root->lchild);/*中序遍历根结点的左子树*/
        printf("%c",root->data);/*访问根结点*/
        inOrder(root->rchild);/*中序遍历根结点的右子树*/
    }
}

void postOrder(BiTree root)
/*二叉树后序遍历*/
{
    if(root==NULL) return;/*遇到空树(子树)时返回*/
    else
    {
        postOrder(root->lchild);/*后序遍历根结点的左子树*/
        postOrder(root->rchild);/*后序遍历根结点的右子树*/
        printf("%c",root->data);/*访问根结点*/
    }
}

int main()
{
    BiTree T = NULL;    /*最开始T指向空*/
    printf("Please Input Chars To Create A BinaryTree.\n");
    CreatBiTree(&T);    /*创建二叉树(ABD###CE#G##F##)*/
    printf("preOrder:");
    preOrder(T);/*先序遍历二叉树*/
    printf("\ninOrder:");
    inOrder(T);/*中序遍历二叉树*/
    printf("\npostOrder:");
    postOrder(T);/*后序遍历二叉树*/
    printf("\n");
    system("pause");
    return 0;
}

输出结果

[1] 严蔚敏，吴伟民. 数据结构（C语言版）. 北京： 清华大学出版社，2020
[2] 严蔚敏，李冬梅，吴伟民. 数据结构（C语言版）（第二版）. 北京： 人民邮电出版社，2021
[3] 吴伟民，李小妹，刘添添，黄剑锋，苏庆，林志毅，李杨.数据结构. 北京：高等教育出版社，2017