前提条件
- 熟悉C语言与指针
- 熟悉数据结构与算法
简介
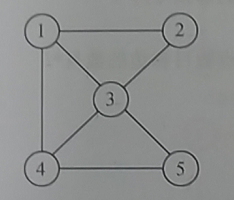
- 图(Graph)结构是一种非线性的数据结构,图在实际生活中有很多例子,比如交通运输网,地铁网络,社交网络,计算机中的状态执行(自动机)等等都可以抽象成图结构。图结构比树结构复杂的非线性结构。
- 如下图所示。
图结构体
#define MaxN 50 /*图中顶点数目最大值*/
typedef struct ArcNode
{ /*邻接链表的表结点 */
int adjvex; /*邻接顶点的编号*/
double weight;/*边(弧)上的权值*/
struct ArcNode *nextarc; /*下一个邻接顶点的结点指针*/
}EdgeNode;
typedef struct VNode
{/*邻接链表的头结点*/
char data; /*顶点表示的数据,以一个字符表示*/
struct ArcNode *firstarc;/*指向第一条依附于该顶点的弧(边)的指针*/
}AdjList[MaxN];
typedef struct
{
int Vnum,Enum;/*图中实际的顶点数目和边的数目*/
AdjList Vertices;
}Graph;
图基本操作
用邻接链表创建图
void CreateGraph(Graph *G)
/*用邻接链表创建图*/
{
int i,j,k;
EdgeNode *p;
printf("Input the number of vertex and edge:\n");
scanf("%d %d",&G->Vnum,&G->Enum); //输入顶点个数和边数
//建立邻接链表的头结点
printf("Input the data of vertex:\n"); //输入顶点信息
for(i=0;i<G->Vnum;i++){
getchar();//没有这条语句会报错,原因暂时未知
scanf("%c",&G->Vertices[i].data);
G->Vertices[i].firstarc=NULL;//初始化指向第一条依附于该顶点的弧(边)的指针
}
//建立邻接链表的表结点
printf("Input the subscript i,j of (Vi,Vj):\n");
for(k=0;k<G->Enum;k++){
scanf("%d %d",&i,&j);
p=(EdgeNode *)malloc(sizeof(EdgeNode));
p->adjvex=j; //存储弧头
p->nextarc=G->Vertices[i].firstarc; //头插法插入边结点
G->Vertices[i].firstarc=p;
//如果是创建有向图,则要删掉下面的代码
p=(EdgeNode *)malloc(sizeof(EdgeNode));
p->adjvex=i; //存储弧头
p->nextarc=G->Vertices[j].firstarc; //头插法插入边结点
G->Vertices[j].firstarc=p;
}
//输出邻接链表
printf("AdjacencyList:\n");
for(i=0;i<G->Vnum;i++){
p=G->Vertices[i].firstarc;//获取每个结点指向第一条依附于该顶点的弧(边)的指针
while(p){
printf("(%c,%c)",G->Vertices[i].data,G->Vertices[p->adjvex].data);
p=p->nextarc; //获取下一个邻接顶点的结点指针
}
printf("\n");
}
}
深度优先搜索算法
int visited[MaxN] = {0}; /*调用遍历算法前设置所有的顶点都没有被访问过*/
void Dfs(Graph G,int i)
/*以邻接链表表示图的深度优先搜索算法*/
{
EdgeNode *t;
int j;
//printf("%d",i);/*访问序号为i的顶点*/
printf("%c",G.Vertices[i].data);/*访问序号为i的顶点*/
visited[i]=1;/*序号为i的顶点已被访问过*/
t=G.Vertices[i].firstarc;/*取顶点i的第一个邻接顶点*/
while (t!=NULL)/*检查所有与顶点i相邻接的顶点*/
{
j=t->adjvex; /*顶点j为顶点i的一个邻接结点*/
if(visited[j]==0)/*若顶点j未被访问则从顶点j出发进行深度优先搜索*/
Dfs(G,j);
t=t->nextarc;/*取顶点i的一个邻接结点*/
}
}
广度优先搜索算法
void Bfs(Graph G)
/*以邻接链表表示图的广度优先搜索算法*/
{
EdgeNode *t;
SqQueue Q;
int i,j,k;
int visited[MaxN] = {0}; /*调用遍历算法前设置所有的顶点都没有被访问过*/
initQueue(&Q); /*创建一个空队列*/
for(i=0;i<G.Vnum;i++)
{
if(!visited[i])
{
enQueue(&Q,i);
//printf("%d",i);/*访问序号为i的顶点*/
printf("%c",G.Vertices[i].data);/*访问序号为i的顶点*/
visited[i]=1;/*序号为i的顶点已被访问过*/
while (!isEmpty(&Q))
{
deQueue(&Q,&k);
t =G.Vertices[k].firstarc;
for(;t;t=t->nextarc){/*检查所有与顶点k相邻接的顶点*/
j=t->adjvex;/*顶点j是顶点k的一个邻接顶点*/
if(visited[j]==0)
{
enQueue(&Q,j);
//printf("%d",j);
printf("%c",G.Vertices[j].data);
visited[j]=1;/*序号为j的顶点已被访问过*/
}
}
}
}
}
}
完整代码
#include<stdio.h>
#include<stdlib.h>
#define MAXQSIZE 100
#define MaxN 50 /*图中顶点数目最大值*/
typedef struct ArcNode
{ /*邻接链表的表结点 */
int adjvex; /*邻接顶点的编号*/
double weight;/*边(弧)上的权值*/
struct ArcNode *nextarc; /*下一个邻接顶点的结点指针*/
}EdgeNode;
typedef struct VNode
{/*邻接链表的头结点*/
char data; /*顶点表示的数据,以一个字符表示*/
struct ArcNode *firstarc;/*指向第一条依附于该顶点的弧(边)的指针*/
}AdjList[MaxN];
typedef struct
{
int Vnum,Enum;/*图中实际的顶点数目和边的数目*/
AdjList Vertices;
}Graph;
typedef struct
{
int *base; /*循环队列的存储空间首地址*/
int front,rear;/*队头、队尾指针*/
}SqQueue;
int initQueue(SqQueue *Q)
/*创建容量为MAXQSIZE的空队列*/
{
Q->base=(int *)malloc(MAXQSIZE*sizeof(int));
if(!Q->base)
return -1; //创建失败,返回-1
Q->front=0;
Q->rear=0;
return 0;
}
int isEmpty(SqQueue *Q)
/*判断队列是否为空*/
{
/*若队列为空,返回1,否则返回0*/
return Q->front==Q->rear;
}
int enQueue(SqQueue *Q,int e)
/*元素e入队*/
{/*牺牲一个元素空间,约定以"队列的尾指针所指位置的下一个位置是头指针"表示队列满*/
if((Q->rear+1)%MAXQSIZE==Q->rear)
return -1;//队列满,返回-1
Q->base[Q->rear]=e; //在当前队尾插入元素e
Q->rear=(Q->rear+1)%MAXQSIZE; //队尾指针指向下一个位置
return 0;
}
int deQueue(SqQueue *Q,int *e)
/*若队列不为空,则删除队头元素,由参数e带回其值并返回0;否则返回-1*/
{
if(Q->front==Q->rear)
return -1;//空队列,返回-1
*e=Q->base[Q->front];//获取删除队头元素的值
Q->front = (Q->front+1)%MAXQSIZE;//队头指针指向下一个位置
return 0;
}
void CreateGraph(Graph *G)
/*用邻接链表创建图*/
{
int i,j,k;
EdgeNode *p;
printf("Input the number of vertex and edge:\n");
scanf("%d %d",&G->Vnum,&G->Enum); //输入顶点个数和边数
//建立邻接链表的头结点
printf("Input the data of vertex:\n"); //输入顶点信息
for(i=0;i<G->Vnum;i++){
getchar();//没有这条语句会报错,原因暂时未知
scanf("%c",&G->Vertices[i].data);
G->Vertices[i].firstarc=NULL;//初始化指向第一条依附于该顶点的弧(边)的指针
}
//建立邻接链表的表结点
printf("Input the subscript i,j of (Vi,Vj):\n");
for(k=0;k<G->Enum;k++){
scanf("%d %d",&i,&j);
p=(EdgeNode *)malloc(sizeof(EdgeNode));
p->adjvex=j; //存储弧头
p->nextarc=G->Vertices[i].firstarc; //头插法插入边结点
G->Vertices[i].firstarc=p;
//如果是创建有向图,则要删掉下面的代码
p=(EdgeNode *)malloc(sizeof(EdgeNode));
p->adjvex=i; //存储弧头
p->nextarc=G->Vertices[j].firstarc; //头插法插入边结点
G->Vertices[j].firstarc=p;
}
//输出邻接链表
printf("AdjacencyList:\n");
for(i=0;i<G->Vnum;i++){
p=G->Vertices[i].firstarc;//获取每个结点指向第一条依附于该顶点的弧(边)的指针
while(p){
printf("(%c,%c)",G->Vertices[i].data,G->Vertices[p->adjvex].data);
p=p->nextarc; //获取下一个邻接顶点的结点指针
}
printf("\n");
}
}
int visited[MaxN] = {0}; /*调用遍历算法前设置所有的顶点都没有被访问过*/
void Dfs(Graph G,int i)
/*以邻接链表表示图的深度优先搜索算法*/
{
EdgeNode *t;
int j;
//printf("%d",i);/*访问序号为i的顶点*/
printf("%c",G.Vertices[i].data);/*访问序号为i的顶点*/
visited[i]=1;/*序号为i的顶点已被访问过*/
t=G.Vertices[i].firstarc;/*取顶点i的第一个邻接顶点*/
while (t!=NULL)/*检查所有与顶点i相邻接的顶点*/
{
j=t->adjvex; /*顶点j为顶点i的一个邻接结点*/
if(visited[j]==0)/*若顶点j未被访问则从顶点j出发进行深度优先搜索*/
Dfs(G,j);
t=t->nextarc;/*取顶点i的一个邻接结点*/
}
}
void Bfs(Graph G)
/*以邻接链表表示图的广度优先搜索算法*/
{
EdgeNode *t;
SqQueue Q;
int i,j,k;
int visited[MaxN] = {0}; /*调用遍历算法前设置所有的顶点都没有被访问过*/
initQueue(&Q); /*创建一个空队列*/
for(i=0;i<G.Vnum;i++)
{
if(!visited[i])
{
enQueue(&Q,i);
//printf("%d",i);/*访问序号为i的顶点*/
printf("%c",G.Vertices[i].data);/*访问序号为i的顶点*/
visited[i]=1;/*序号为i的顶点已被访问过*/
while (!isEmpty(&Q))
{
deQueue(&Q,&k);
t =G.Vertices[k].firstarc;
for(;t;t=t->nextarc){/*检查所有与顶点k相邻接的顶点*/
j=t->adjvex;/*顶点j是顶点k的一个邻接顶点*/
if(visited[j]==0)
{
enQueue(&Q,j);
//printf("%d",j);
printf("%c",G.Vertices[j].data);
visited[j]=1;/*序号为j的顶点已被访问过*/
}
}
}
}
}
}
int main(){
Graph G;
CreateGraph(&G); //用邻接表创建图
printf("the result of Dfs:\n");
Dfs(G,0);//图的深度优先搜索算法
printf("\nthe result of Bfs:\n");
Bfs(G);//图的广度优先搜索算法
printf("\n");
system("pause");
return 0;
}
/*
Input the number of vertex and edge:
5 7
Input the data of vertex:
1 2 3 4 5
Input the subscript i,j of (Vi,Vj):
0 3
0 2
0 1
1 2
2 3
2 4
3 4
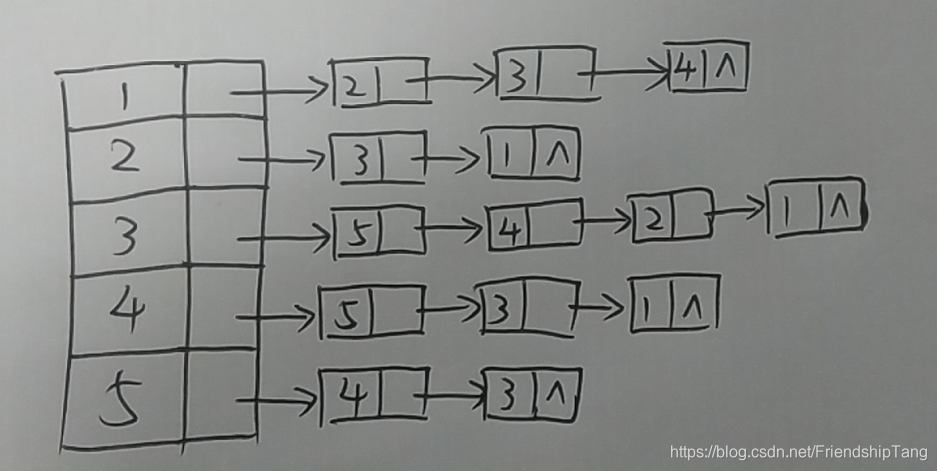
AdjacencyList:
(1,2)(1,3)(1,4)
(2,3)(2,1)
(3,5)(3,4)(3,2)(3,1)
(4,5)(4,3)(4,1)
(5,4)(5,3)
the result of Dfs:
12354
the result of Bfs:
12345
请按任意键继续. . .
*/
输出结果
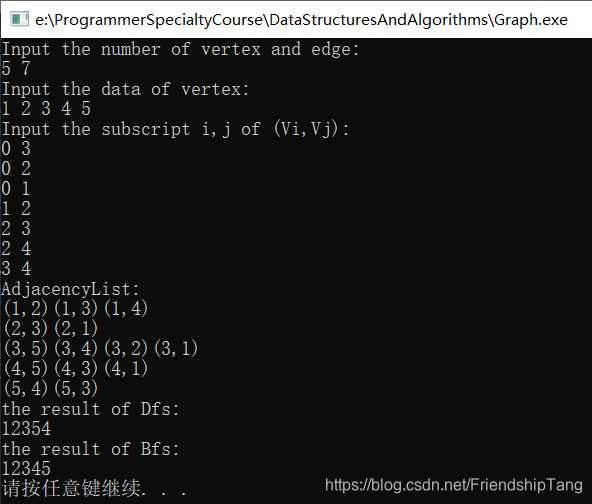























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










