Lecture 6 Language Models and Recurrent Neural Networks

这一讲的主要内容包括如何从前面所讲的经典语言模型过渡到现在的神经网络语言模型，而神经语言模型主要介绍循环神经网络（Recurrent Neural Networks,RNNs）。

如何理解语言模型（Language Model）呢？这里可以简单的将其看作是根据前面已有的句子部分来预测下一个词是什么。例如当前已有“the students opened their”，那么根据训练语料库，模型给出的预测可能是books、laptops、exams或minds等其中的一个。

如果将已有的句子表示为词的序列$x^{(1)},x^{(2)},...,x^{(t)}$，那么后一个词的预测可以看做是一种条件概率的计算$P(x^{(t+1)}|x^{(1)},x^{(2)},...,x^{(t)})$，其中所预测的$x^{(t+1)}$可能是词汇表$V=\left\{{\mathbf{w}}_1,\dots ,{\mathbf{w}}_{|V|}\right\}$中的任意一词，我们将完成这类任务的系统称为语言模型。

同样语言模型也可以为一段文本计算其出现的概率，例如我们想预测文本$x^{(1)},x^{(2)},...,x^{(T)}$出现的可能性，那么可以计算$$\begin{array}{rl}P\left({\mathbf{x}}^{(1)},\dots ,{\mathbf{x}}^{(T)}\right)& =P\left({\mathbf{x}}^{(1)}\right)\times P\left({\mathbf{x}}^{(2)}|{\mathbf{x}}^{(1)}\right)\times \cdots \times P\left({\mathbf{x}}^{(T)}|{\mathbf{x}}^{(T-1)},\dots ,{\mathbf{x}}^{(1)}\right)\\ & =\prod _{t=1}^{T}P\left({\mathbf{x}}^{(t)}|{\mathbf{x}}^{(t-1)},\dots ,{\mathbf{x}}^{(1)}\right)\end{array}$$
从中可以看出它仍是一系列条件概率的乘积，根据已有的部分预测下一个词。

其实语言模型在生活中已经有了很普遍的应用，例如输入法的联想提示，搜索引擎的自动补全等等。

语言模型中最经典的一种便是n-gram，其中n-gram表示文本中$n$个连续的词，常见的有如下的类型：

n表示我们所关注的窗口的大小，例如之前的例句：the students opened their __，对于unigrams来说需要根据前一个词预测后一个词；对于bigrams来说，需要根据连续的两个词来预测下一个词，n为其他数值时道理类似。

那么如何构造n-gram语言模型呢？一种直观的思路便是统计不同的n-gram同时出现的频率，然后利用在大语料库中得到的词共现统计信息来预测下一个最有可能出现的词。因此，假设 $x^{(t+1)}$仅依赖于前面的$n-1$个词，表示如下：

那如何得到上述的概率值呢？一种方法便是在一些很大的语料库中(n-1)-gram出现的次数和n-gram出现的次数，根据大数定律，使用频率来逼近概率。

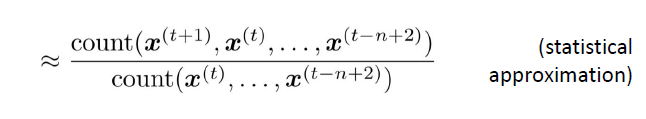
如果$n=4$，对于下句而言预测横线中的词时，我们只需要考虑students opened theair，而之前的部分由于不在窗口范围内可以舍弃不考虑。因此，根据前面的分析，条件概率计算如下所示：

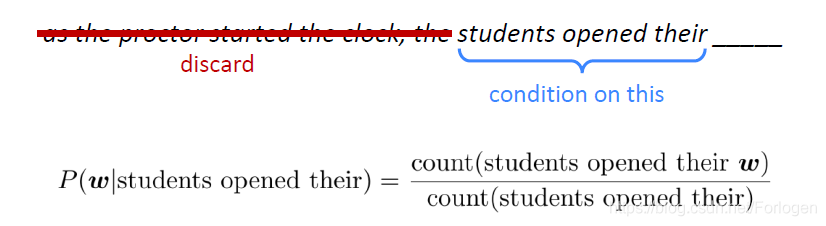
而且根据之前在语料库上的训练可知，students opened their books出现了400次，而students opened their exams出现了100次，对应的概率为0.4和0.1，那么按照出现概率的大小，后面应该接的是book。

但是这样的做法真的好吗？回想一下，因为n这里设置为了4，那么之前的很多词我们并没有考虑到，因此可能已经丢失了大量相关的上下文信息。而且从人的角度分析，当我们考虑到前面出现的部分，显然exams比books更适合此时的情况，这于根据计算得到的结果相反。

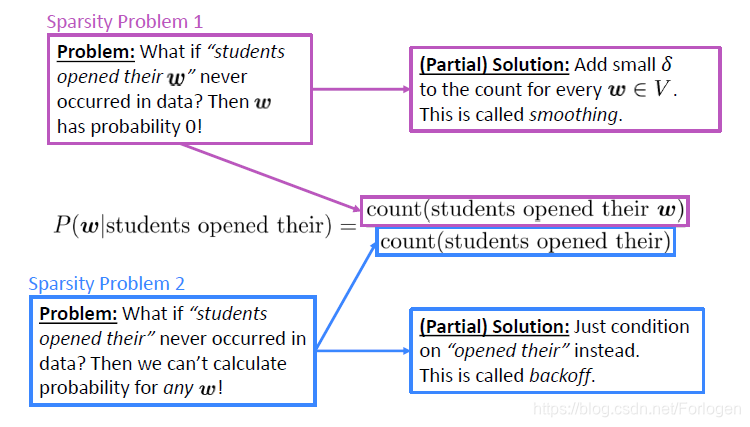
因此，n-gram语言模型一个突出的问题便是稀疏性问题（sparsity problems）。从前面概率计算的公式分析，可将稀疏性问题分为两个角度来理解：

• 对于分子部分来说，如果students opened their $w$从来都没有在训练的语料库中出现，那么对于任意的词来说，所计算的概率都是0
• 对于分母部分来说，如果students opened their就从来没在训练语料库中出现，那么预测$w$就更无从谈起了

对于第一个问题的解决方法称为smoothing，即为词汇表中的每个词都分配一个很小的$\delta$，保证概率值不会为零。对于第二个问题的解决办法是缩小考虑的范围，例如只考虑opened their，即缩小窗口的大小，这称之为back off。

而且需要注意的是，当n的值越大时，上述的问题就越严重。因此在实际应用中，n的值一般都不会超过5。除了上述的稀疏性问题，另一个严重的问题便是资源的消耗。当训练所使用的语料库很大时，需要存储的词共现信息所使用的内存资源就很大，同样的语料库越大，问题越严重。

n-gram模型一个应用便是用来生成文本，逐步的根据前面的n个词来生成后一个词

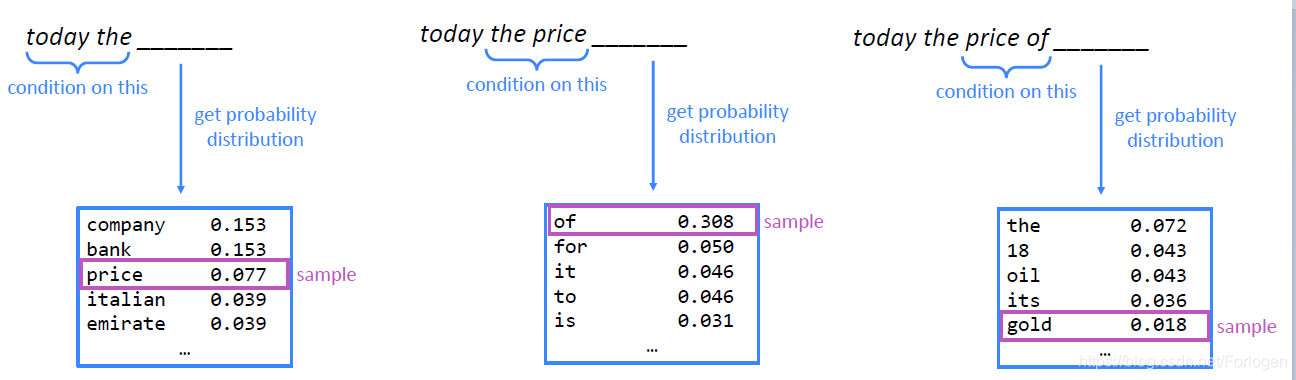
完整的生成文本的示例，可以看出还是不错的，虽然存在一定程度上的不一致性。但是如果增大n应该可以获得更好效果的文本，但同时又不得不面对前面所说的稀疏性和存储资源消耗等问题。

既然n-gram模型存在着很多的问题，有没有好的解决办法呢？一种思路便是使用神经网络语言模型，同样的需要根据已有的词的序列${\mathbf{x}}^{(1)},{\mathbf{x}}^{(2)},\dots ,{\mathbf{x}}^{(t)}$来计算$P\left({\mathbf{x}}^{(t+1)}|{\mathbf{x}}^{(t)},\dots ,{\mathbf{x}}^{(1)}\right)$。

对于基于窗口的神经语言模型来说，例如在下面的命名实体识别任务中，模型需要根据museums in Pairs are amazing识别出Pairs这里所指为Location。

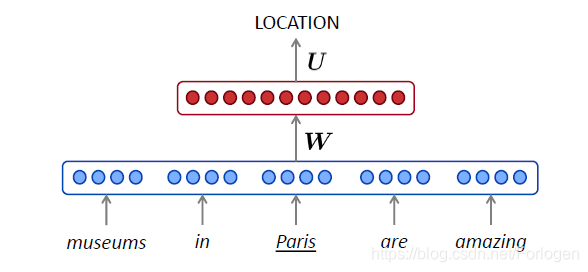
对于开始的那个例子可以表示为如下的形式，将输入词$x^{(i)}$表示为one-hot向量，然后再将其拼接为词嵌入向量$e$，然后将经过非线性转换后的结果送到Softmax层中计算下一个词出现的概率。

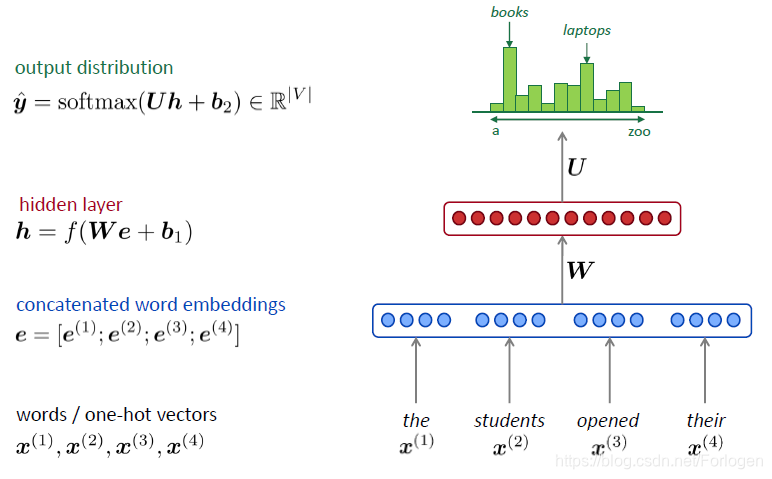
这样基于窗口的神经语言模型具有如下的优点：

• 没有稀疏性问题
• 不必存储已观察到的n-grams

但是仍存在一系列其他的问题，例如：

• 固定的窗口太小
• 如果扩大窗口的大小，权值矩阵$W$的大小也随之增大
• 考虑到实际的计算，窗口大小并不能无限的增大
• 对于$x^{(1)}$和$x^{(2)}$所使用的$W$是不同的

因此我们需要一个可以处理任意长度序列的网络架构，这便引出了RNN。一个按时间步展开的标准RNN如下所示：

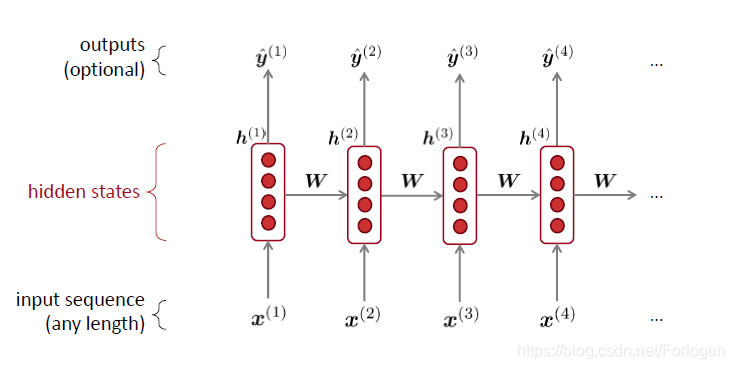
将其应用到前面的例子中，如下所示，在预测每一个词时，不仅依赖于当前的输入，同时还依赖于上一时刻的状态

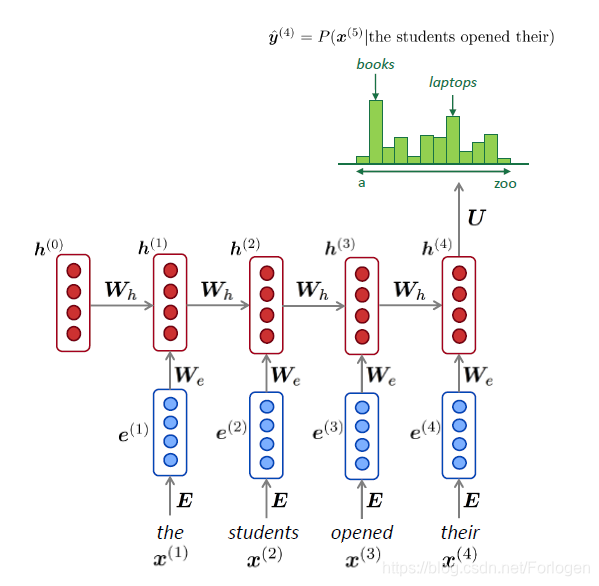
RNN具有如下的优点：

• 可以处理任意长度的输入序列
• 每一时间步的计算可以使用之前很多步的信息
• 模型的容量并不会随着输入序列长度的增加而增大
• 在所有时间步使用的是同一个权值矩阵$W$

但是RNN同样存在着一些问题：

• 计算很慢
• 难以很好的捕捉长程依赖信息

那么如何训练一个RNN语言模型，可以分为如下的几步：

• 找到一个包含词序列$x^{(1)},...,x^{(T)}$的大语料库
• 将其送到RNN-LM中，计算每个时间步输出$\widehat{y^{(t)}}$的分布，即根据已有的序列计算每个词可能的概率分布
• 计算每个时间步预测的概率分布$\widehat{y^{(t)}}$和真实分布$y^{(t)}$之间的交叉熵损失，作为模型训练的损失函数，如下所示$$J^{(t)}(\theta )=CE\left({\mathbf{y}}^{(t)},{\hat{\mathbf{y}}}^{(t)}\right)=-\sum _{w\in V}{\mathbf{y}}_w^{(t)}\log {\hat{\mathbf{y}}}_w^{(t)}=-\log {\hat{\mathbf{y}}}_{{\mathbf{x}}_{t+1}}^{(t)}$$
• 计算整个训练集上的平均损失$$J(\theta )=\frac{1}{T}\sum _{t=1}^T{J}^{(t)}(\theta )=\frac{1}{T}\sum _{t=1}^T-\log {\hat{y}}_{x_{t+1}}^{(t)}$$

对于the students opened their exams的示例可以表示为

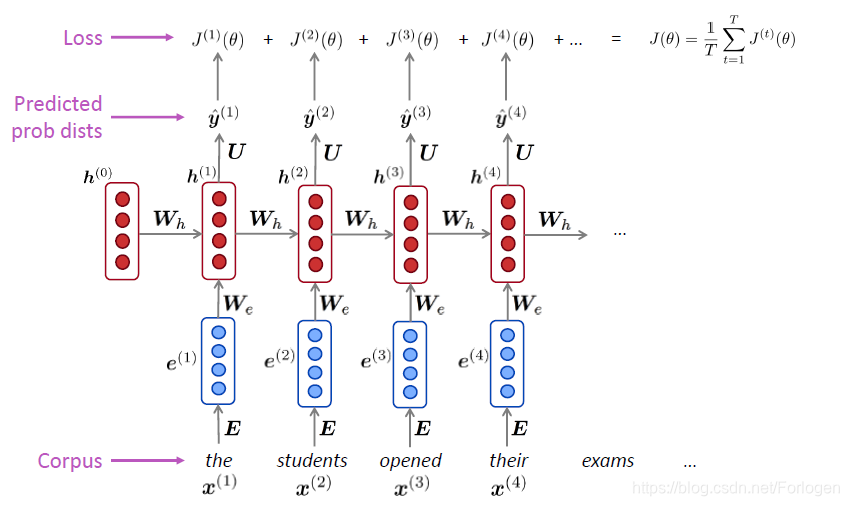
但是在整个语料库上计算损失项和梯度消耗是十分巨大的，根据批梯度下降的思想，我们可以将一个句子或文档作为输入对象，而不只是单个的词。

RNN的反向传播过程：

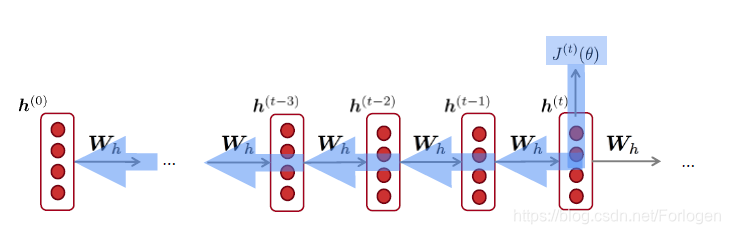
更多可见：CS224n笔记8 RNN和语言模型

对于语言模型一种标准的评估指标为perplexity，它的定义如下

它等同于交叉熵损失$J(\theta )$的指数：

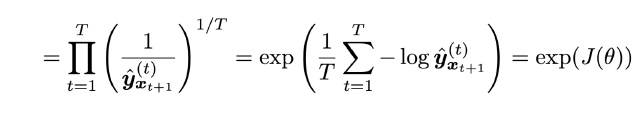
而perplexity越小，表示模型越好。通过实验可以看出RNN可以减小perplexity的值。

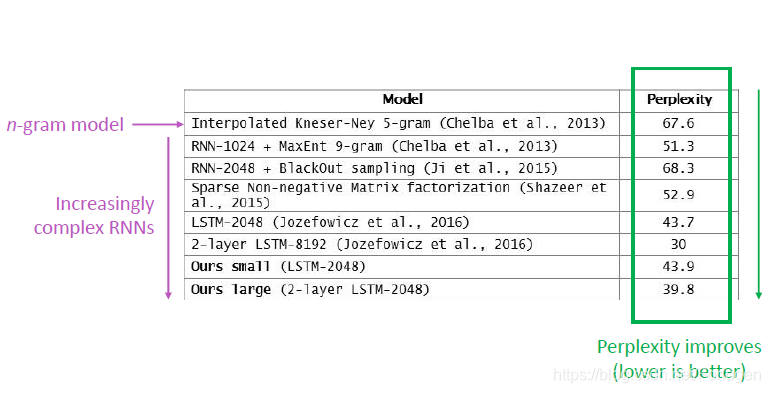
RNN的应用：

• 标注
  
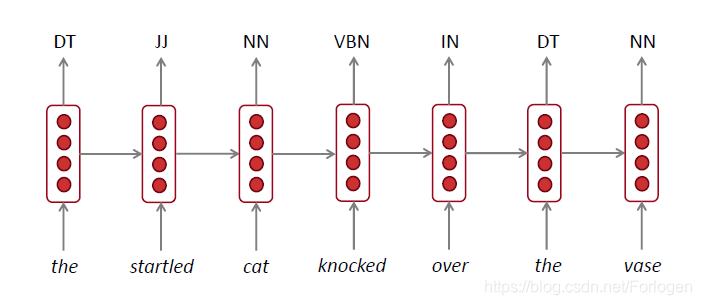
• 情感分析
  
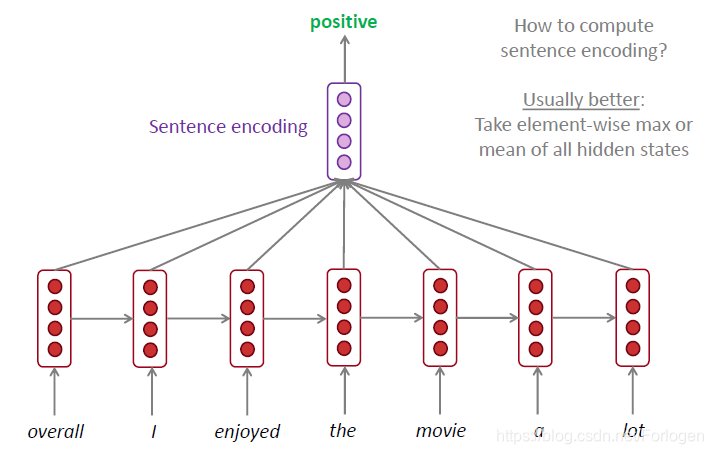
• 用于编码器，例如用于QA问题
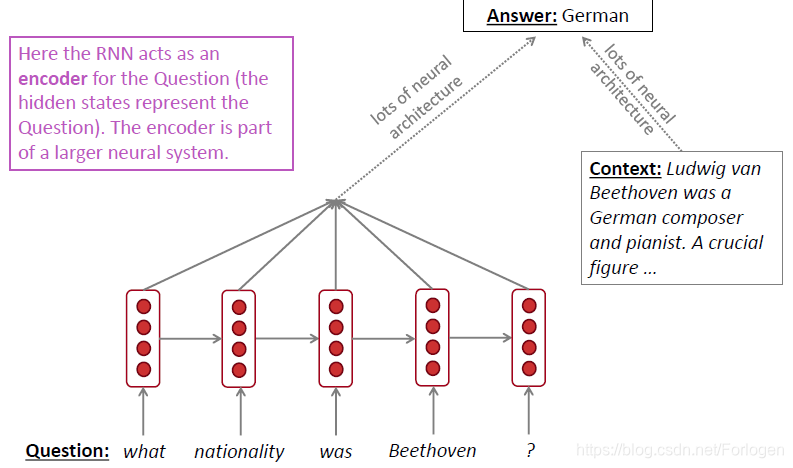
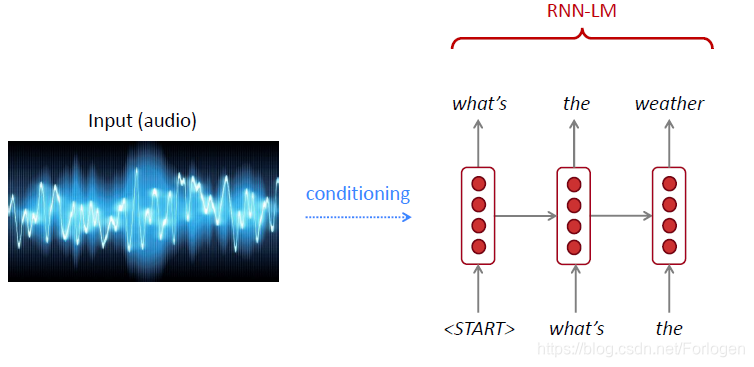
• 生成文本，例如机器翻译、语音识别、自动摘要生成等
  

总结

但在RNN的实际应用中会遇到梯度消失和梯度爆炸的问题，导致模型极其的难以训练，因此通常使用的是它的变体LSTM和GRU，以及最近所提出的Transformer，这些内容在后面的课程会继续讲解。