Inferring Semantic Layout for Hierarchical Text-to-Image Synthesis

CVPR 2018 《Inferring Semantic Layout for Hierarchical Text-to-Image Synthesis》

本文完成的也是Text-to-Image的工作，但是如果直接完成输入文本空间到生成图像像素空间的映射，由于数据的高维性，将很难找到合适的映射方式。因此作者在text-to-piexl中间加了几步，将整个任务分解为多个子任务多步进行。

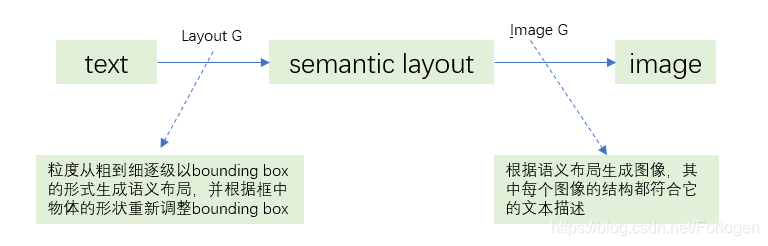
这样的生成方式具有如下的优点：

• 生成在语义上更有意义的图像
• 通过修改生成的场景布局，允许标注生成的图像、用户控制生成的过程
• 实现生成匹配复杂文本描述的复杂图像

具体的效果如下所示：用户输入“People riding on elephants that are walking through a river.”后，首先根据文本针对每个实体生成bounding box，然后根据具体的形状调整bounding box的细节部分，生成binary mask，最后根据语义布局生成最后的图像。

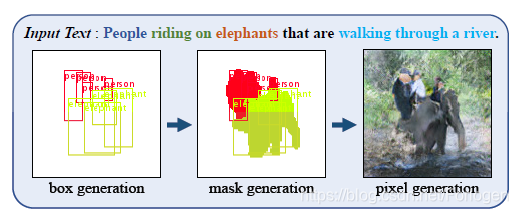
作者通过在MS-COCO数据集上进行实验，证明了提出的模型不仅可以提高生成图像的质量，同时也可以生成更符合语义描述的图像。

模型的整体架构如下所示：

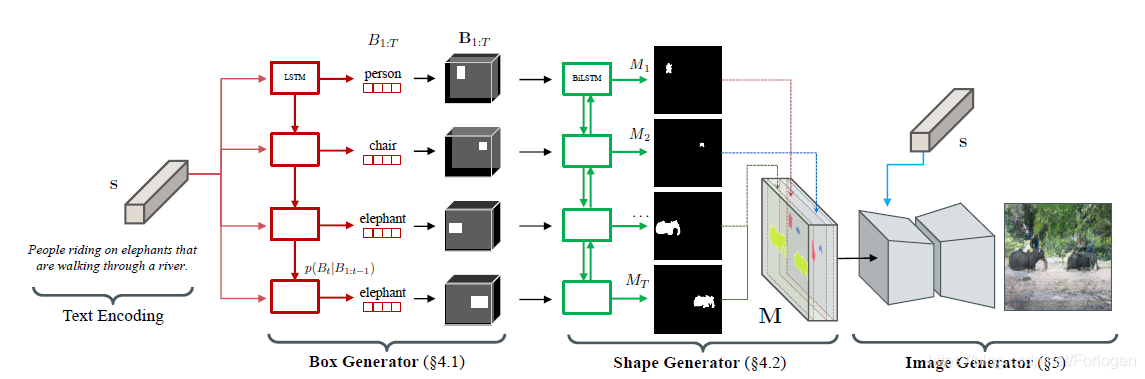
按照图像的生成过程，模型主要包括：

• Text encoding：将输入文本转换为嵌入向量的形式，作为下一阶段Box generator的输入
• Box generator：根据文本向量生成相对粗粒度的布局，输出为bounding bod的集合 B 1 : T = { B 1 , … , B T } B_{1 : T}=\left\{B_{1}, \dots, B_{T}\right\} B1:T​={B1​,…,BT​}，其中$B_t$表示第$t$个实体的位置、形状和类别
• Shape generator：根据上一阶段bounding box的集合预测框中实体的形状，输入二值掩码（binary mask）的集合 M 1 : T = { M 1 , … , M T } M_{1 : T}=\left\{M_{1}, \ldots, M_{T}\right\} M1:T​={M1​,…,MT​}，其中$M_t$定义了第$t$个实体的前景形状
• Image generator：聚合实体掩码和文本嵌入作为输入，通过将语义布局转换为匹配文本描述的像素来生成图像

这样通过将图像生成过程限制在前面得到的语义布局上，使得模型可以生成具有详细形状的实体，更容易识别其中的语义内容。下面分别来看一下每一部分的实现原理。

---

Bounding Box Generation

为了将bounding box和图像中具体的实体对应起来，这里在$B_t$中加了实体的类别标签，记为$B_t=(b_t,l_t)$，其中$b_t=\left[b_{t,x},b_{t,y},b_{t,w},b_{t,h}\right]\in {\mathbb{R}}^4$表示框的位置和大小，整个框的范围可通过坐标$(x,y)$和宽$w$和高$h$计算而得。 l t ∈ { 0 , 1 } L + 1 l_{t} \in\{0,1\}^{L+1} lt​∈{0,1}L+1是one-hot向量，表示$L$个类别实体，$L+1$作为终止的标志，即当向量的$L+1$维上取值为1时，表示已生成图中所有实体的bounding box。

因此使用自回归解码器的框生成器（box generator）将实现输入文本$s$到实体框的集合 B 1 : T = { B 1 , … , B T } B_{1 : T}=\left\{B_{1}, \dots, B_{T}\right\} B1:T​={B1​,…,BT​}的随机映射，记为${\hat{B}}_{1:T}\sim G_{\mathrm{b}\mathrm{o}\mathrm{x}}(\mathrm{s})$。直接完成$s$到$B_{1:T}$的映射难度较大，因此这里在计算联合概率$p\left(B_{1:T}|\mathbf{s}\right)$时将其分解为多个条件概率的乘积，即每一个框的生成都受前面已经生成的框的影响，具体表示为$$p\left(B_{1:T}|\mathbf{s}\right)=\prod _{t=1}^{T}p\left(B_t|B_{1:t-1},\mathbf{s}\right)$$而这样的生成流程和LSTM的过程很相似，因此作者这里也是使用了LSTM来计算右侧的条件概率。在实际的生成过程中，往往是先由实体得到类标签$l_t$，然后根据$l_t$得到$b_t$，最后根据$B_t=(b_t,l_t)$和上式计算得到最后的联合概率$p\left(B_{1:T}|\mathbf{s}\right)$。这个过程可简单的表示为$$p\left(B_t|\cdot \right)=p\left({\mathbf{b}}_t,l_t|\cdot \right)=p\left({\mathbf{l}}_t|\cdot \right)p\left({\mathbf{b}}_t|{\mathbf{l}}_t,\cdot \right)$$

这样又将一个条件概率的计算分解为两个条件概率的计算，而作者这里又使用了高斯混合模型（GMM）对其进行建模：$$\begin{array}{rl}p\left(l_t|B_{1:t-1},\mathbf{s}\right)& =\mathrm{Softmax}\left({\mathbf{e}}_t\right)\\ p\left({\mathbf{b}}_t|l_t,B_{1:t-1},\mathbf{s}\right)& =\sum _{k=1}^K{\pi }_{t,k}\mathcal{N}\left({\mathbf{b}}_t;{\mathbf{\mu }}_{t,k},{\mathbf{\Sigma }}_{t,k}\right)\end{array}$$其中上式中的参数$e_t、{\pi }_{t,k}、{\mu }_{t,k}、{\Sigma }_{t,k}$都是由LSTM在每个时间步$t$学习得到的。具体可表示为$$\begin{array}{rl}\left[h_t,c_t\right]& =\mathrm{LSTM}\left(B_{t-1};\left[h_{t-1},c_{t-1}\right]\right)\\ l_t& =W^l{h}_t+{\mathbf{b}}^l\\ {\mathbf{\theta }}_t^{xy}& =W^{xy}\left[h_t,l_t\right]+{\mathbf{b}}^{xy}\\ {\mathbf{\theta }}_t^{wh}& =W^{wh}\left[h_t,l_t,b_x,b_y\right]+{\mathbf{b}}^{wh}\end{array}$$其中${\theta }_t=\left[{\mathbf{\pi }}_{t,1:K}^{\cdot },{\mathbf{\mu }}_{t,1:K}^{\ast },{\mathbf{\Sigma }}_{t,1:K}\right]$就是包含所需参数的向量。

作者为了减少计算的难度，在计算$p(b_t|l_t\cdot )$是并不是直接计算得到$b_t=\left[b_{t,x},b_{t,y},b_{t,w},b_{t,h}\right]$，而也是分为两部进行$$\begin{array}{rl}p\left(b_t^x,b_t^y|l_t\right)& =\sum _{k=1}^K{\pi }_{t,k}^{xy}\mathcal{N}\left(b_t^x,b_t^y;{\mathbf{\mu }}_{t,k}^{xy},{\mathbf{\Sigma }}_{t,k}^{xy}\right)\\ p\left(b_t^w,b_t^h|b_t^x,b_t^y,l_t\right)& =\sum _{i=k}^K{\mathbf{\pi }}_{t,k}^{wh}\mathcal{N}\left(b_t^w,b_t^h;{\mathbf{\mu }}_{t,k}^{wh},{\mathbf{\Sigma }}_{t,k}^{wh}\right)\end{array}$$

这一阶段训练过程的目标函数如下所示，即最大化根据类标签生成接近真实情况的框的概率$$\min {\mathcal{L}}_{\mathrm{b}\mathrm{o}\mathrm{x}}=-{\lambda }_l\frac{1}{T}\sum _{t=1}^T{l}_t^{\ast }\log p\left(l_t\right)-{\lambda }_b\frac{1}{T}\sum _{t=1}^T\log p\left({\mathbf{b}}_t^{\ast }\right)$$

其中$T$表示实体的个数；${\lambda }_l=4$和${\lambda }_b=1$是超参数，$b_t^{\ast }$和$l_t^{\ast }$是第$t$个实体真实的坐标和类标签。

---

Shape Generation

在前一阶段已经得到了图中所有实体的bounding box，但是它们都是一些矩形的框，并不能准确的表示出框中物体的形状，进而准确的表示框中实体。因此这一阶段实现以二值掩码的形式$M_t\in {\mathbb{R}}^{H\times W}$预测框中实体具体的形状，实现下面的过程$${\hat{M}}_{1:T}=G_{\mathrm{m}\mathrm{a}\mathrm{s}\mathrm{k}}\left({\mathbf{B}}_{1:T},{\mathbf{z}}_{1:T}\right)$$
这里$B_{1:T}$已经变成了取值只为0或1的二值形式，$z$是采样自高斯分布$\mathcal{N}(0,I)$的随机噪声。那么一个好的$M_t$应满足以下的两个要求：

• $M_t$应该匹配$B_t$所表示的实体的位置和类别信息，且只能表示一个独立实体
• 预测的形状应符合文本的描述

这一部分的模型架构如下所示：

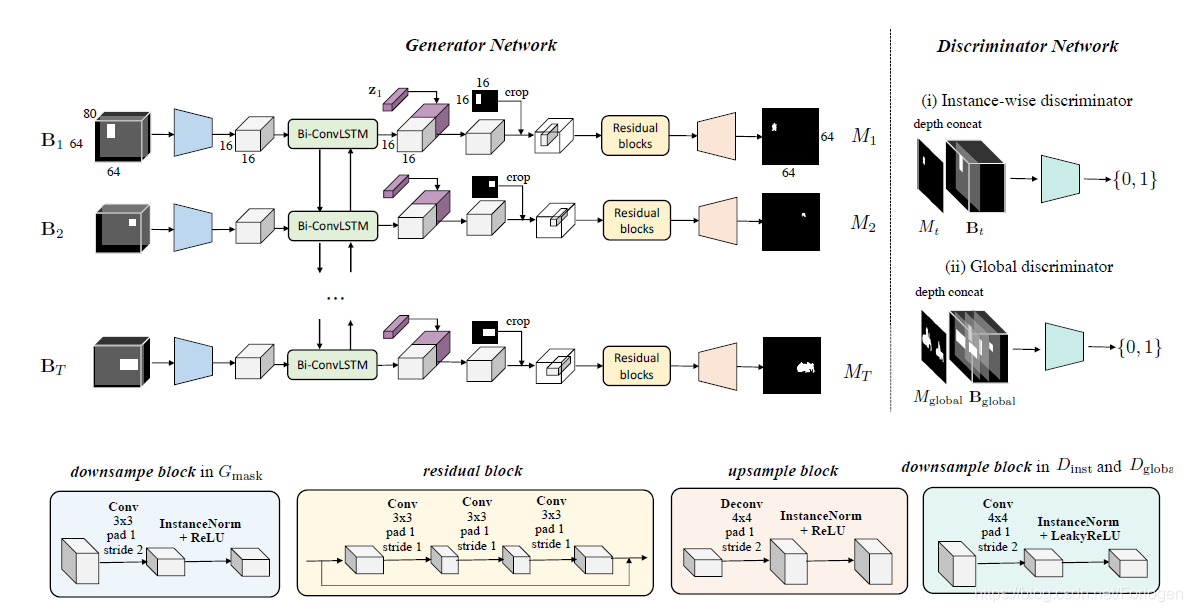
这个模型是一个卷积循环神经网络。具体的流程为：

• 每个 $B_t$ 经过两个步长为2、填充为1、卷积核大小为$3\times 3$的下采样块，接着做Instance Normalization（对单个layer的所有像素求均值和标准差），经过RELU层最终得到编码的T个 $16\times 16\times d$的特征图。
• T个map作为每一个双向 CONV-LSTM的输入。在每一个LSTM输出的前段增加随机向量$z_i$。然后经过一层卷积后，按照之前将分离的$B_t$转化为一个张量的形式，它是将box框内的值保留，box外的值置为0
• 然后通过残差块，接着进行上采样得到一个mask

最后使用判别器判断生成MASK是否符合我们前面提到的两个要求

• 为了满足第一个条件，这里使用instance-wise的D，将每一步得到的$B_t$ 和与之对应的$M_t$ ,在通道方向进行深度相连，然后D判定是否正确。
  目标函数为：$$\begin{array}{rl}{\mathcal{L}}_{\text{ inst }}^{(t)}=& {\mathbb{E}}_{\left({\mathbf{B}}_t,M_t\right)}\left[\log D_{\text{ inst }}\left({\mathbf{B}}_t,M_t\right)\right]\\ & +{\mathbb{E}}_{{\mathbf{B}}_t,{\mathbf{z}}_t}\left[\log \left(1-D_{\text{ inst }}\left({\mathbf{B}}_t,G_{\text{ mask }}^{(t)}\left({\mathbf{B}}_{1:T},{\mathbf{z}}_{1:T}\right)\right)\right)\right]\end{array}$$然后对所有实体的结果求平均

• 为了满足第二个条件，这里使用Global D。将输入变为所有的mask连接所有的$B_t$，同样下采样后，D判别生成是否合理。
  因为图像中不同实体之间不是独立存在的，它们彼此之间存在着一些联系，因此这里将所有实体的mask聚合成一个全局的mask$G_{\text{ global }}\left({\mathbf{B}}_{1:T},{\mathbf{z}}_{1:T}\right)={\sum }_t{G}_{\text{ mask }}^{(t)}\left({\mathbf{B}}_{1:t},{\mathbf{z}}_{1:t}\right)$，那么目标函数为$$\begin{array}{l}{\mathcal{L}}_{\text{ global }}={\mathbb{E}}_{\left({\mathbf{B}}_{1:T},M_{1:T}\right)}\left[\log D_{\text{ global }}\left({\mathbf{B}}_{\text{ global }},M_{\text{ global }}\right)\right]\\ +{\mathbb{E}}_{{\mathbf{B}}_{1:T,{\mathbf{z}}_{1:T}}}[\log \left(1-D_{\text{ global }}\left({\mathbf{B}}_{\text{ global }}\left({\mathbf{B}}_{\text{ global }}\left({\mathbf{B}}_{1:T},{\mathbf{z}}_{1:T}\right)\right)\right)\right]\end{array}$$

此外作者发现附加一个重构损失项${\mathcal{L}}_{\mathrm{r}\mathrm{e}\mathrm{c}}$（这里选择的是perceptual loss）会提高mask预测的准确性、训练的稳定性，记为：$${\mathcal{L}}_{\mathrm{r}\mathrm{e}\mathrm{c}}=\sum _l\Vert {\Phi }_l\left(G_{\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{l}}\right)-{\Phi }_l\left(M_{\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{l}}\right)\Vert$$

这一部分整体的目标函数为${\mathcal{L}}_{\text{ shape }}={\lambda }_i{\mathcal{L}}_{\text{ inst }}+{\lambda }_g{\mathcal{L}}_{\text{ global }}+{\lambda }_r{\mathcal{L}}_{\mathrm{r}\mathrm{e}\mathrm{c}}$

---

Image generation

这一部分的模型架构如下所示，整个模型是一个encoder-decoder架构的卷积神经网络，它是对Pixel2Pixwl的改进

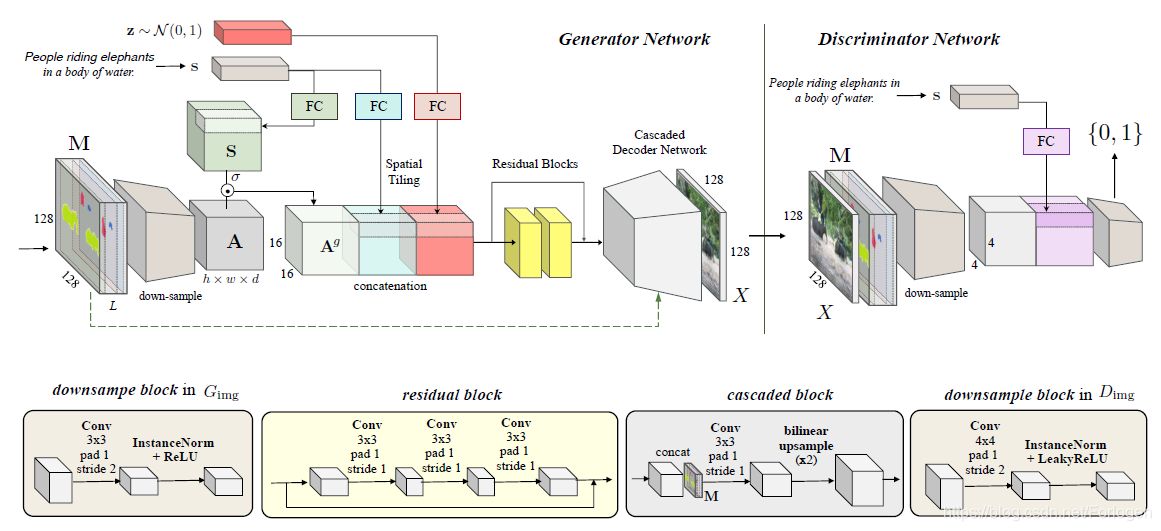
生成图像过程的表达式为$\hat{X}=G_{\mathrm{i}\mathrm{m}\mathrm{g}}(\mathrm{M},\mathrm{s},\mathrm{z})$，其中$M$为上一阶段生成的所有mask的聚合，$S$为输入文本的嵌入向量，$z$为随机噪声。具体流程为：

• M通过一系列的下采样层构建层特征$A\in R^{H\times W\times d}$。为了自适应地选择与文本相关的上下文，这里在布局特性上上使用了注意力机制
• 然后使用一个类似于LSTM中门的做法，从text得到一个d维向量，让后复制使它成为$H\times W\times d$的张量$S$，然后做${\mathbf{A}}^g=\mathbf{A}\odot \sigma (\mathbf{S})$
• 为了更好的编码文字中的背景信息，这里使用分开的全连接层和空间复制进行文本的嵌入。
• 然后，橘色部分就是对噪声向量进行空间复制，直接将三部分相连得到新的特征图，接下来将其输入到残差网络，然后d解码得到真实图像

$D_{img}$的目标函数记为${\mathcal{L}}_{\mathrm{i}\mathrm{m}\mathrm{g}}={\lambda }_a{\mathcal{L}}_{\mathrm{a}\mathrm{d}\mathrm{v}}+{\lambda }_r{\mathcal{L}}_{\mathrm{r}\mathrm{e}\mathrm{c}}$其中各部分分别为$$\begin{array}{rl}{\mathcal{L}}_{\mathrm{a}\mathrm{d}\mathrm{v}}=& {\mathbb{E}}_{(\mathbf{M},\mathbf{s},X)}\left[\log D_{\mathrm{i}\mathrm{m}\mathrm{g}}(\mathbf{M},\mathbf{s},X)\right]\\ & +{\mathbb{E}}_{(\mathbf{M},\mathbf{s}),\mathbf{z}}\left[\log \left(1-D_{\mathrm{i}\mathrm{m}\mathrm{g}}\left(\mathbf{M},\mathbf{s},G_{\mathrm{i}\mathrm{m}\mathrm{g}}(\mathbf{M},\mathbf{s},\mathbf{z})\right)\right)\right]\\ {\mathcal{L}}_{\mathrm{r}\mathrm{e}\mathrm{c}}=& \sum _l\Vert {\Phi }_l\left(G_{\mathrm{i}\mathrm{m}\mathrm{g}}(\mathbf{M},\mathbf{s},\mathbf{z})\right)-{\Phi }_l(X)\Vert \end{array}$$

在附录部分，作者给出了关于第一项更详细的描述：$$\begin{array}{rl}{\mathcal{L}}_{\mathrm{a}\mathrm{d}\mathrm{v}}=& {\mathbb{E}}_{(\mathbf{M},\mathbf{s},X)}\left[\log D_{\mathrm{i}\mathrm{m}\mathrm{g}}(\mathbf{M},\mathbf{s},X)\right]\\ & +{\mathbb{E}}_{(\mathbf{M},\tilde{\mathbf{s}},X)}\left[\log \left(1-D_{\mathrm{i}\mathrm{m}\mathrm{g}}(\mathbf{M},\tilde{\mathbf{s}},X)\right)\right]\\ & +{\mathbb{E}}_{(\mathbf{M},\mathbf{s}),\mathbf{z}}\left[\log \left(1-D_{\mathrm{i}\mathrm{m}\mathrm{g}}\left(\mathbf{M},\mathbf{s},G_{\mathrm{i}\mathrm{m}\mathrm{g}}(\mathbf{M},\mathbf{s},\mathbf{z})\right)\right)\right]\end{array}$$

它的想法来源于《Generative Adversarial Text to Image Synthesis》这篇文章中的损失项设计，如下所示： s r ← D ( x , h ) {  real image, right text  } s w ← D ( x , h ^ ) {  real image, wrong text  } s f ← D ( x ^ , h ) {  fake image, right text  } L D ← log ⁡ ( s r ) + ( log ⁡ ( 1 − s w ) + log ⁡ ( 1 − s f ) ) / 2 \begin{array}{l}{s_{r} \leftarrow D(x, h)\{\text { real image, right text }\}} \\ {s_{w} \leftarrow D(x, \hat{h})\{\text { real image, wrong text }\}} \\ {s_{f} \leftarrow D(\hat{x}, h)\{\text { fake image, right text }\}} \\ {\mathcal{L}_{D} \leftarrow \log \left(s_{r}\right)+\left(\log \left(1-s_{w}\right)+\log \left(1-s_{f}\right)\right) / 2}\end{array} sr​←D(x,h){ real image, right text }sw​←D(x,h^){ real image, wrong text }sf​←D(x^,h){ fake image, right text }LD​←log(sr​)+(log(1−sw​)+log(1−sf​))/2​

那么对应到本文中的损失项${\mathcal{L}}_{\mathrm{a}\mathrm{d}\mathrm{v}}$可以看出

• 第一部分表示mask+与之对应的正确句子+真实的图片
• 第二部分表示mask+随机生成的错误的句子+真实的图片
• 第三部分表示mask+与之对应的正确句子+假的图片

Experiment

文中给出了具体的实验结果，这里就不详细的写啦，只给出一张图有个直观的感受，感兴趣的还是好好研读原paper~

下图是本文提出的模型和其他模型的对比

下图显示的是每一步的效果

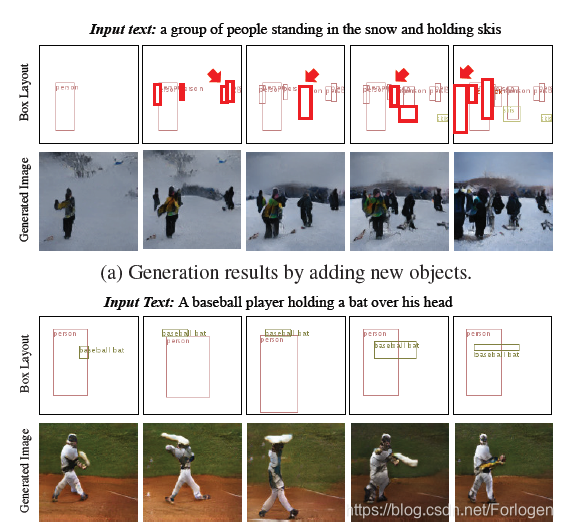
下图显示的是更改描述文本的不同部分就会生成相应的图像

下图显示的是改变布局，生成的图像中的实体也会做出相应的改变

总结

整体来看，本文的思想和以下的几篇文章具有一定的相似之处，都是希望借助一些中间步骤，不管是语义结构还是实体的布局等来帮助提高生成图像的质量，后面希望可以对这几篇文章做一个总结，找到它们额共通之处，并思考我们可以来做什么~

CVPR 2019 Object-driven Text-to-Image Synthesis via Adversarial Training
CVPR 2018 Inferring Semantic Layout for Hierarchical Text-to-Image Synthesis
CVPR 2019 Image Generation from Layout
CVPR 2019 Text2Scene: Generating Compositional Scenes from Textual Descriptions
ICLR 2019Generating Multiple Objects at Spatially Distinct Locations
NIPS 2016 Learning What and Where to Draw