NIPS 2016 《InfoGAN Interpretable Representation Learning by Information Maximizing Generative Adversarial Net》

背景
在2014年Goodfellow提出的最原始的GAN中,生成器
G
G
G接收一个随机的噪声
z
z
z 生成一个假样本,将生成的假样本
G
(
z
)
G(z)
G(z)和真实的样本
x
x
x一起丢给判别器
D
D
D ,然后判别器根据判别的结果给出一个标量,如果认为是真实样本就输出1,如果认为它是生成样本就输出0。那么
G
G
G希望生成的样本越接近真实越好,而
D
D
D希望可以最大程度的判断出样本的来源,这样就形成了一个对抗的过程。经过不断地训练,直到
G
G
G生成的样本不能被
D
D
D 判断出是来自哪里。这个minmax的对抗过程可以用如下的函数表示:
min
G
max
D
V
(
G
,
D
)
=
E
x
∼
p
d
a
t
a
(
x
)
l
o
g
D
(
x
i
)
+
E
x
∼
p
z
(
z
)
l
o
g
(
1
−
D
(
G
(
z
i
)
)
)
\min \limits_{G} \max \limits _{D} V(G,D)=E_{x \sim p_{data}(x) } logD(x_{i})+E_{x \sim p_{z}(z)}log(1-D(G(z_{i})))
GminDmaxV(G,D)=Ex∼pdata(x)logD(xi)+Ex∼pz(z)log(1−D(G(zi)))
但是在这个过程中,GAN并没有对
z
z
z 做任何的限制,即使最后
G
G
G可以生成一个不错的图像,我们也不知道
z
z
z和这个生成结果彼此之间有什么联系,即无法将
z
z
z的具体维度和生成图像的语义特征联系起来。而图像中的这些语义特征对于之后的一些其他的应用可能十分关键,所以如果我们希望能够从
z
z
z 和生成图像中,找到
z
z
z的维度和语义特征之间的对应关系,它也可以认为是一种表征学习的过程。
早期已经做了很多关于表征学习方面的工作,虽然可以取得一些不错的效果,但是它们往往都依赖于受监督的数据分组,但是很多情况下这些有标签的数据是很难获取到的。而GAN的出现很好的解决了这个难题,它可以自动的从数据中学习到一种分解表示。
而本文的InfoGAN就是借助GAN的这个优点,经过一些改造,使得InfoGAN可以从一系列的数据中自动的发现隐藏在其中的有意义的语义特征信息。
InfoGAN
在InfoGAN中,不再是将噪声 z z z直接输入到生成器中,而是将其分为了两个部分:
- z z z :表示不可压缩的原始噪声
- c c c :称为laten code,对应数据分布的潜在的语义向量
上面的 c c c可以用多个独立的变量 c 1 , c 2 , . . . , c L c_{1},c_{2},...,c_{L} c1,c2,...,cL 表示,假设它们满足 p ( c 1 , c 2 , . . . , c L ) = ∏ i = 1 L p ( c i ) p(c_{1},c_{2},...,c_{L})=\prod_{i=1}^{L}p(c_{i}) p(c1,c2,...,cL)=∏i=1Lp(ci) ,但是为了方面下面公式的推导,我们统一使用 c c c 来表示。
下面先给出InfoGAN的结构图(图片源自 https://github.com/hwalsuklee/tensorflow-generative-model-collections )
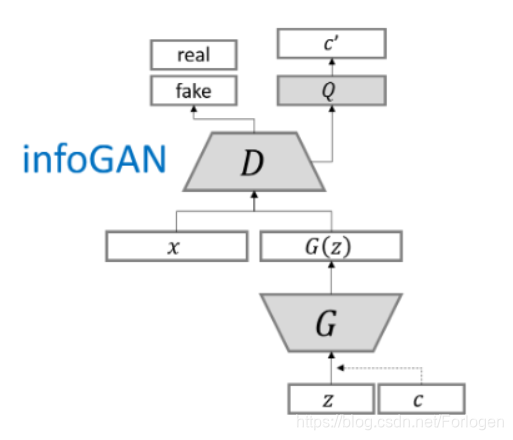
宏观上看InfoGAN可以分为三个部分:
- 生成网络 G G G
- 判别真伪的网络 D D D
- 判别类别的网络 Q Q Q
下面我们按照InfoGAN的数据流向来看一下它到底是如何实现上面提到的功能的。首先我们将传统的噪声分为了 z z z和 c c c两部分一起传到 G G G中,但是如果只是将噪声输入分解一下,其他部分不作任何改变的话,生成器生成的结果将最后忽略 c c c 的作用,即 P G ( x ∣ c ) = P ( x ) P_{G}(x|c) = P(x) PG(x∣c)=P(x),那么就违背了分解的初衷。那怎么解决这个问题呢?这里作者引入了互信息(mutual Information),下面在继续往前走之前,先简单的了解一下互信息是什么。
互信息
在概率论和信息论中,两个随机变量的互信息(Mutual Information,简称MI)或转移信息(transinformation)是变量间相互依赖性的量度。不同于相关系数,互信息并不局限于实值随机变量,它更加一般且决定着联合分布 $p(X,Y) $ 和分解的边缘分布的乘积 $p(X) 、 、 、p(Y) $ 的相似程度。它是度量两个事件集合之间的相关性(mutual dependence),最常用的单位是bit。
定义
对于两个离散的随机变量
X
X
X 和
Y
Y
Y ,它们的互信息定义如下:
I
(
X
,
Y
)
=
∑
y
∈
Y
∑
x
∈
X
p
(
x
,
y
)
log
(
p
(
x
,
y
)
p
(
x
)
p
(
y
)
)
I(X,Y) = \sum_{y\in Y}\sum_{x \in X} p(x,y)\log (\frac{p(x,y)}{p(x)p(y)})
I(X,Y)=y∈Y∑x∈X∑p(x,y)log(p(x)p(y)p(x,y))
其中
p
(
X
,
Y
)
p(X,Y)
p(X,Y) 是关于
X
X
X 和
Y
Y
Y 的联合概率分布函数,
p
(
x
)
p(x)
p(x)和
p
(
y
)
p(y)
p(y) 分别是关于
X
X
X和
Y
Y
Y的边缘概率分布函数。
对于两个连续的随机变量,它们的互信息定义如下:
I
(
X
,
Y
)
=
∫
Y
∫
X
p
(
x
,
y
)
log
(
p
(
x
,
y
)
p
(
x
)
p
(
y
)
)
d
x
d
y
I(X,Y) = \int _{Y} \int_{X}p(x,y)\log (\frac{p(x,y)}{p(x)p(y)})dxdy
I(X,Y)=∫Y∫Xp(x,y)log(p(x)p(y)p(x,y))dxdy
直观上可以将其理解为两个变量
X
X
X和
Y
Y
Y之间共享信息多少的度量,如果互信息越大,我们知道其中一个变量的信息,对于另一个变量知道的信息就越多;反之互信息越小,彼此之间提供的信息就会越少。
互信息和其他度量的关系


互信息可以表示为如下的形式:
I
(
X
;
Y
)
=
H
(
X
,
Y
)
−
H
(
X
∣
Y
)
−
H
(
Y
∣
X
)
I(X;Y)=H(X,Y)-H(X|Y)-H(Y|X)
I(X;Y)=H(X,Y)−H(X∣Y)−H(Y∣X)
其中
H
(
X
)
H(X)
H(X)和
H
(
Y
)
H(Y)
H(Y) 是边缘熵,
H
(
X
∣
Y
)
H(X|Y)
H(X∣Y) 和
H
(
Y
∣
X
)
H(Y|X)
H(Y∣X) 是条件熵,
H
(
X
,
Y
)
H(X,Y)
H(X,Y) 是
X
X
X和
Y
Y
Y的联合熵。它们的关系用韦恩图表示如上所示。
因此按照互信息的意思,如果输入到生成器中的噪声和生成的图像存在一定的潜在的对应关系,那么
c
c
c和
G
(
z
,
c
)
G(z,c)
G(z,c)之间应该就应该有很大的互信息量,即
I
(
c
;
G
(
z
,
c
)
)
I(c;G(z,c))
I(c;G(z,c)) 的值应该很大。那么InfoGAN对应的
V
(
G
,
D
)
V(G,D)
V(G,D) 就成了如下的形式:
min
G
max
D
V
1
(
G
,
D
)
=
V
(
G
,
D
)
−
λ
I
(
c
;
G
(
z
,
c
)
)
=
E
x
∼
p
d
a
t
a
(
x
)
l
o
g
D
(
x
i
)
+
E
x
∼
p
z
(
z
)
l
o
g
(
1
−
D
(
G
(
z
i
)
)
)
−
λ
I
(
c
;
G
(
z
,
c
)
)
\min \limits_{G} \max \limits _{D} V_{1}(G,D)=V(G,D)-\lambda I(c;G(z,c)) \\ =E_{x \sim p_{data}(x) } logD(x_{i})+E_{x \sim p_{z}(z)}log(1-D(G(z_{i})))-\lambda I(c;G(z,c))
GminDmaxV1(G,D)=V(G,D)−λI(c;G(z,c))=Ex∼pdata(x)logD(xi)+Ex∼pz(z)log(1−D(G(zi)))−λI(c;G(z,c))
其中
λ
\lambda
λ是引入的超参数,作者指出如果是离散的laten code,那么使
λ
=
1
\lambda=1
λ=1就足够了;如果是连续性的laten code,那么要使用小一点的
λ
\lambda
λ 。
但在求解上面的minmax问题时,我们很难直接最大化
I
(
c
;
G
(
z
,
c
)
)
I(c;G(z,c))
I(c;G(z,c))这一项,因为在计算它时需要后验概率项
P
(
c
∣
x
)
P(c|x)
P(c∣x)。为了解决这个问题,引入一个辅助分布
Q
(
c
∣
x
)
Q(c|x)
Q(c∣x) ,通过获取到的
Q
(
c
∣
x
)
Q(c|x)
Q(c∣x)的下确界来逼近
P
(
c
∣
x
)
P(c|x)
P(c∣x),从而得到关于它的近似解。具体的数学推导如下所示:
I
(
c
;
G
(
z
,
c
)
)
=
H
(
c
)
−
H
(
c
∣
G
(
z
,
c
)
)
=
E
x
∼
P
G
(
x
∣
z
,
c
)
E
c
∼
P
(
c
∣
x
)
log
P
(
c
′
∣
x
)
+
H
(
c
)
=
E
x
∼
P
G
(
x
∣
z
,
c
)
[
E
c
′
∼
P
(
c
′
∣
x
)
log
P
(
c
′
∣
x
)
Q
(
c
′
∣
x
)
+
E
c
′
∼
P
(
c
∣
x
)
log
Q
(
c
′
∣
x
)
]
+
H
(
c
)
=
E
x
∼
P
G
(
x
∣
z
,
c
)
[
K
L
(
P
(
c
′
∣
x
)
∥
Q
(
c
′
∣
x
)
)
⎵
⩾
0
+
E
c
′
∼
P
(
c
∣
x
)
log
Q
(
c
′
∣
x
)
]
+
H
(
c
)
⩾
E
x
∼
P
G
(
x
∣
z
,
c
)
E
c
′
∼
P
(
c
∣
x
)
log
Q
(
c
′
∣
x
)
+
H
(
c
)
\begin{aligned} I(c ; G(z, c)) &=H(c)-H(c | G(z, c)) \\ &=E_{x \sim P_{G}(x | z, c)} E_{c \sim P(c | x)} \log P(c' | x)+H(c) \\ &=E_{x \sim P_{G}(x | z, c)}\left[E_{c' \sim P(c' | x)} \log \frac{P(c' | x)}{Q(c' | x)}+E_{c' \sim P(c | x)} \log Q(c' | x)\right]+H(c) \\ &=E_{x \sim P_{G}(x | z, c)}\left[\underbrace{K L(P(c' | x) \| Q(c' | x))}_{\geqslant 0}+E_{c' \sim P(c | x)} \log Q(c' | x)\right]+H(c) \\ & \geqslant E_{x \sim P_{G}(x | z, c)} E_{c' \sim P(c | x)} \log Q(c' | x)+H(c) \end{aligned}
I(c;G(z,c))=H(c)−H(c∣G(z,c))=Ex∼PG(x∣z,c)Ec∼P(c∣x)logP(c′∣x)+H(c)=Ex∼PG(x∣z,c)[Ec′∼P(c′∣x)logQ(c′∣x)P(c′∣x)+Ec′∼P(c∣x)logQ(c′∣x)]+H(c)=Ex∼PG(x∣z,c)⎣⎡⩾0
KL(P(c′∣x)∥Q(c′∣x))+Ec′∼P(c∣x)logQ(c′∣x)⎦⎤+H(c)⩾Ex∼PG(x∣z,c)Ec′∼P(c∣x)logQ(c′∣x)+H(c)
其中
x
x
x是
G
(
c
,
z
)
G(c,z)
G(c,z)的观测值,
c
′
∼
P
(
c
∣
x
)
c'\sim P(c|x)
c′∼P(c∣x)表示
x
x
x一个后验概率的观测值,
然后再使用一个引理
F
o
r
r
a
n
d
o
m
v
a
r
i
a
b
l
e
s
X
,
Y
a
n
d
f
u
n
c
t
i
o
n
f
(
x
,
y
)
u
n
d
e
r
s
u
i
t
a
b
l
e
r
e
g
u
l
a
r
i
t
y
c
o
n
d
i
t
i
o
n
s
:
E
x
∼
X
,
y
∼
Y
∣
x
[
f
(
x
,
y
)
]
=
E
x
∼
X
,
y
∼
Y
∣
x
,
x
′
∼
X
∣
y
[
f
(
x
′
,
y
)
]
For\ random\ variables\ X, Y\ and\ function\ f(x, y)\ under\ suitable\ regularity\ conditions:\ \\ \mathbb{E}_{x \sim X, y \sim Y|x}[f(x, y)]=\mathbb{E}_{x \sim X, y \sim Y\left|x, x^{\prime} \sim X\right| y}\left[f\left(x^{\prime}, y\right)\right]
For random variables X,Y and function f(x,y) under suitable regularity conditions: Ex∼X,y∼Y∣x[f(x,y)]=Ex∼X,y∼Y∣x,x′∼X∣y[f(x′,y)]
来定义一个变分的下界
L
1
(
G
,
Q
)
L_{1}(G,Q)
L1(G,Q) :
L
I
(
G
,
Q
)
=
E
c
∼
P
(
c
)
,
x
∼
G
(
z
,
c
)
[
log
Q
(
c
∣
x
)
]
+
H
(
c
)
=
E
x
∼
G
(
z
,
c
)
[
E
c
′
∼
P
(
c
∣
x
)
[
log
Q
(
c
′
∣
x
)
]
]
+
H
(
c
)
≤
I
(
c
;
G
(
z
,
c
)
)
\begin{aligned} L_{I}(G, Q) &=E_{c \sim P(c), x \sim G(z, c)}[\log Q(c | x)]+H(c) \\ &=E_{x \sim G(z, c)}\left[\mathbb{E}_{c^{\prime} \sim P(c | x)}\left[\log Q\left(c^{\prime} | x\right)\right]\right]+H(c) \\ & \leq I(c ; G(z, c)) \end{aligned}
LI(G,Q)=Ec∼P(c),x∼G(z,c)[logQ(c∣x)]+H(c)=Ex∼G(z,c)[Ec′∼P(c∣x)[logQ(c′∣x)]]+H(c)≤I(c;G(z,c))
从结果可以看到
c
′
c'
c′ 消失了。最终我们得到:
min
G
,
Q
max
D
V
InfoGAN
(
D
,
G
,
Q
)
=
V
(
D
,
G
)
−
λ
L
I
(
G
,
Q
)
\min _{G, Q} \max _{D} V_{\text { InfoGAN }}(D, G, Q)=V(D, G)-\lambda L_{I}(G, Q)
G,QminDmaxV InfoGAN (D,G,Q)=V(D,G)−λLI(G,Q)
生成器
G
G
G和判断类别网络
Q
Q
Q目标是使后面的式子尽量小,一方面是
G
G
G要使生成的样本骗过D
,
从
而
使
,从而使
,从而使
V
(
G
,
D
)
V(G,D)
V(G,D)尽量小,另一方面是
G
,
Q
G,Q
G,Q要尽可能的增大
L
1
(
G
,
Q
)
L_{1}(G,Q)
L1(G,Q),这样就可以实现InfoGAN的最主要的功能,加上负号后,整个式子就小。
实验
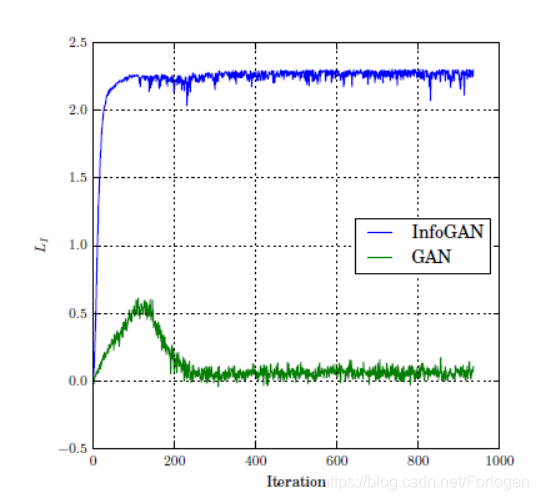
关于实验部分,我们主要看两张实验结果图。第一张图如下所示,它证明了InfoGAN中采取的方式可以很快的到达互信息最大的位置,而相比之下GAN表现的就很差,表明InfoGAN比GAN更好的可以建立 c c c 的维度和生成图像的语义特征之间的联系。
第二张图如下所示,它在MNIST数据集中显示了 c c c的不同维度和生成图像的语义特征的具体联系。比如 c 1 c_{1} c1是联系生成图像的数字类型; c 2 c_{2} c2联系数字的旋转特征; c 3 c_{3} c3联系数字的笔画粗细。

总之,作者经过实验证明了InfoGAN可以在完全无监督的方式下,在关于学习数据集上的可解释性的语义特征方面,可以取得很好的效果。
参考
https://blog.youkuaiyun.com/Feynman1999/article/details/86545075
https://blog.youkuaiyun.com/a312863063/article/details/83575933
https://blog.youkuaiyun.com/a358463121/article/details/82869603























 1133
1133

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








