林轩田机器学习技法课程第十三讲-Deep Learning

最新推荐文章于 2019-12-31 15:46:43 发布

Forlogen

最新推荐文章于 2019-12-31 15:46:43 发布

阅读量405

点赞数

CC 4.0 BY-SA版权

分类专栏：林轩田机器学习技法课程

本文链接：https://blog.youkuaiyun.com/Forlogen/article/details/89293766

林轩田机器学习技法课程专栏收录该内容

11 篇文章

订阅专栏

本文探讨了深度学习网络架构的选择，包括浅层网络和深层网络的特点与应用场景，以及网络权重初始化的重要性。介绍了Autoencoder和Linear Autoencoder的概念，及其与主成分分析（PCA）的关系，讨论了模型复杂度控制和过拟合的正则化方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

这一讲的是对Deep Learning这个热门方向的一个介绍，虽然很多知识在现在看起来有点老了，但还是有很多的启发意义。主要从以下四个面进行介绍：

Deep Neutral Network
Autoencoder
Denoising Autoencoder
Principal Component Analysis

下图是在第12讲中提到了一个关于神经网络的简单的示例，它包括输入层、两个隐藏层和一个输出层，在层与层之间是转换的权重矩阵，每个隐藏层中的神经元的激活函数为 $t a n h$ ，输出层为线性输出。同样为了方便计算，这里在每一层中添加了 $x_{0}^{i}=1$ 。其中每一个的隐藏层负责从输入的数据中来发现某些有趣的东西，或说是有关数据的某种模式。
在这里插入图片描述

那么在设计神经网络的时候，我们应该选择多少层？每一层中包含多少了神经元呢？或者说什么样的网络架构才是最好的呢？严格来说，我们很难设计出一个通用性和效果都很好的网络，在实际中往往是针对具体的问题设计相关的架构，所以出现了类如VGG、Res-Net等等架构方式。也许你会想我们能否在不同的架构中使用之前学习的验证方式来找到最好的呢？答案是这样的方式是不太实际的！针对于网络架构的研究也有很多人在做，比如最近何凯明发的一篇论文阐述了随机连接的网络性能要优于人工精心设计的网络，有兴趣的可以看一下。

那么如何来选择不同的网络架构呢？通常来说，我们可以讲其分为如下的两大类：

Shallow net：它表示网络中含有较少的隐藏层，使用这样的构架方式，它的有点在于：网络的训练更加有效、网络结构简单、理论上如果有足够的神经元，它的能力也会足够的强
Deep Net：它表示网络中含有很多的隐藏层，使用这样的方式，由于网络很深，参数众多，训练难度自然也就很大；结构更加的复杂；理论上，如果我们网络足够的深、神经元足够的多，模型的能力自然也会足够的强；此外它相比浅层的网络，得到的结果更加的有意义。所以如果我们的网络设计的足够的深、足够的好，理论上它可以解决很多之前无法解决的问题，因此deep learning 在如今如此的火爆。

那么通过deep net得到的结果更加有意义是什么意思呢？我们知道在deep net中会有很多的隐藏层，那么不同的层就会提取出数据中不同的特征，层数越多，提取出的特征的个数就越多。而且每一层提取的特征都具有相应的物理意义。这种各司其职的方式建立的网络，在解决复杂问题方面的能力就越强，效果就会更好。。

但是deep learning同样有一些问题需要引起我们的注意，如下所示：

模型结构的选择：因为网络中的层数、神经元的个数都不是固定，我们我们需要针对不同的问题，选择合适的网络架构。比如在处理图像问题中，我们会使用CNN；在处理序列数据时，我们会使用RNN……这样的选择需要网络的架构这具有一定的领域知识
模型的复杂度：随着层数和神经元数量的增加，模型的复杂度自然也会增加。当模型的复杂度很高时，处理起来就会有很大的挑战。但在现在看来，如果我们的数据足够的多，它似乎也不是一个很大的问题；另外我们还可以使用很多的手段来降低模型的复杂度，比如dropout、denosing……
模型的优化：当网络很复杂时，所涉及的权重参数就会非常的多，这给网络的优化带来了很大的挑战。缓解这个问题的一种方法就是注重权重的初始化，避免在参数更新时困在局部的最小值，这种方式也成为预训练。当然在初始化权重方面，现在也有很多的方法可供选择，网络上也有很好别人预训练好的模型供我们使用。
模型的计算复杂度网络越复杂参数越多，计算量就会越大，同时当数据量变大时，同样也会增加模型的计算复杂度。但是在实际中，随着硬件的进步和并行处理技术的发展，使我们可以考虑选择使用很复杂的网络，而不用太过于在意训练的时长。

在上面提到，网络权重的初始化选择很重要，好的初始值能够帮助避免受困于局部最优解。常用的方法就是先进行预训练，得到权重的初始化值，然后在正式的训练中，使用后向传播来微调参数，使最后得到的模型效果更好。基本流程如下所示：
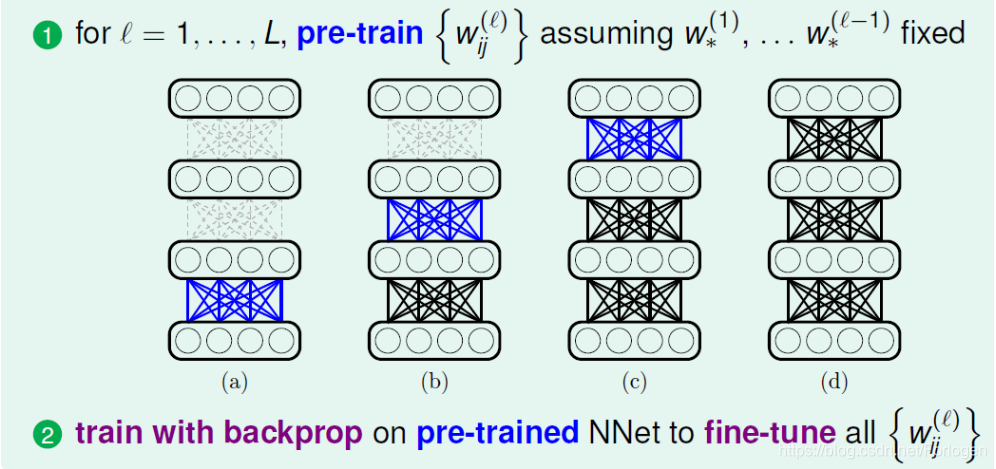
在这里插入图片描述

那么网络中的权重是什么呢？在神经网络中，权重可以认为是一种转换，将某一层的特征转换成后一层表示的方式；或者说完成一种编码（encoding）的过程，将某一层的特征使用另一种编码表示。所以好的权重初始值应该是尽可能地保留数据的特征信息，如果我们使用它来重建输入的数据，得到的结果应该很输入很相似。

下面我们使用下图来看一下尽可能的保留特征的信息是什么意思？
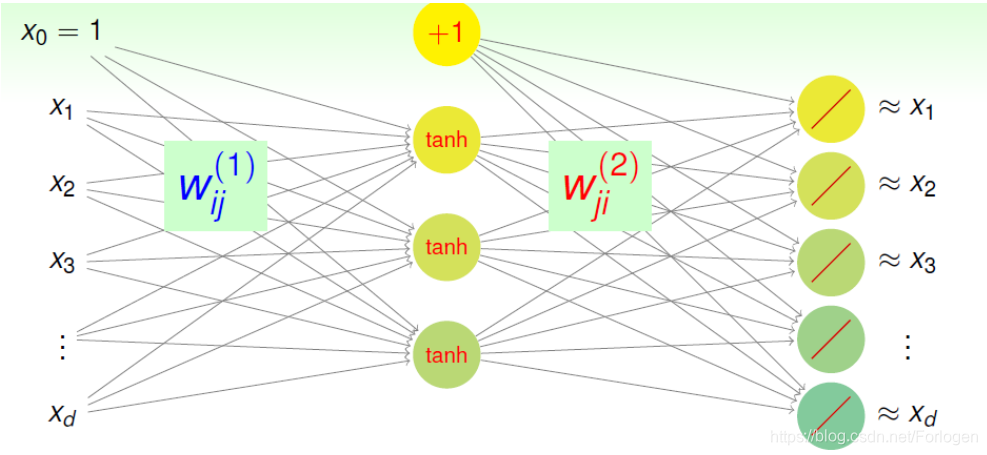
在这里插入图片描述

如上图所示，网络只有输入层、一个隐藏层和输出层三层，层与层之间有权重矩阵 $W_{ij}^1$ 和 $W_{ij}^2$ 。整个网络可以看成是 $-\ \check{d} -\ d$ 的结构，其中输入层到隐藏层可以看作encoding的过程，隐藏层到输出层可以看作decoding的过程，那么整个网络就可以看作是一个Autoencoder。我们希望输入经过这个Autoencoder后，输出的结果和对应的输入尽可能的相似，这个过程类似于学习得到 $g $ ，使 $g (x) \approx x $ 。

那么使用Autoencoder这样形式的网络有什么好处呢？总体来说，通过这样的结构，我们可以更好的观察到数据中隐藏的结构信息。

监督学习： 隐藏层的输出可以看成使对原始数据完成了一次特征转换，从中可以得到一些更有代表性的信息
无监督学习： 可以用来做密度估计，或者说是判断原始数据的稀疏程度。如果 $g (x) \approx x$ ，则表示密度较大；如果g(x)与x差别很大，则表示密度较小。使用这样的思想，我们也可以用来进行离群点的探测，找出哪些数据是典型的，哪些是关系不大的，这样就可以从原始数据中学习到一些典型的表达信息

对于Basic Autoencoder来说，它的结构是如上面所述的 $-\ \check{d} -\ d$ ，因为希望重建后的结果和原始的输入尽可能的相似，所以误差评估函数为平方误差 $∑i=1d(gi(x)−xi)2\sum_{i=1}^d (g_{i}(x)-x_{i})^2$ 。此外它还具有如下的特点：

基本的Autoencoder只包括基本的三层，因此使用后向传播的计算量较小，便于训练
隐层的大小为 $dˇ\check{d}$ 满足 $dˇ<d\check{d} < d$ ，因此它往往可以得到原始数据的一种压缩表示，便于编码
因为我们的输出是对于输入的逼近，因此可以看成是一种无监督的学习
通常会添加限制条件 $W_{ij}^{(1)}=W_{ij}^{(2)}$ ，将其作为一种正则化的手段，但是在计算梯度时会变的复杂一些

通常使用Autoencoder做一个预训练的事情，从对无标签的数据经过编码、解码的过程中，学习到一个有意义的编码权重 $W_{ij}$ ，将其做为后面神经网络一个比较好的初始化权重。

因此在每两层之间，我们都可以使用Autoencoder进权重的初始化，然后在正式的训练中，再根据数据使用后向传播进行参数的微调，最后获得一个效果还不错的模型。
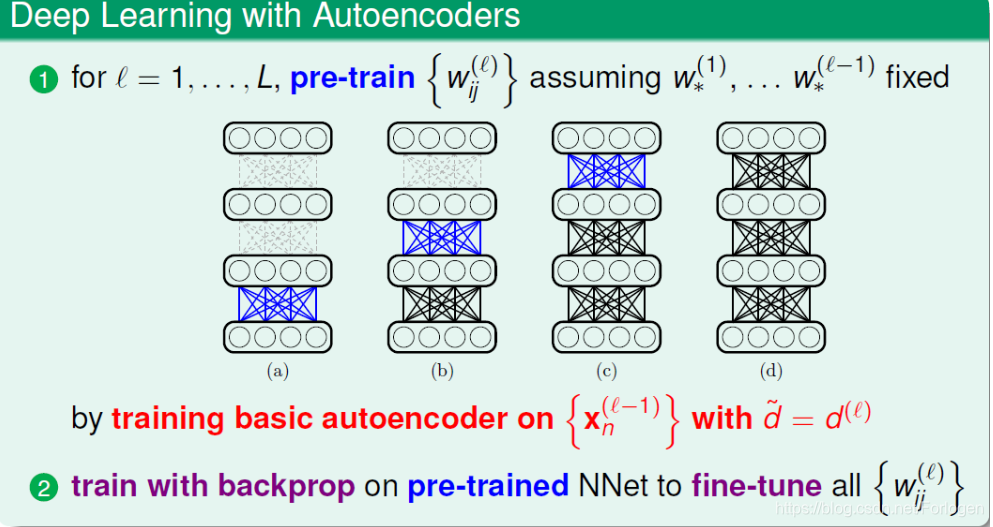
在这里插入图片描述

我们可以使用Autoencoder来进行权重的初始化工作，，完成一个预训练的工作。下面来看一下如何使用一些正则化（regularization）的方式来控制模型的复杂度。因为当我们的网络很复杂的时候，它可以学得很好，能力很强，但是同时也可能出现过拟合，导致泛化能力下降。像在机器学习中一样，我们也可以使用正则化的方式来控制模型的复杂度。

常见的方法有：

对于网络结构做一些限制
权重衰减、权重消除
早停

在介绍另一种方法之前，先看一下导致过拟合出现的原因有哪些。下面这张图是不是很熟悉呢?它就是之前基石课程中很重要的观察数据量、噪声大小和过拟合之间的关系的一张图。从图中我们可以看出，当样本数量下降、噪声变大都会造成overfitting的出现。
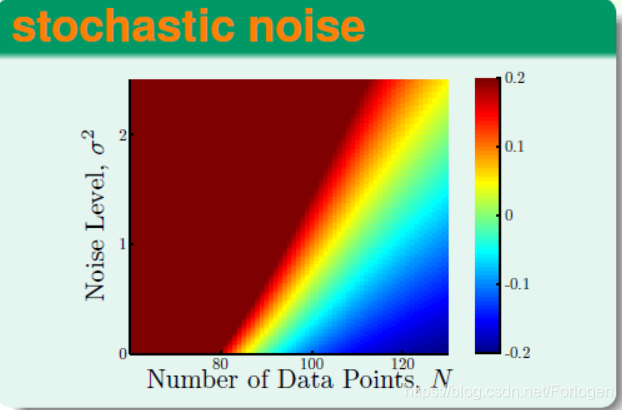
在这里插入图片描述

就噪声而言，我们有什么办法降低它的影响呢？最直观的方法可能就是对源头进行治理，即对数据进行清理，使它包含的噪声足够的小，这样训练得到的模型效果看起来就不会很差。但是这样的结果模型只能保证 $g (x) \approx x$ ，当数据稍微不同时，或有一点噪声时，效果就会很差。所以另一种相对的方法是我们不去尝试减少数据中的噪声，反正人工条件一些噪声，则输入变成 $noise\check{x} =x_{i}+artificial\ noise$ ,希望 $g(xˇ)≈xg(\check{x}) ≈ x$ 。经过训练得到的模型，不仅在训练数据上表现得很好，在新的含有噪声的数据上，同样可以有不错的效果，这样我们就得到了一下鲁棒性更好的网络模型。

前面给出的网络示例中，因为激活函数为tanh，所以它其实是一个非线性的自动编码器（nonlinear autoencoder）。下面来看一下linear autoencoder，并且看一下它和主成分分析（PCA）有什么联系。

在linear autoencoder中不适用非线性的激活函数，因此第K层的部分可以表示成如下的形式
$h_{k}(x)=\sum_{j=0}^{\check{d}}w_{jk}^{(2)}(\sum_{i=0}^{d} w_{ij}^{(1)}x_{i})$
同时有三个特殊的限制条件：

移除加入的 $x_{0}$ ，因为我们希望输出尽可能地接近输入，那么让1逼近1就没有什么意义
限制 $W_{ij}^{(1)}=W_{ij}^{(2)}=W_{ij}$
使得 $dˇ<d\check{d} < d$

那么上面的 $h (x)$ 就可以写成 $h(x)=WW^{T}x$ 。

从Error function的角度来看，我们希望 $E_{in}$ 尽可能的小，即希望下式尽可能地小，求出对应的 $W$ 。
$E_{in}(h)=E_{in}(W)=\frac{1}{N}\sum_{n=1}^{N}||x_{n}-WW^{T}x_{n}||^2$
其中 $WW^{T}$ 是半正定矩阵，半正定矩阵有性质 $VV^{T}=V^{T}V=I_{d}$ 。那么根据性质，对 $WW^{T}$ 进行特征值分解有 $WWT=VΓVTWW^{T}=V\Gamma V^{T}$ ，其中 $Γ\Gamma$ 为对角阵，非零元素不超过 $dˇ\check{d}$ 。同样的我们将 $x_{n}$ 进行类似的操作，得到 $x_{n}=VIV^{T}x_{n}$ ，其中 $Id×dI_{d\times d}$ 为单位阵。

这样就将对 $W$ 的优化问题转变为对 $V$ 和 $Γ\Gamma$ 的优化问题了。即如下所示：
$\min \limits_{V} \max \limits_{\Gamma} \frac{1}{N} \sum_{n=1}^{N}||VIV^{T}x_{n}-V \Gamma V^{T}x_{n}||^2$
首先来看内层关于 $Γ\Gamma$ 的优化问题：
$min⁡Vmax⁡Γ1N∑n=1N∣∣VIVTxn−VΓVTxn∣∣2\min \limits_{V} \color{lime}{\max \limits_{\Gamma} \frac{1}{N} \sum_{n=1}^{N}||VIV^{T}x_{n}-V \Gamma V^{T}x_{n}||^2}$
我们希望最小化上式，相当于希望 $(I−Γ)(I-\Gamma)$ 越小越好，即对角线上的零越多越好。因为 $Γ\Gamma$ 的秩最大为 $dˇ\check{d}$ ,所以最多有 $dˇ\check{d}$ 个1，相对应的可以认为是 $(I−Γ)(I-\Gamma)$ 最多有 $d−dˇd-\check{d}$ 个1， $Γ\Gamma$ 的最优解表示如下：
$\min \limits_{V}\sum_{n=1}^{N}||\begin{bmatrix} 0 & 0 \\ 0 & {I_{d-\check{d}}} \\ \end{bmatrix}V^{T}x_{n}||^2$
然后将其转换成对偶的最大化问题，如下所示：
$\min \limits_{V}\sum_{n=1}^{N}||\begin{bmatrix} 0 & 0 \\ 0 & {I_{d-\check{d}}} \\ \end{bmatrix}V^{T}x_{n}||^2= \max \limits_{V}\sum_{n=1}^{N}||\begin{bmatrix} {I_{\check{d}}} & 0 \\ 0 & 0 \\ \end{bmatrix}V^{T}x_{n}||^2$
其中当 $dˇ=1\check{d}=1$ 时， $V^{T}$ 中只有第一行 $v^{T}$ 有用，因此可以将上述的最大化问题转化为：
$\max \limits_{v} \sum_{n=1}^{N}v^{T}x_{n}x_{n}^{T}v\ ,\ subject\ to\ v^{T}v=1$
对于这样有条件的问题我们可以使用拉格朗日乘子法，引入拉格朗日因子 $λ\lambda$ ，即
$\sum_{n=1}^{N}x_{n}x_{n}^{T}v=\lambda v$
根据线性代数可以知道， $v$ 就是 $X^{T}X$ 的特征向量，而 $λ\lambda$ 就是相对应的特征值。我们要求的是最大值，所以最优解 $v$ 就是 $X^{T}X$ 最大特征值对应的特征向量。当 $dˇ>1\check{d} > 1$ 时，解法类似，最优解 $v_{j}$ 就是 $X^{T}X$ 前 $dˇ\check{d}$ 大的特征值对应的 $dˇ\check{d}$ 个特征向量。