CycleGAN

最新推荐文章于 2025-10-30 04:17:48 发布

原创最新推荐文章于 2025-10-30 04:17:48 发布 · 1.8k 阅读

10 ·

CC 4.0 BY-SA版权

Deep Learning 同时被 2 个专栏收录

50 篇文章

订阅专栏

GAN

46 篇文章

订阅专栏

ICCV 2017 《Unpaired Image-to-Image Translatin usig Cycle-Consistent Adversarial Networks》

github

这篇文章讲的就是大名鼎鼎的CycleGAN，它可以实现再无配对数据的情况实现不同域（domain）之间图像的互相转换。它的基本思想和前面讲过的DiscoGAN和DualGAN是一致的，同样只看一下它精髓的地方。

首先直观上看一下它的效果怎么样

在这篇文章之前，已经有很多方法来处理无配对样本的图像转换问题，比如Bayesian framework、CoGAN等，相比于这些方法，CycleGAN有如下的优点：

它的通用性更强，不依赖于具体的任务
它不需要预先定义输入和输出之间的相似性函数
它不依赖于输入和输出位于相同的低维嵌入空间的假设

下面我们再看一下它的架构

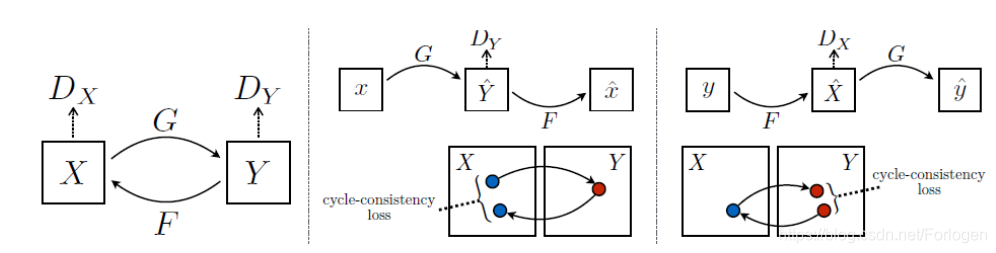
它使用两个生成器、两个判别器，通过构成环状的结构来实现两个域的图像之间相互转换，和DualGAN、DiscoGAN没什么本质的区别。

在CycleGAN中主要是包含两个损失项对抗损失（Adversarial loss）和循环一致性损失（Cycle Consistency loss）。

Adversarial loss

这部分和标准GAN的损失项是一致的，它们的数学表达如下所示：
$L_{GAN}(G,D_{Y},X,Y)=E_{y\sim p_{data}(y)}[\log D_{Y}(y)]+E_{x\sim p_{data}(x)}[\log (1-D_{Y}G(x))] \\ L_{GAN}(F,D_{X},Y,X)=E_{x\sim p_{data}(x)}[\log D_{X}(x)]+E_{y\sim p_{data}(y)}[\log (1-D_{x}F(y))]$
那么自然所有的G都希望生成的样本尽可能的接近于真实，而所有的D 都希望尽最大努力判别出真实样本和生成样本，所以我们的目标自然就是如下的形式：
$\min\limits_{G}\max \limits_{D_{Y}}L_{GAN}(G,D_{Y},X,Y) \\\min\limits_{F}\max \limits_{D_{X}}L_{GAN}(G,D_{X},Y,X)$

Cycle Consistency loss

这里同时使用的是 $L_{1}$ 度量，我们希望重构后的样本接近于输入，所以定义Cycle Consistency loss为如下的形式：
$L_{cyc}(G,F)=E_{x\sim p_{data}(x)}[||F(G(x))-x||_{1}]+E_{y\sim p_{data}(y)}[||G(F(y))-y||_{1}]$
将上面的两个损失项整合起来得到我们最终的目标函数是
$L(G,F,D_{X},D_{Y}) = L_{GAN}(G,D_{Y},X,Y)+L_{GAN}(F,D_{X},Y,X)+\lambda L_{cyc}(G,F)$
其中 $\lambda$ 是一个常数，控制两项损失的的相对重要性，在后面的实验中作者令 $\lambda = 10$ 。

那么通过对目标函数的最大最小化就可以得到最优的G和F：
$G^{*},F^{*} = arg\min \limits_{G,F} \max \limits_{D_{X},D_{Y}}L(G,F,D_{X},D_{Y})$

训练技巧

使用最小二乘损失（least-square loss）代替负的对数似然，这样做可以加强训练过程的稳定性，同时生成的结果更好。对于G来说，我们最小化的是
$E_{x\sim p_{data}(x)}[(D(G(x))-1)^2]$
对于D来说，我们需要最小化的是
$E_{y\sim p_{data}(y)}[(D(y)-1)^2]+E_{x\sim p_{data}(x)}[D(G(x))^2]$
使用生成图像的历史数据来更新判别器而不是最新生成的图像，所以开辟了一个存放50张历史图像的缓冲区
使用学习率初始化为0.0002，在训练的前100轮保持不变，在后100轮逐渐线性减小到0

实验

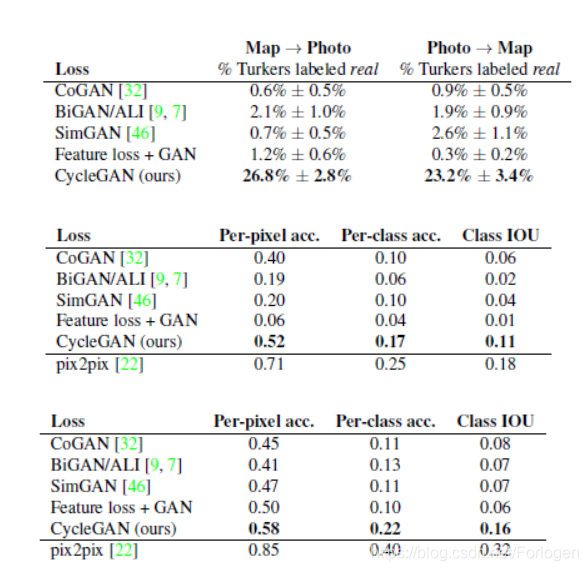
在实验的评估手段上同样使用的是AMT和FCN score，在Map->Photo和Photo->Map两个数据集上比较不同的GAN的变种之间的效果差异，结果如下所示

定性评估的结果，从中可以看出CycleGAN和pix2pix效果要优于其他的模型。

定量评估来看，无论是AMT的结果、FCN-scores还是分类的表现，CycleGAN都优于除pix2pix以外的模型，并且和pix2pix效果最为接近。

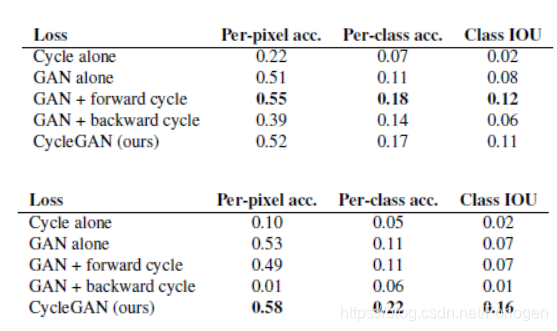
同样在评估两个损失向的重要性时发现，移除任何一个都会造成效果的大幅下降。另外如果只使用GAN+forward cycle或是GAN + backward cycle都会出现模式崩溃的问题，而且会影响训练过程的不稳定性。

在重构数据的质量方面，CycleGAN也取得不错的效果，重构后的图像很接近于输入的样本图像

此外作者还在有关图像的其他方面做了实验，证实了CycleGAN的效果要由于其它的模型。其中在从绘画中生成照片这项实验中，作者发现，当引进一个额外的损失项 $L_{identity}$ 后，输出图像的颜色部分更接近于输入图像。 $L_{identity}$ 的定义如下所示：
$L_{identity} (G,F)= E_{y\sim p_{data}(y)}[||G(y)-y||_{1}]+E_{x\sim p_{data}(x)}[||F(x)-x||_{1}]$
效果如下所示