朴素贝叶斯（Naive Bayesian）

引入

---

朴素贝叶斯是一种经典的机器学习的分类算法，基本原理很简单，学过概率论和数理统计的应该很容易理解。分类问题是人们日常生活中一种最常见的问题，比如我们需要分辨不同的人、在买菜或买水果时要分辨不同的类别等等，很多时候我们是基于之前的经验进行分类，贝叶斯分类算法也是这样的原理。它根据已有的分好类的数据学习一个分类器，当我们有一个新的实例的时候，将其输入到分类器，输出具有最大后验概率的类别就是我们最后需要的结果。

贝叶斯定理

---

贝叶斯定理是我们计算概率中很重要也是很常用的一个公式，它的形式如下：$$p(Y_k|X)=\frac{P(X{Y}_k)}{P(X)}=\frac{P(Y_k)p(X|Y_k)}{{\sum }_{j}P(Y_j)P(X|Y_j)}$$

• $P(X)$：计算X的概率值
• $P(Y|X)$ :计算在输入为X的情况下结果为Y的条件概率值
• $P(XY)$：计算X和Y的联合概率分布

为什么要用到贝叶斯定理呢？是因为在实际中，当我们已有一系列的分类已知的数据时，我们很容易计算出当是某一类别Y时输入为Xi时的条件概率$P(X_i|Y)$，但是在得到一个新的 $X$时，我们不容易计算出$P(Y|X)$，这时就要借助贝叶斯公式来换个方向继续求解。

朴素贝叶斯（naïve bayes）

---

贝叶斯分类算法有很多，我们首先来看朴素贝叶斯算法，它是一种生成模型，基于上面的贝叶斯定理和特征条件独立假设，广泛的用于一些分类问题。在朴素贝叶斯算法中，假设所有的数据都是独立同分布产生的，所以我们可以计算先验概率分布:$$P(Y=c_k),k=1,2,...,K$$

和条件概率分布$$P(X=x|Y=c_k)=P(X^{(1)}=x^{(1)},...,X^{(n)}=x^{(n)}|Y=c_k)$$

来求出数据集的联合概率分布$P(X,Y)$。

而条件独立性假设是说在分类确定的情况下，输入是哪一个$X$时，彼此之间是互不影响的（它在朴素贝叶斯中是很重要的一个假设，大大的简化了算法的学习和预测）。数学表达如下所示：$$P(X=x|Y=c_k)=P(X^{(1)}=x^{(1)},...,X^{(n)}=x^{(n)}|Y=c_k)=\prod _{j=1}^{n}P(X^{(j)}=x^{(j)}|Y=c_k)$$

首先我们看下朴素贝叶斯算法的具体描述（李航《统计学习方法》第三章），再看其中的细节问题。

我们要做的就是在训练数据集上计算先验概率和条件概率，得到贝叶斯的分类器$$y=f(x)=arg\underset{c_k}{\max }P(Y=c_k|X=x)=arg\underset{c_k}{\max }\frac{P(Y=c_k){\prod }_{j}P(X^{(j)}=x^{(j)}|Y=c_k)}{{\sum }_{k}P(Y=c_k){\prod }_{j}P(X^{(j)}=x^{(j)}|Y=c_k)}$$

因为分母对于所有的分类结果都是相同的，实际中我们需要考虑的形式如下$$y=f(x)=arg\underset{c_k}{\max }P(Y=c_k)\prod _{j}P(X^{(j)}=x^{(j)}|Y=c_k)$$

当我们得到一个新的实例 $x$ 时，将其带入上面的公式，我们就可以得到它属于不同类别的后验概率的分布情况，后验概率最大的类别就是我们的分类判别的最后结果，是不是很简单呢？

例子

---

在买西瓜时，我们是怎么样来判别西瓜的生熟呢，也许你听别人说过很多的经验，比如：看颜色、听敲击的声响、看瓜蔓等等，我们就以这个例子来看下它是怎么计算的。假设我们有如下的一个数据集，它的有10个数据，特征包含瓜蒂、形状和颜色，类别当然就是生熟喽！

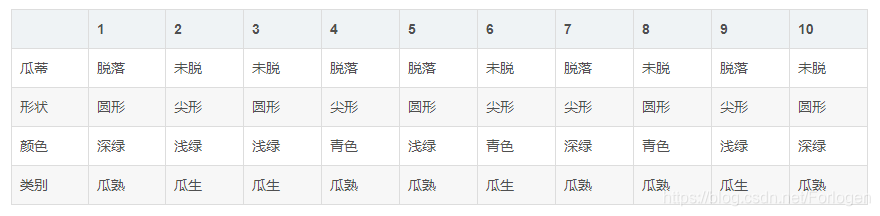
根据贝叶斯算法的描述我们首先需要计算先验概率和和条件概率：
$$P(瓜熟)=6/10，P(瓜生)=4/10P(瓜蒂=脱落|瓜熟)=4/6，P(瓜蒂=未脱落|瓜熟)=2/6$$$$P(形状=圆形|瓜熟)=4/6，P(形状=尖形|瓜熟)=2/4$$$$P(颜色=深绿|瓜熟)=3/6，P(颜色=浅绿|瓜熟)=1/6，P(颜色=青色|瓜熟)=2/6$$$$P(瓜蒂=脱落|瓜生)=1/4，P(瓜蒂=未脱落|瓜生)=3/4$$$$P(形状=圆形|瓜生)=1/4，P(形状=尖形|瓜生)=2/4$$$$P(颜色=深绿|瓜生)=0，P(颜色=浅绿|瓜生）=3/4，P(颜色=青色|瓜生)=1/4$$

当我们看到一颗瓜，它表现为瓜蒂脱落、形状圆形、颜色青色，那么它是生的还是熟的呢？我们就需要根据贝叶斯分类器计算相应的后验概率概率： $$\begin{gathered} P(瓜熟)\ast P(瓜蒂=脱落|瓜熟)\ast P(形状=圆形|瓜熟)\ast P(颜色=青色|瓜熟)=6/10\ast 4/6\ast 4/6\ast 2/6=0.0889 \\ P(瓜生)\ast P(瓜蒂=脱落|瓜生)\ast P(形状=圆形|瓜生)\ast P(颜色=青色|瓜生)=4/10\ast 1/4\ast 1/4\ast 1/4=0.0063 \end{gathered}$$
我们可以看出0.0889 > 0.0063，所以我们判断它是一颗熟瓜，就可以高高兴兴的回家吃瓜了。

在上面的计算中可以发现$P(颜色=深绿|瓜生)=0$，可能会影响后面的后验概率的计算，为了解决这个问题，我们常用的是使用贝叶斯估计，即在计算的时候加一个平滑量，常取值为1，称为拉普拉斯平滑，这时先验概率计算就变成了$$p_{\lambda }(Y=c_k)=\frac{{\sum }_{i=1}^{N}I(y_i=c_k)+\lambda }{N+K\lambda }$$

在引入了拉普拉斯平滑后，当样本数较少的时候避免了出现概率值为零的情况，而且当样本数变得足够多时，它所起到的影响作用就会越来越小，使得估计值更加接近真实值。总体来看，在引入拉普拉斯的朴素贝叶斯中存在着两个先验假设：

• 属性间的彼此独立的
• 属性值和类别均匀分布

实现代码

---

用于多分类的贝叶斯算法的实现：

# -*- coding: utf-8 -*-
"""
Created on Wed Nov 14 10:46:44 2018

@author: dyliang
"""
#https://blog.youkuaiyun.com/u012162613/article/details/48323777

import numpy as np

#多分类的朴素贝叶斯算法
class MultinomialNB(object):
    #alpha:平滑系数
    #fit_prior:是否学习到了先验概率
    #class_prior：类的先验概率
    def __init__(self,alpha=1.0,fit_prior=True,class_prior=None):
        self.alpha = alpha
        self.fit_prior = fit_prior
        self.class_prior = class_prior
        self.classes = None
        self.conditional_prob = None #条件概率

    #计算先验概率
    def _calculate_feature_prob(self,feature):
        #得到数据集的类别
        # np.unique():去除数组中的重复数字,并进行排序之后输出
        values = np.unique(feature)
        #类别总数 
        total_num = float(len(feature))
        value_prob = {}
        for v in values:
            #先验概率的贝叶斯估计
            value_prob[v] = (( np.sum(np.equal(feature,v)) + self.alpha ) /( total_num + len(values)*self.alpha))
        #返回每一类别的概率
        return value_prob

    #训练
    def fit(self,X,y):
        #训练集中分类的结果
        self.classes = np.unique(y)
        #计算类的先验概率: P(y=ck)
        #如果分类器不存在，重新训练
        if self.class_prior == None:
            class_num = len(self.classes)
            if not self.fit_prior:
                self.class_prior = [1.0/class_num for _ in range(class_num)]  
            else:
                self.class_prior = []
                sample_num = float(len(y))
                for c in self.classes:
                    c_num = np.sum(np.equal(y,c))
                    self.class_prior.append((c_num+self.alpha)/(sample_num+class_num*self.alpha))

        #计算条件概率: P(xj|y=ck)
        self.conditional_prob = {}  # 例如 { c0:{ x0:{ value0:0.2, value1:0.8 }, x1:{} }, c1:{...} }
        for c in self.classes:
            self.conditional_prob[c] = {}
            for i in range(len(X[0])):  #遍历特征
                feature = X[np.equal(y,c)][:,i]
                self.conditional_prob[c][i] = self._calculate_feature_prob(feature)
        return self


    #给定一些列的特征值 {value0:0.2,value1:0.1,value3:0.3,.. } 和目标值
    def _get_xj_prob(self,values_prob,target_value):
        return values_prob[target_value]

    #基于先验概率和条件概率预测单样本
    def _predict_single_sample(self,x):
        #初始化将其归到 -1
        label = -1
        #初始化最大后验概率为0
        max_posterior_prob = 0

        #对于每一类别，计算它的后验概率: class_prior * conditional_prob
        for c_index in range(len(self.classes)):
            current_class_prior = self.class_prior[c_index]
            current_conditional_prob = 1.0
            feature_prob = self.conditional_prob[self.classes[c_index]]
            j = 0
            for feature_i in feature_prob.keys():
                current_conditional_prob *= self._get_xj_prob(feature_prob[feature_i],x[j])
                j += 1

            #比较哪个后验概率最大
            if current_class_prior * current_conditional_prob > max_posterior_prob:
                max_posterior_prob = current_class_prior * current_conditional_prob
                label = self.classes[c_index]
        #返回分类的结果
        return label

    #预测          
    def predict(self,X):
        #如果是单样本
        if X.ndim == 1:
                return self._predict_single_sample(X)
        else:
                #分类每一样本   
                labels = []
                #X.shape[0]表示样本数
                for i in range(X.shape[0]):
                        #对于每一个样本给出一个判别的类别标签
                        label = self._predict_single_sample(X[i])
                        labels.append(label)
                return labels
            
if __name__ == '__main__':
    X = np.array([[1,1,1,1,1,2,2,2,2,2,3,3,3,3,3],
                 [4,5,5,4,4,4,5,5,6,6,6,5,5,6,6]])
    X = X.T
    y = np.array([-1,-1,1,1,-1,-1,-1,1,1,1,1,1,1,1,-1])
    
    nb = MultinomialNB(alpha=1.0,fit_prior=True)
    nb.fit(X,y)
    print (nb.predict(np.array([2,4])))
    #输出-1

朴素贝叶斯的优缺点

---

优点：

• 生成式模型，通过计算概率来进行分类，可以用来处理多分类问题。
• 对小规模的数据表现很好，适合多分类任务，适合增量式训练，算法也比较简单。

缺点：

• 对输入数据的表达形式很敏感。
• 由于朴素贝叶斯的“朴素”特点，所以会带来一些准确率上的损失。
• 需要计算先验概率，分类决策存在错误率。

朴素贝叶斯理论推导与三种常见模型
通俗易懂！白话朴素贝叶斯
数据挖掘（8）：朴素贝叶斯分类算法原理与实践
算法杂货铺——分类算法之朴素贝叶斯分类(Naive Bayesian classification)

---

scikit-learn对于各种贝叶斯分类器有着很好的支持，只需要几行代码就可以用于处理自己的数据，下面通过一个简单的文本分类的例子来看一下。

• 首先导入所选的包

from pprint import pprint
from time import time

from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfTransformer, TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn import metrics

from sklearn.metrics import accuracy_score,f1_score

• 加载数据，这里选择的20newsgroups。20newsgroups包含18000篇新闻文章，一共涉及到20种话题，数据集分为两部分：训练集和测试集。
  sklearn中有两个对应的API进行调用：
• sklearn.datasets.fetch_20newsgroups(data_home=None, subset=‘train’, categories=None, shuffle=True, random_state=42, remove=(), download_if_missing=True, return_X_y=False)
  • data_home:指定数据集下载路径
  • subset：“train”、“test"或"all”
  • categories:指定选择的类别
  • shuffle
  • random_state
  • remove:去除’header’,‘footers’,'qutoes’中的内容，防止分类模型过拟合
  • download_if_missing：是否需下载数据
  • return_X_y
• sklearn.datasets.fetch_20newsgroups_vectorized

categories = ['alt.atheism', 
              'talk.religion.misc',
              'comp.graphics', 
              'sci.space']
# 加载数据集
newsgroups_train = fetch_20newsgroups(subset='train',categories=categories)
print("%d documents" % len(newsgroups_train.filenames))
print("%d categories" % len(newsgroups_train.target_names))
print()

• 加载分类器

vectorizer = TfidfVectorizer()
vectors = vectorizer.fit_transform(newsgroups_train.data)
clf = MultinomialNB(alpha=.01)
clf.fit(vectors, newsgroups_train.target)

• 预测

newsgroups_test=fetch_20newsgroups(subset='test',categories=categories)
vectors_test=vectorizer.transform(newsgroups_test.data)

pred=clf.predict(vectors_test)
print(f1_score(newsgroups_test.target,pred,average='macro'))
print(accuracy_score(newsgroups_test.target,pred))