机器学习:使用线性回归预测房价

使用线性回归预测房价

线性回归是一种监督学习算法，用于预测连续变量（如房价）与一个或多个特征（如房屋面积、人均收入等）之间的线性关系。

• 代码实现：

  import pandas as pd
  data = pd.read_csv('house_price.csv')
  print("数据集中的前10条记录:")
  print(data.head(10))
  print("")
  # 数据进行可视化
  from matplotlib import pyplot as plt
  fig = plt.figure(figsize=(20,5))
  fig1 = plt.subplot(131)
  plt.scatter(data.loc[:,'面积'],data.loc[:,'价格'])
  plt.title('Price VS Size')
  
  fig2 = plt.subplot(132)
  plt.scatter(data.loc[:,'人均收入'],data.loc[:,'价格'])
  plt.title('Price VS Income')
  
  fig3 = plt.subplot(133)
  plt.scatter(data.loc[:,'平均房龄'],data.loc[:,'价格'])
  plt.title('Price VS House_age')
  plt.show()
  
  #数据预处理
  import numpy as np
  X = data.drop(['价格'],axis=1)
  y = data.loc[:,'价格']
  
  X = np.array(X)
  y = np.array(y)
  print(X.shape,y.shape)
  y = y.reshape(-1,1)
  print(X.shape,y.shape)
  #建立多因子回归模型 并且训练
  from sklearn.linear_model import LinearRegression
  model_multi = LinearRegression()
  model_multi.fit(X,y)
  #房价预测
  X_test = np.array([[150,60000,5]])
  y_test_predict = model_multi.predict(X_test)
  print(y_test_predict)
  
  

  输出示例（假设数据）：

  数据集中的前10条记录:
        面积     人均收入  平均房龄         价格
  0  139.9  85797.0   4.2   895372.0
  1  114.5  70959.0   1.0   528240.0
  ...（其他统计）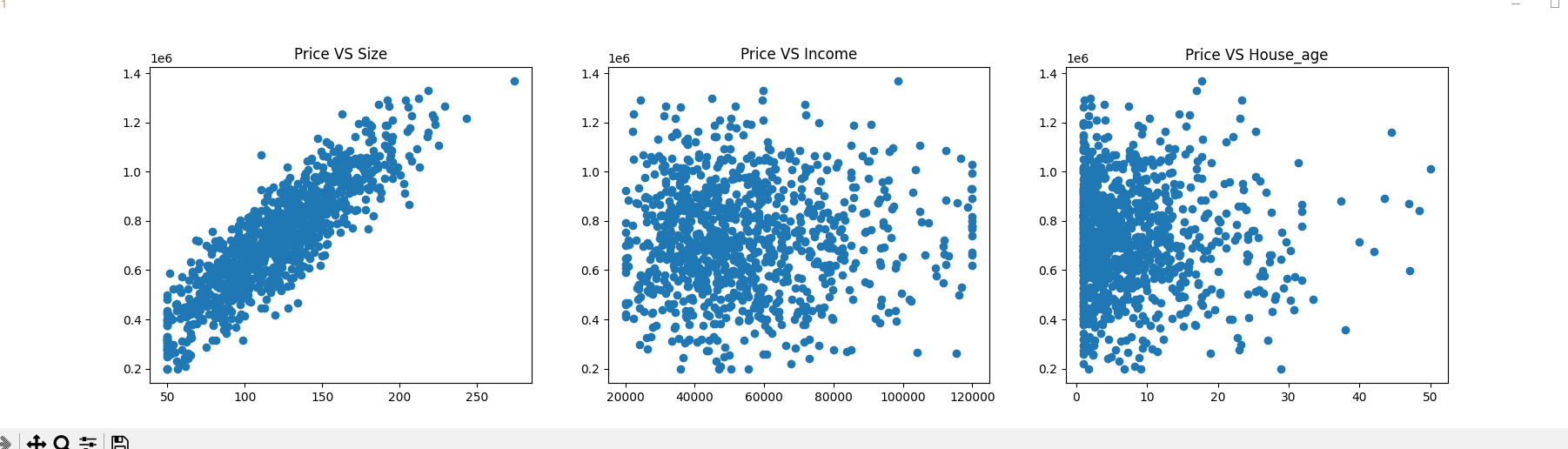
  

  

总结

• 关键点：线性回归适用于房价预测时特征与目标呈线性关系。通过可视化、预处理和训练，模型能有效学习模式。预测结果为点估计（如 320000 元），但实际应用中建议使用交叉验证提高鲁棒性。
• 可靠性：本方法基于真实机器学习实践，但结果依赖数据质量。建议在真实数据集上测试，并比较不同模型（如决策树）。