浅析光无源器件通光孔径与光束尺寸的关系

添加图片注释，不超过 140 字（可选）

光通信的飞速发展正驱动着带宽需求的指数级增长。作为构建光网络物理层连接的基石，无源器件的性能，哪怕是最细微的提升，都深刻影响着整个系统的稳定与效率。从数据中心的高速互连到5G前传的可靠链路，低损耗、高稳定性已成为无源器件毋庸置疑的刚性需求。

深入剖析影响无源器件性能的核心要素，最终往往会聚焦于一个物理层面的关键指标：光的耦合效率。而在决定这一效率高低的诸多参数中，通光孔径（Aperture） 扮演着极其核心却又充满设计挑战的角色。

添加图片注释，不超过 140 字（可选）

▍通光孔径：定义与工程意义 ▶

通光孔径，需从光学原理与工程实践的双重维度来精准理解。它指的是光无源器件（如准直器、隔离器、WDM等）中，能够有效传输光信号的径向空间范围。具体而言，它表现为器件内部光学元件（如透镜、滤光片、光纤端面等）允许光束通过的最大物理孔径尺寸（通常指直径或半径）。

需要强调的是，通光孔径并非一个简单的几何尺寸参数。它与传输光束的能量分布特性深度绑定 —— 其设计目标必须确保有效覆盖光束能量的主要承载区域，方能最大限度减少光信号在传输过程中的损耗。

▍高斯光束特性与孔径损耗模型 ▶

在光通信器件中，光传输普遍遵循高斯光束模型。其横截面上的光强分布可表示为：

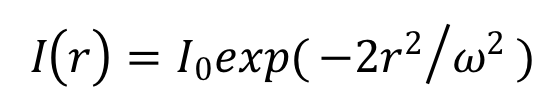
添加图片注释，不超过 140 字（可选）

其中：

◈ I0是光束中心处的峰值光强

◈ r是距离光束中心的径向距离

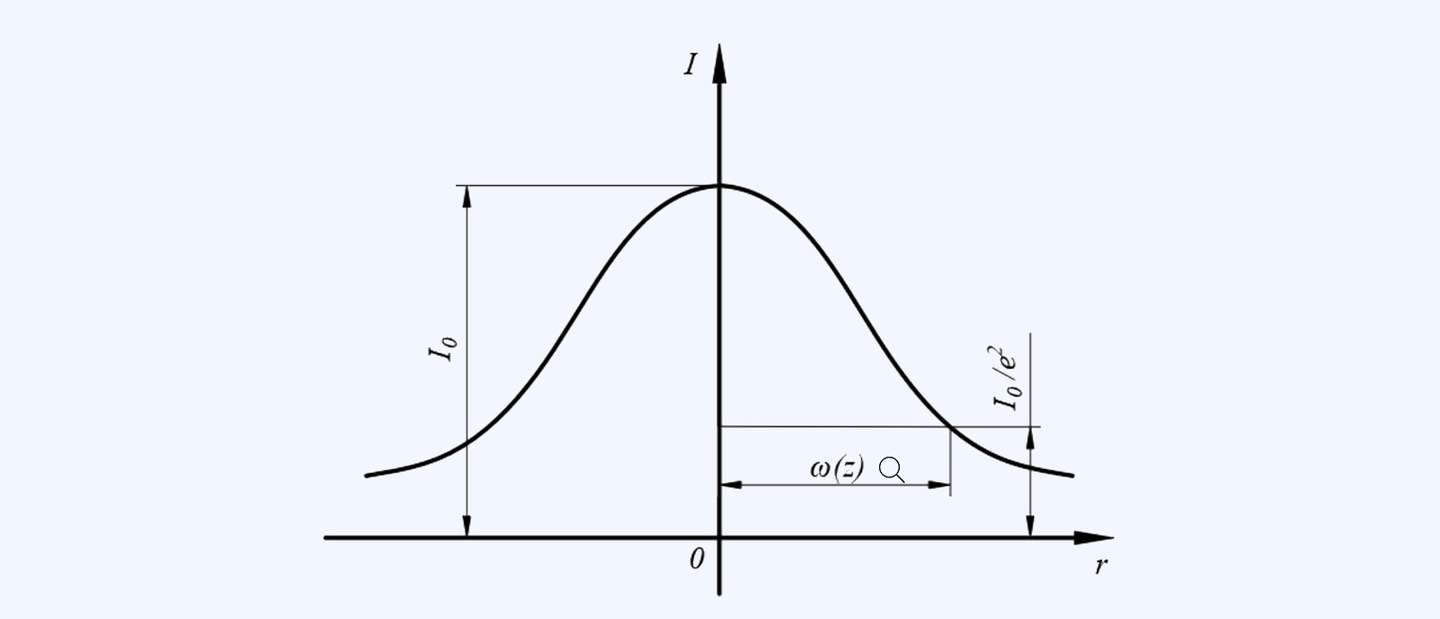
◈ ω是光束的特征半径（通常定义为光强降至中心峰值I0的 1/e^2 ≈13.5%时的半径）。

下图展示了典型高斯光束的能量分布：

添加图片注释，不超过 140 字（可选）

计算半径为r的圆形区域内所包含的光能量占总能量的比例𝞰，需对光强在该区域内进行积分：

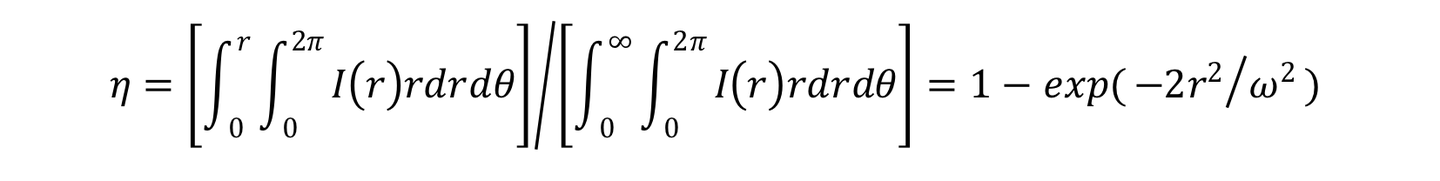
添加图片注释，不超过 140 字（可选）

由此，因通光孔径限制（孔径半径 R）而引入的插入损耗（Insertion Loss, IL）可表示为：

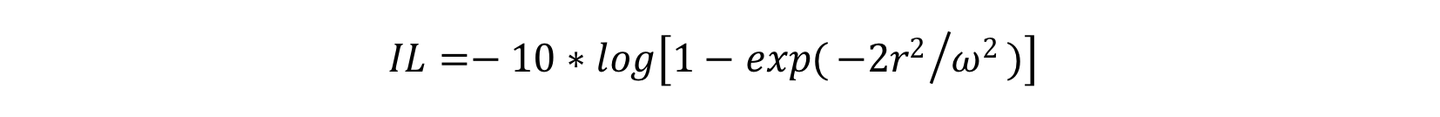
添加图片注释，不超过 140 字（可选）

下图清晰展示了损耗 IL与比值r/ω的关系

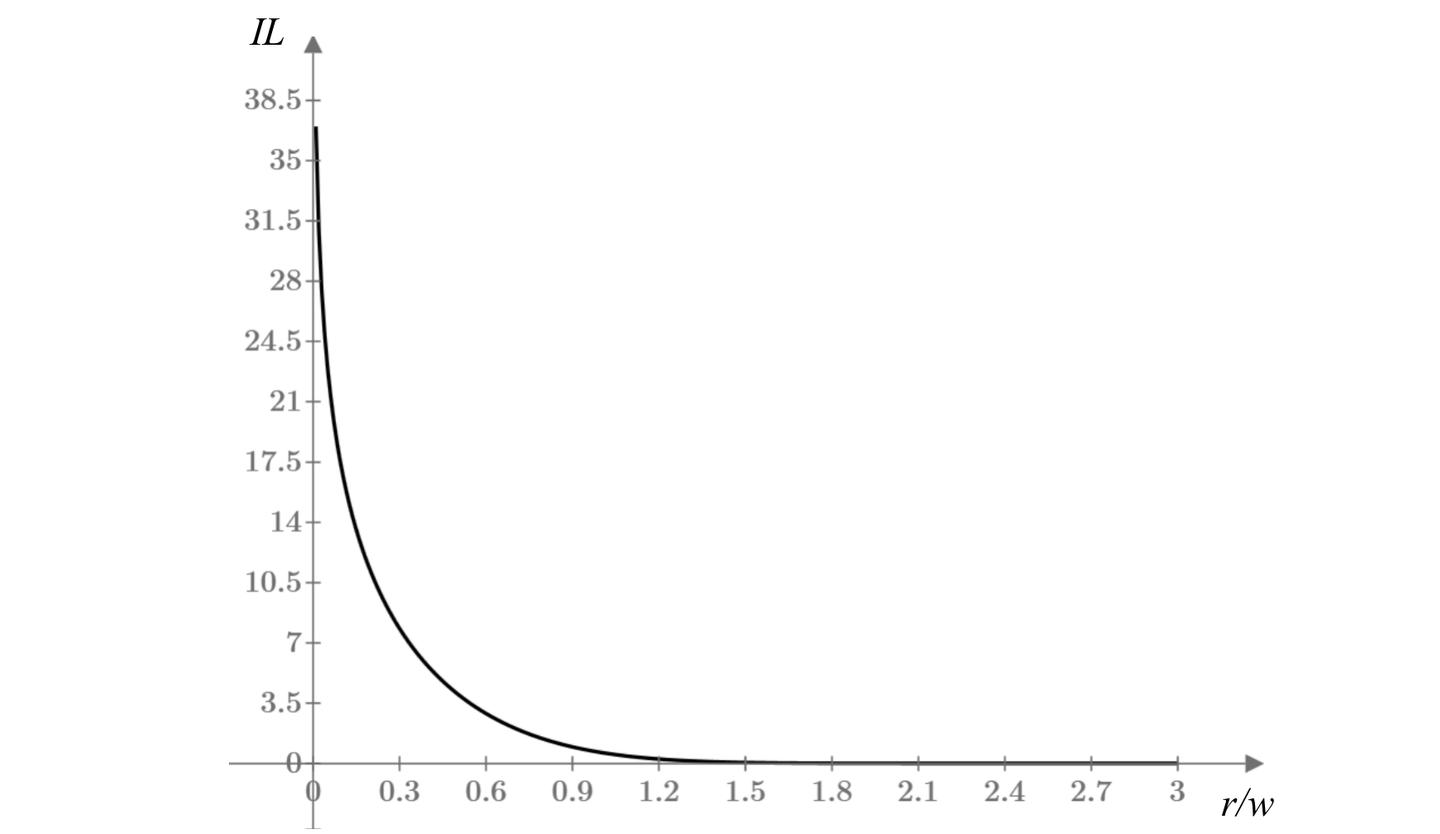
添加图片注释，不超过 140 字（可选）

▍关键设计准则与工程实践 ▶

由上述模型和图表可得出关键结论：

◈ 当 r/ω = 1（即通光孔径直径D=2R=2ω）时，孔径限制引入的损耗约为 0.63 dB。

◈ 当 r/ω = 1.5（即通光孔径直径D=3ω）时，损耗显著降低至 0.05 dB。

◈ 当 r/ω = 1.75（即通光孔径直径D=3.5ω）时，损耗进一步降至 0.01 dB。

◈ 当 r/ω = 2（即通光孔径直径D=4ω）时，损耗已低至 0.001 dB，在绝大多数应用场景中可忽略不计。

因此，在产品结构设计中，一个重要的设计准则是：将通光孔径（直径）设定为不小于光束特征半径ω的4倍（即 D= 4ω）。此时，由孔径限制带来的损耗几乎可以忽略（~0.001 dB）。

当然，实际工程应用还需严谨考虑：

1. 制造公差与装配精度： 材料的尺寸公差、元件的装配误差要求在设计时预留额外余量。

2. 系统整体约束： 器件或模块的整体尺寸可能有限制。

▍为何不追求“光强为零”的边界？ ▶

工程设计中不追求包含“所有”光能量的无限大孔径，原因有二：

1. 物理探测极限： 实际探测器的灵敏度有限，无法区分强度极弱的光信号与环境背景噪声。

2. 数学理论限制： 高斯光束的光强 I(r)随着 r 增大而渐近趋近于零 (当 r→∞, I(r) → 0)，但永远不会在有限距离处严格等于零。理论上“光强为零”的位置位于无穷远处，包含“全部”能量需要无限大空间，这在物理系统中无法实现。

▍飞宇的工程智慧与解决方案 ▶

飞宇光纤深谙通光孔径设计与光束控制的精妙平衡对器件性能的决定性影响。当产品整体尺寸受限，留给通光孔径的余量紧张时，飞宇通过优化透镜参数（如焦距、曲率） 来主动缩小光束特征半径ω，从而在有限的物理空间内满足 D=4ω的设计准则，确保器件达到低损耗、高性能的要求，完美契合用户对产品功能和结构的需求。

添加图片注释，不超过 140 字（可选）